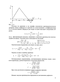Содержание к диссертации
Введение
Глава 1. Обзор и анализ литературных источников по теме исследования 6
1. Классические модели теории запасов 6
1. Управление запасом при детерминированной постоянной интенсивности спроса...6
2. Однопродуктовая модель с постоянной интенсивностью спроса и поставок 7
2. Обзор современных результатов 9
1. Моделирование двух стратегий в системе управления запасом со случайными задержкой и спросом 9
2. Стохастическая модель управления запасом с учетом портящихся товаров 11
3. Стохастические модели управления запасом с непрерывным пуассоновским спросом для функционала средних затрат в условиях наличия дисконта 13
4. Математическая модель управления запасами при случайном сезонном спросе и ненадежных поставщиках 14
5. Определение вероятностных характеристик полумарковских моделей с положительным и отрицательным сносами 16
6. Краткие обзоры современных результатов 18
Глава 2. Управление запасом непрерывного продукта с прекращением потребления на время поставки 23
1. Модель регенерации с мгновенным пополнением запаса 23
1. Постановка задачи и параметры модели 23
2. Необходимые результаты из теории дробно-линейных функционалов 24
3. Определение функционала затрат 27
4. Постановка экстремальной задачи 28
5. Существование и единственность решения 29
6. Случай линейных функций затрат 33
7. Анализ функционала прибыли и линейных затрат 35
8. Исследование функционала прибыли при наличии затрат на пополнение запаса.. 39
9. Интегральная прибыль 44
2. Модель регенерации со случайным временем задержки поставки 45
1. Постановка задачи и параметры модели 46
2. Определение функционала затрат 47
3. Постановка экстремальной задачи 49
4. Существование решения 50
5. Случай линейных функций затрат 53
6. Исследование функционала прибыли и линейных затрат 55
7. Интегральная прибыль 60
3. Расчет оптимальных управлений для некоторых числовых примеров 61
Глава 3. Модели с непрерывным потреблением продукта 78
1. Управление запасом непрерывного продукта в модели с детерминированной
задержкой поставки 79
1. Описание математической модели 79
2. Оптимальное управление по функционалу средних удельных затрат 80
3. Случай линейных функций затрат и линейной функции задержки поставки 85
4. Анализ функционала прибыли 86
5. Линейный вариант задания основных характеристик модели 91
6. Экспоненциальные функции цены и линейные затраты при линейной задержке... 95
7. Постоянная функция задержки 96
8. Продолжение потребления и случайная задержка 97
2. Управление запасом непрерывного продукта в модели с непрерывным потреблением при наличии дополнительных затрат с детерминированной задержкой поставки 100
1. Результаты для общих функционалов 100
2. Оптимальное управление в линейном варианте модели 107
3. Оптимальное управление при линейных затратах и фиксированной длительности задержки 112
3. Расчет оптимальных параметров управления для некоторых числовых примеров. 126
Заключение 132
Список литературы 133
- Математическая модель управления запасами при случайном сезонном спросе и ненадежных поставщиках
- Случай линейных функций затрат
- Случай линейных функций затрат и линейной функции задержки поставки
- Управление запасом непрерывного продукта в модели с непрерывным потреблением при наличии дополнительных затрат с детерминированной задержкой поставки
Введение к работе
Объект исследования и актуальность темы. Работа посвящена исследованию нескольких стохастических моделей управления непрерывным запасом в схеме регенерации.
По мере развития экономических и торговых взаимоотношений все большую актуальность приобретают логистика и оптимальное управление имеющимися ресурсами или продуктами. Принятие верных управляющих решений при выработке стратегии управления запасом является важным условием эффективного функционирования торгового предприятия. Для разработки управляющих решений необходим математический анализ исследуемой системы, позволяющий получить научно обоснованные теоретические рекомендации.
В настоящем исследовании предлагается рассмотреть ряд математических моделей функционирования товарного склада, на котором хранится непрерывный продукт. В роли такого продукта могут выступать нефть, горюче-смазочные материалы, газ, вода, зерно и т. п. Экономика России сейчас сильно зависит от экспорта нефти и газа, что определяет значимость исследования подобной тематики. Кроме того, поставки указанных продуктов имеют большое значение и на внутреннем рынке. Таким образом, существует объективная необходимость в исследовании такого рода моделей.
Кроме того, предложенные математические модели могут быть рекомендованы к использованию в крупных торговых сетях, где при большом объеме запасов хранящиеся продукты удобно описывать непрерывными параметрами.
Предметом исследования являются экстремальные задачи для функционалов, описывающих эффективность систем управления запасом.
Теоретико-методологические основы управления запасами разрабатывались многими отечественными и зарубежными учеными и практиками. Еще в начале XX века появился ряд статей по определению оптимального объема заказа - Ф. Харриса (1913г.), К. Андлера (1929г.) и Р. Уилсона (1934г.). В последние десятилетия вопросами управления запасами занимались такие отечественные ученые как: Т.А. Алиева, Б.А. Аникин, Е. В. Булинская, A.M. Гаджинский, К.В. Инютина, В.А. Лотоцкий, СР. Микитьянц, Ю.М. Неруш, Г.Б. Рубальский, Ю.И. Рыжиков и др.; зарубежные ученые Е. Копытов, П. Зермати, М.Р. Линдере, Х.Е. Фирон, Т.Л. Саати, А. Прабху, Д. Хедли, Т. Уайтен и др.
Общая характеристика полученных результатов. В первой главе диссертации дан краткий обзор ряда современных результатов в исследуемой области. На его основе можно сделать ряд общих выводов, относительно характера этих результатов. В первую очередь необходимо отметить, что в большинстве рассматриваемых моделей поиск решения проводится не аналитическими, а численными методами. Далее, почти во всех исследованиях случайные характеристики моделей представлены не произвольными, а заданными законами распределения. В большинстве случаев потребление продукта описывается пуассоновским процессом. В
качестве функционалов, характеризующих эффективность управления системами, как правило, выступают средние общие затраты, или, реже, общая прибыль.
Модели, рассматриваемые в настоящем исследовании, имеют целый ряд существенных отличительных особенностей. Исследование предложенных моделей будет проводиться аналитическими методами, численные примеры будут приведены для иллюстрации полученных результатов. Математической моделью функционирования системы является регенерирующий процесс.
Роль параметра управления играет время от момента очередного пополнения запаса до момента следующего заказа на пополнение запаса. При этом параметр управления имеет случайный характер, а проблема оптимизации управления заключается в определении вероятностного распределения, доставляющего экстремум заданному функционалу - показателю качества. Оптимизация осуществляется по множеству распределений неотрицательных случайных величин. Показателями качества управления являются стационарные функционалы, выражающие средние удельные затраты или среднюю удельную прибыль, связанные с функционированием данной системы. Длительность задержки поставки может быть как случайной, так и детерминированной; при этом ее характеристики зависят от объема потребленного продукта.
Цель диссертационной работы заключается в получении условий на характеристики системы, при которых существует оптимальная стратегия управления запасом, а также соотношений для ее определения в каждой из рассматриваемых моделей.
Научная новизна работы. В диссертации получены следующие новые научные результаты, связанные с управлением запасом непрерывного продукта.
Для каждой из трех основных видов моделей управления, рассмотренных в диссертации, доказаны теоремы о существовании оптимальных детерминированных значений параметра управления и получены соотношения для определения этих оптимальных значений.
Проанализирован целый ряд частных случаев основных вариантов моделей, связанных с конкретными предположениями о характеристиках системы. Для вариантов, в которых стоимостные характеристики модели являются линейными, получены явные аналитические формулы для оптимальных значений параметров управления.
Проведено численное исследование значительного числа теоретических примеров, иллюстрирующих полученные общие результаты. В каждом их этих примеров исследовано поведение зависимостей основных показателей качества от параметров управления.
Научная и практическая ценность. Результаты диссертации могут представлять интерес для специалистов, занимающихся приложениями теоретико-вероятностных методов в экономических, технических и других областях. Они также могут быть использованы в качестве теоретической основы для будущих исследований более сложных систем управления запасами.
Личное участие автора. В совместно выполненных научных работах [2, 5-7] вклад каждого из соавторов может быть определен следующим образом. Научному руководителю диссертации Шнуркову П.В. принадлежит разработка основной математической модели управления запасом, получение представлений для исследуемых функционалов, постановки соответствующих экстремальных задач и формулировки основных теорем о существовании оптимальных значений параметров управления. Автору диссертации принадлежат аналитические преобразования и выводы, содержащиеся в доказательствах основных утверждений, аналитические исследования теоретических примеров, а также численное исследование примеров, иллюстрирующих полученные теоретические результаты.
Апробация работы. Результаты работы были представлены на следующих научных конференциях и симпозиумах:
IX Всероссийский симпозиум по прикладной и промышленной математике (весенняя сессия) (Кисловодск, 2008 г.);
Седьмая Международная Петрозаводская конференция "Вероятностные методы в дискретной математике" (Петрозаводск, 2008 г.);
Научно-техническая конференция студентов, аспирантов и молодых специалистов Московского государственного института электроники и математики 2005, 2007 и 2008 годов.
Кроме того, результаты работы докладывались на заседаниях следующих научно-исследовательских семинаров:
Научный семинар кафедры теории вероятностей Российского университета дружбы народов;
Научный семинар по теории запасов Института проблем управления имени В.А. Трапезникова Российской Академии наук.
Публикации. Результаты диссертации опубликованы в 7 работах соискателя, список которых приведен в конце автореферата. Научные работы [2, 5, 6, 7] опубликованы в журналах, входящих в утвержденный ВАК перечень ведущих рецензируемых научных изданий, в которых должны быть размещены основные научные результаты диссертации на соискание ученой степени кандидата наук. При это работы [2] и [5] представляют собой развернутые научные статьи, включающие подробное изложение и обоснование полученных результатов. В указанных публикациях содержатся все основные результаты диссертации.
Структура и объем диссертации. Диссертация состоит из введения, трех глав, заключения и библиографии. Объем работы составляет 135 страниц текста, в том числе 132 рисунка. Библиография включает в себя 36 наименований, в том числе и публикации диссертанта по теме исследования. Каждая глава разбита на параграфы, параграфы, кроме посвященных числовым примерам, в свою очередь, разбиты на пункты, имеющие порядковую нумерацию. Формулы внутри каждого пункта имеют тройную нумерацию с указанием на параграф и номер пункта; при ссылке на формулы из другой главы номер главы указывается отдельно. Рисунки также имеют тройную нумерацию с указанием на параграф и номер пункта.
Математическая модель управления запасами при случайном сезонном спросе и ненадежных поставщиках
В работе [9] на примере торговой деятельности посреднической фирмы строится модель управления запасами и осуществляется поиск оптимальной стратегии поведения, гарантирующей фирме получение наибольшей прибыли при заданном уровне обслуживания, учитывая все особенности ее потребителей, поставщиков и рынка, на котором она работает. Рассматриваемая система управления запасами является стохастической системой с периодическим контролем уровня запасов, случайным нестационарным спросом и поставками, распределение которых зависит от величины поданного заказа в соответствующий источник пополнения запаса. В работе представлены результаты численного исследования предложенной авторами модели. Фирма должна разработать календарную программу формирования запасов угля на предстоящий период планирования. В качестве критерия оптимальности управления, т.е. выбора размера заказа, используются полные ожидаемые издержки в течение всего периода планирования. Перечислим особенности структуры управления запасами на фирме. 1. Фирма осуществляет периодический контроль за уровнем запасов и ежемесячно пополняет свои запасы, оформляя заявку на поставку угля, раз мер которой зависит от уровня запасов на начало текущего месяца, предпо лагаемой величины суммарного спроса до конца периода планирования и ожидаемой величины поставки. 2. Величина реального спроса становится известной только после оформления заказа на поставку угля. Этот спрос по возможности удовлетво ряется за счет созданных запасов, при дефиците неудовлетворенный спрос откладывается и удовлетворяется за счет последующих поставок. 3. Фирма имеет несколько постоянных источников пополнения запасов.
При планировании заказов по предприятиям-поставщикам необходимо учитывать реальные возможности и надежность каждого поставщика. 4. Поставки по каждому заказу, независимо от предприятия-поставщика, осуществляются в течение месяца по предварительной договоренности о сроках поставки с каждым поставщиком. 5. Стоимость одной тонны угля не зависит от предприятия-поставщика и включает в себя транспортные расходы, связанные с перевозкой груза по железной дороге. 6. Делая заказ на поставку угля, фирма должна учитывать пропускную способность железной дороги, объем площадки в речном порту, которая арендуется фирмой для хранения угля, и суточную способность речного порта к принятию груза, так как в случае несвоевременной разгрузки вагонов фирма платит железной дороге довольно большой штраф за простой вагонов. Цель фирмы - разработать стратегию управления запасами, при которой минимизируется общая сумма ожигаемых затрат, связанных с поступлением угля в речной порт, омертвлением капитала в запасах и штрафом за отложенный спрос, а спрос удовлетворяется в соответствии с принятым уровнем обслуживания потребителей. При описании математической модели использовались следующие обозначении: і, — уровень запаса на начало отрезка t, который может принимать отрицательные значения при наличии отложенного спроса; yt - нестационарная неотрицательная дискретная случайная величина, характеризующая спрос на уголь на отрезке t=(t—l, t), где t = \,T; у,— прогнозные значения спроса на уголь на отрезке t; Xt = [Xt (&)=] - вектор заказов, поданных в период t, где Xt(k)— заказ к-му поставщику в период t. Так как объем поставки случаен и зависит от размера поданного заказа конкретному поставщику, введен вектор неотрицательных дискретных случайных величин Xt 0: X, =\xt(k)\=l— вектор поставок, где случайная величина Xt(k) характеризует объем поставки в период t к-и поставщиком и описывается условным распределением р{х(к) \ X, (к)). .
Состояние запаса угля на складе описывается стохастическим разностным уравнением: В качестве целевой функции используется сумма ожидаемых на каждом отрезке планирования затрат всех видов. Предусмотрены следующие затраты: Ъ — издержки, связанные с выполнением заказа; h — показатель, связанный с замораживанием денежных средств, вложенных в одну тонну угля; с — штраф за нехватку единицы продукта в течение одного промежутка времени между двумя последовательными шагами, (b, h, с — постоянны в течение всего периода планирования). Явный вид целевой функции записан ниже. \Xt) определяется следующей формулой: С учетом ограничений на объем склада, емкость железнодорожного вагона, пропускную способность порта в период t и желаемого уровня обслуживания построена допустимая область управлений. На основании принципа оптимума Беллмана записано рекуррентное соотношение динамического программирования для нахождения оптимальной стратегии, которая минимизирует построенную целевую функцию. В работе [1] исследована модель управления запасами, в которой пополнения и спросы осуществлялись последовательно, а в модели, рассматриваемой в данном разделе, спрос может произойти после одной или нескольких поставок. Эта модель была исследована в монографии [3]. Приступим непосредственно к изложению модели. Пусть некий склад в начальный момент имеет запас товара, равный z 0 . За случайное время 5 на склад со скоростью tga (0 а 90) поставляется товар случайного размера и размер товара становится равным z + ,. Затем он переходит в режим подготовки приема товара длительностью случайного времени rj]. Далее либо с вероятностью Р{д = 0} = 1 - р осуществляется пополнение товара и он переходит в состояние z + + 2 , либо с вероятностью Р{д Щ-р со скоростью tgfi (0o J3 90) переходит в состояние max(0, z + , - д ) и т.д. Предполагается, что размер поставки , длительность запаздывания щ и размер спроса д - взаимно независимые одинаково распределенные случайные величины: & (), гі, 0, j 0, i,j=l,2,... Аналитический вид процессаXj(t), построенного на основе этих вероятностных предположений задан в работе [2]. Одна из реализаций процесса X(t) , полученного из Xj(t) задерживанием его в нуле методом Боровкова, показана на рис. 2.51.1.
Случай линейных функций затрат
Данные функции затрат удовлетворяют условиям теоремы 1.5.1. Действительно, cj(x), с2(х) - дифференцируемые, неотрицательные функции, С](х) возрастает, определена для х 0, cj(x)=0 для х 0; с2(х) убывает, определена для х 0, с2(х)=0 для х 0; cj(0)=c2(0)=0. Hm с2(х) = lim (- sx) = +оо. По Х- -со X— -со кажем, что решение экстремальной задачи (1.4.2) существует и единственно, и найдем его в явном виде. Выражение (1.5.1) примет вид Очевидно, что знак f(u), являющейся производной целевой функции в (1.4.2), на каждом из двух интервалов совпадает со знаком соответствующего выражения в круглых скобках в (1.6.3). Рассмотрим эти выражения отдельно. О Следовательно, fi(u) (значит, и производная целевой функции) отрицательна для 0 и т/а и сама целевая функция строго убывает на этом интервале. Как видно из характера графика, /г(и) (следовательно, и производная целевой функции) отрицательна для т/а и щ и положительна для и0 и со, в точке т/а равна нулю. Значит, целевая функция имеет глобальный минимум в точке щ, щ - положительное решение уравнения (1.6.4). Решение уравнения (1.6.4) дается следующей формулой: a V s Таким образом, в случае функций затрат вида (1.6.1), (1.6.2) необходимо т /р + S пополнять запас продукта на складе через время, равное и0 = —. . a V s Убедимся, что полученное решение, согласно утверждению 1.5.1, удовлетворяет неравенству т/а щ и , где и - решение уравнения (1.5.6). Действительно, рт=-я(т-аи ) 7. Анализ функционала прибыли и линейных затрат
В условиях предыдущей модели дополнительно предположим, что от реализации хранящейся продукции склад получает доход, равный D(z)=zg-z, где z - объем реализованной продукции, g 0, z 0. Тогда, с учетом скорости реализации а 0, получаем, что условный доход на интервале регенерации (при условии, что длина интервала rj= t) D(t) = х ga t, если 0 t a T gx, если — t oo. a Тогда математическое ожидание дохода на одном интервале между моментами регенерации от D(G(-))= \D{t)dG(t). о Выберем в качестве функционала удельную среднюю прибыль на периоде регенерации: Q0 со $D(t)dG(t)- JA(t)dG(t) n(G(-)) = -2 , \tdG(t) о где A(t) определена в (1.3.3). Поставим экстремальную задачу следующим образом: со оо \D(t)dG(t) - JA(t)dG(t) II(G(-)) = - тах, (1.7.1) \tdG{t) о где Л - некоторое множество функций распределения, на которых определен функционал IJ(G(-)). Воспользовавшись, как и ранее, теоремой для дробно-линейного функционала в (1.7.1) мы получаем, что, если существует максимум функционала в (1.7.1), то он достигается на некоторой вырожденной функции распределения: 00 со \D{l)dG(t)-\A{t)dG(t) maxil(GQ) = max-2 - = max il(GQ) = max (и) (м) , \tdG(t) о гдеЛ - множество вырожденных функций распределения (1.2.1). Таким образом, для решения исходной экстремальной задачи (1.7.1) необходимо решить задачу с. .de D(u)-A(u) п „ОЛ S(u) = —— -- max . (1.7.2) и иє(0,х) Заметим, что при 0 и т/а —— — = — = ga —. и им и Как было показано в теореме 1.5.1, функция — - убывает по и на и 0 и т/а, т.е. функция ga — возрастает и максимум S(u) на 0 и т/а не и достигается. Рассмотрим случай линейных функций затрат (1.6.1), (1.6.2). Теорема 1.7.1 Пусть функции затрат имеют вид (1.6.1), (1.6.2). Тогда решение экстремальной задачи (1.7.2) задается следующими формулами: при 0 g — максимум функции S(u) достигается в точке 2а U=jl Гт2 , 2gT j — (p + s)--s \az а у и/?и g —— в точке и= т/а. 2а Доказательство: Целевая функция в (1.7.2) для т/а и со примет вид /a t T/ /a gx - J р(т - ax)dx - j s(x - ax)dx u S(u) T , . asu2 gx (p + s) + SXM 2a 2 - = max u rx , иє[-;со) a Вычислим производную целевой функции: 2 2 х , . asu (1.7.3) fi?M u2 Исследуем знак числителя в (1.7.3) для т/а и со; 1)
Пусть — (р + s)- gx 0, т. е. 2а g -L(p + s). (1.7.4) 2а Тогда существует точка щ - положительное решение уравнения (1.7.5). _L2(p + s).gT_ l = 0. (1.7.5) 2a 2 Явная формула решения (1.7.5) имеет вид /1(42 2gx u0 = J" 2-(P + s)--= sla2 a а) Рассмотрим случай щ т/а. Л Определим условия, при которых выполняется это соотношение: ( т 2 2gx (p + s) а а и0 = а рт 2а g (1.7.6) С учетом (1.7.4) и (1.7.6) получаем общее условие, при котором имеет место случай 1а): рт 2а g График числителя в (1.7.3) для случая 1а) показан на рис. 1.7.1. и т/а хщ О Рис. 1.7.1 Так как знак числителя в (1.7.3) совпадает со знаком производной функции S(u) при т/а и со, то график целевой функции выглядит, как показано на рис. 1.7.2. ад т/а щ Рис. 1.7.2 и Как видно из рис. 1.7.2, максимум функционала (1.7.2) при 0 g 2а достигается в точке u0 = J Ґт2 2gx l а а —-(р + 8)--2- . б) Рассмотрим теперь вариант щ т/а, тогда рт 2а g С учетом (1.7.4) и (1.7.7) имеем общее условие на случай 16): - g —(p + s). 2а 2а График числителя в (1.7.3) для случая 16) изображен на рис.1.7.3. (1.7.7) и Рис. 1.7.3 Тогда график целевой функции в (1.7.2) выглядит, как показано на рис. 1.7.4. Рис. 1.7.4 рт Т. е., при — g —(p + s) максимум функционала (1.7.2) достигается 2а 2а в точке и=т/а. 2) Пусть теперь — (p + s) - gx 0, т. е. 2а (1.7.8) g (P + s). 2а Ha рис. 1.7.5 изображен график числителя в (1.7.3), соответствующий случаю 2). и Рис. 1.7.5 Из рис. 1.7.5 видно, что, как и в случае 16), при т/а и х функция S(u) убывает, и при g — (p + s) максимум функционала (1.7.2) также дос 2а тигается в точке и= т/а. Таким образом, при 0 g — максимум функционала достигается в а si а 1 fт2 , , 2gx точке u0 =,-—(p + s) \ , при g —— в точке и=т/а. 2а 8. Исследование функционала прибыли при наличии затрат на пополнение запаса В предыдущей задаче предположим, что стоимость заказа сз=у-к2, у 0, h - размер заказа. Тогда, с учетом скорости реализации а 0, получаем, что условный доход на интервале регенерации (при условии, что длина интервала ц = t) ga, і если 0 t —, a gr, Xесли — t oo . a D(t) = Тогда математическое ожидание дохода на одном интервале между моментами регенерации определяется следующей формулой. D(G(-))= \D(t)dG(t). о Выберем в качестве функционала удельную среднюю прибыль на периоде регенерации: 00 СО \D{t)dG{t) - j(A(t) + y(at)2) /G(/) nc(G(-)) = 4 , jtdG(t) о где A (t) определена в (1.3.3). Поставим экстремальную задачу следующим образом: со со \D(t)dG(t)- j(A(t) + j(at)2)dG(t) ne(G(-)) = і мпах, (1.8.1) tdG(t) о \tdG(t) где Л - некоторое множество функций распределения, на которых определен функционал nc(G(-)). Воспользовавшись, как и ранее, теоремой для дробно-линейного функционала в (1.8.1), мы получаем, что если существует максимум функционала в (1.8.1), то он достигается на некоторой вырожденной функции распределения: СО СО maxnc(G(.)) = max = max ПС(С(-)) = 0()єЛ G(-)eA G(-)eA JD(t)dG(t) - j(A(t) + y(at)2)dG(t) _о 00 jtdG(t) D(u) - A(u) - y(au)2 = max —— — — , мє(0;оо) и где A - множество вырожденных функций распределения (1.2.1). Таким образом, для решения исходной экстремальной задачи (1.8.1) необходимо решить задачу
Случай линейных функций затрат и линейной функции задержки поставки
В условиях предыдущей модели дополнительно предположим, что от реализации хранящейся продукции склад получает доход. Пусть цена единицы продукции в момент времени t определяется следующей функцией: х g,(r-crt), если 0 t + h(ot) Pit) = (1.4.1) g2 (г - at), если — t + h(ort) ад, a где величина x-at представляет собой количество продукта, имеющегося на складе в момент времени t (или его нехватку при отрицательном значении). Тогда доход от реализации продукции со склада на интервале между моментами регенерации, при условии, что заказ на поставку производится через время t, выражается следующей формулой: т a t+h(at) t+h(at) a J g, (г - ax)dx, 0 t + h(at) D(t + h(at)) = (1.4.2) a fg r - ax)dx + а Г g2(r -ax)dx, — t + h(crt) ад. о v a Математическое ожидание дохода на одном интервале между моментами регенерации есть СО C(G(-)) = J (t + h(at))dG(t). (1.4.3) о Выберем в качестве функционала удельную среднюю прибыль на периоде регенерации: СО со j)(t + h(at))dG(t) - $A(t + h(at))dG(t) П(вО) - = - max, (1.4.4) j(t + h(at))dG(t) где A(t+h(at)) определена в (1.2.1), Л - некоторое множество распределений неотрицательных случайных величин, на которых определен функционал ЩО(-)). Как и ранее, воспользовавшись теоремой об экстремуме дробно-линейного функционала, получаем, что если существует максимум функционала (1.4.4), то он достигается на некоторой вырожденной функции распределения: max n(G(-)) = max U(G(-)) = max S((), (1.4.5) G(-) sA G(-)eA f 0 где A - множество вырожденных функций распределения, а функция S(t) определяется соотношением, записанным ниже. t+b(at) t+h(at) a fg1(x-ax)dx- jc, (x - ax)dx — 7IT f:0 t + h(at) ±., S(t) = t + h(at) a /a t+h(cA) % t+h(at) # JSi(T" «x) c + a jg2( - ax)dx - \c1 (x -ax)dx - jc2(x- ax)dx r: — t + h(at) 00. 0 Va X . x t + h(at) a Докажем следующее фундаментальное утверждение о характере решения экстремальной задачи управления запасом по отношению к функционалу прибыли.
Теорема 1.4.1 Пусть ci(x), С2(х), gi(x), g2(x) - неотрицательные дифференцируемые функции, С](х) не убывает, определена для х 0, cj(x)=0 длях 0; с2(х) не возрастает, определена длях 0, с2(х)=0 длях 0, с2(0)=0; gi(x) не возрастает, определена для х є [О, т), g2(x) не убывает, определена для х є(- х , 0], gi(0)=g2(0)—g 0, g(0) eR, h(oct) - неубывающая неотрицательная дифференцируемая функция от t, h(0)=0. Пусть также limc2(x) = +oo, limg2(x) = g( \g(_) 0. Тогда: решение экстремальной задачи (1-4.4) по отношению к функции S(t) существует и удовлетворяет уравнению Уа t+h(at) ag2 (х - a(t + h(at))) (Г + /z(at)) - a Jgj (т - ax)dx - fg2 (т - ax)dx о у /a Va. t+h(at) -c2(x-a(t + h(«t)))-(r + /2(at))+ Jcj(x-ax)dx+ Jc2 (x - ax)dx = 0. (1.4.6) о у /a причем данное решение принадлежит интервалу t: — t + h(at) 00; a если лее функция c2(x) или функция g2(x) является строго монотонной (убывающей или возрастающей соответственно), то функция S(t) имеет единственную экстремальную точку — глобальный максимум. Доказательство: Рассмотрим интервал t: 0 t + h(at) —. a t+h(at) t+h(m) a jg,(x-ax)dx- jcj(x-ax)dx S(t) = - . t + h(cA) Заметим, что при доказательстве теоремы 1.2.1 уже проводилось исследование аналогичных функционалов. Как было показано, выражение не возрастает при t: 0 t+h(at) T/a. Можно показать, что ана / + h(cd) отрицательной, невозрастающей дифференцируемой функции gi(x). Действительно, (t+h(at) Л t+h(at) (1 + ah (cd)) [g, (T - a(t + h(at))) (t + h(cd)) - Jg, (г - ax)dx] t+h(at) jc,(T-ax)dx t + h(at) логичное выражение d_ dt Jg,(x-ax)dx t + h(cd) t+h(at) a Jg1(x-ax)dx В си не убывает при t: 0 t+h(at) r/a для не (t + h(at))2 лу геометрического смысла интеграла и свойств функции gj(x) выражение в квадратных скобках неотрицательно (см. рис. 1.4.1). gj (x-a(t+h(at))) gi(T-ax) О t+h(at) х Рис. 1.4.1 С учетом того, что функция h(at) не убывает, получаем, что t+Цса) d_ dt 0, Jg!(x-ax)dx t + h(a\) Продолжим исследование функции S(t).
Исходя из проведенного анализа характера функций, стоящих в числителе функции S(t), можно сделать вывод, что исследуемая на экстремум функция S(t) не убывает на интервале t: 0 t+h(at) r/a, и максимум S(t) следует искать при t: — t + h(at) ад . a Рассмотрим множество значений параметра t, удовлетворяющих этому условию. При t: — t + h(crt) оо уа a t+h(at) r+A(at) a Jgi(T-ax)dx + cc \g2(T-ax)dx- Jc1(x-ax)dx- jc2(T-ax)dx 5(/) = t + h(cd) Вычислим производную / [(1 + ahXat)) ag2 (x - g(t + h(crt))) - (1 + ah (at))c2 (x - a(t + h(at)))]- (t + h(cd)) (t + h(at))2 У t Уа t+h(at) (l + ah (at)) a JgjCr - ax)dx + a [g2(r - ax)dx - jc, (x-ax)dx - jc2(x -ax)dx 0 i/ 0 x/ /a /a (r + /2(crt))2 Отсюда получаем, что необходимое условие экстремума запишется здесь следующим образом: [ag2 (х - a(t + h(at))) - с2 (т - a(t + h(at)))] (t + h(c&)) Уа (+A(at) Уа t+h(at) -a \gx(r - ax)dx - а щ2(т - ax)dx + c1(T-ax)dx+ jc2 (x - ax)dx = 0 , О т/ 0 "/ /a /a или, что то же самое, Уа t+h(at) «g2 (х - a(t + h(at))) (t + h(ai)) - or Jgx (r - crt)c& - a Jg2 (r - at)ce t+h(at) c2 (x - a(t + h(at))) (ґ + h(c&)) - jc, (x - ax)dx - Jc2 (x - ax)dx = 0. Обозначим L(t) левую часть последнего уравнения. Заметим, что знак функции L(t) при t: — t + h(crt) оо совпадает со знаком функции S t). а Рассмотрим функцию Уа t+h(at) F(t) = c2(x-a(t + h(crt)))-(f + /z(at))- jc,(x-ax)dx- jc2(x-ax)dx, входящую в вы о у /а ражение для L(t). Заметим, что данная функция уже исследовалась в ходе доказательства теоремы 1.2.1. Тогда она обозначалась B2(t), но в данном случае нам будет удобнее использовать другое обозначение. Обозначим дополнительно через F(t) выражение в квадратных скобках. Как было установлено, функция F(t) на интервале t: — t + h(ert) oo не убывает, F(t0) 0, где a t0 : t0 + h(crt0) = — и limF(t) = +a . a - » Введем в рассмотрение еще одну функцию def У "«at) E(t) = org2 (х - a(t + h(at))) (t + h(at)) - a J g, (r - aK)dx - a J g 2 (r - ax)dx. Таким обра зом, имеет место соотношение L(t) = E(t)-F(t). Исследуем поведение функции E(t). Вычислим производную данной функции и определим ее знак. Е (0 = -a2g2 (х - a(t + h(at))) -(1 + ah (at)) (t + h(at)) + a{\ + ah (at)) g2 (x - a(t + h(at))) --ag2(x-a(t + h(at)))-(l + «h ))=-a2g2(x-a(t + h(at)))-(l + ahXat))-(r + /2(at)) 0.
Управление запасом непрерывного продукта в модели с непрерывным потреблением при наличии дополнительных затрат с детерминированной задержкой поставки
Ранее, при исследовании моделей в 1, 2 главы 2 и 1 главы 3, издержки системы складывались из затрат, связанных с хранением положительного уровня запаса на складе, и затрат, связанных со штрафами за нехватку продукции на складе. Естественно предположить, что в системе могут возникнуть другие затраты, связанные, например, с платой за пополнение уровня запаса или с расходами по транспортировке. Данный параграф будет посвящен проблеме управления запасом непрерывного продукта при непрерывном потреблении в условиях наличия дополнительных затрат. 1. Результаты для общих функционалов В условиях модели, изложенной в 1, дополнительно предположим, что в системе возникают дополнительные затраты, связанные со оплатой заказанной продукции. Разумно потребовать, что данные затраты будут зависеть от объема заказа на поставку, т. е. от количества потребленного к моменту заказа продукта. Пусть функция сз(х) задает затраты на заказ партии продукта размером х единиц в единицу времени. Функция общих затрат на интервале регенерации (под общими затратами понимаются суммарные затраты, связанные с хранением продукта и дефицитом) представляется (2.1.3) Как и в предыдущих моделях, минимум данного функционала изначально ищется среди всевозможных неотрицательных распределений. Однако эта задача, как и ранее сводится к поиску оптимальных вырожденных случайных распределений, т.е. к решению следующей экстремальной задачи: Заметим, что функция I(t) задается различными аналитическими выражениями в двух областях возможных значений аргумента t. Данные области определяются .
Поскольку функция Hat), определяющая длительность задержки поставки, в дальнейшем предполагается неубывающей и непрерывной, функция t + h(at) является монотонно возрастающей и непрерывной при всех t 0. Если h(0)- limh(A) —, то существует единственная точка t0, удовлетворяющая соотношению t0 +h(ax0) = —. Именно эта точка разделяет две указанные выше a области з Пусть функция сз(х) задает затраты на заказ партии продукта размером х единиц в единицу времени. Функция общих затрат на интервале регенерации (под общими затратами понимаются суммарные затраты, связанные с хранением продукта и дефицитом) представляется (2.1.3) Как и в предыдущих моделях, минимум данного функционала изначально ищется среди всевозможных неотрицательных распределений. Однако эта задача, как и ранее сводится к поиску оптимальных вырожденных случайных распределений, т.е. к решению следующей экстремальной задачи: Заметим, что функция I(t) задается различными аналитическими выражениями в двух областях возможных значений аргумента t. Данные области определяются . Поскольку функция Hat), определяющая длительность задержки поставки, в дальнейшем предполагается неубывающей и непрерывной, функция t + h(at) является монотонно возрастающей и непрерывной при всех t 0. Если h(0)- limh(A) —, то существует единственная точка t0, удовлетворяющая соотношению t0 +h(ax0) = —. Именно эта точка разделяет две указанные выше a области значений аргумента t, в которых функция Ці) задается различным образом. Сформулируем и докажем основное теоретическое утверждение, характеризующее область поиска решения экстремальной задачи (2.1.3). Пусть cj(x), С2(х), сз(х) - неотрицательные дифференцируемые функции, С](х) не убывает, определена для х 0, С](х)=0 для х 0; С2(х) не возрастает, определена для х 0, с2(х)—0 для х 0; с3(х) не убывает, определена для х 0, сз(х)=0 для х 0; h(at) - неубывающая неотрицательная дифференци руемая функция от t, причем /г(0) = lim h(A)
Предположим далее, что вы д-»+о а полнены следующие условия: lim с2(х) = +оо, и существует такое число t\ tn, X-»o , t + h(cd) что функция —— является монотонно неубывающей при t tl. jc3 (ax)dx о Обозначим через t\ /0 такое значение параметра t, что с2 (т - a(t + h(at)) с, (т) при t t\. Тогда функция I(t) достигает глобального минимума в некоторой точке t=t, принадлежащей замкнутому начений аргумента t, в которых функция Ці) задается различным образом. Сформулируем и докажем основное теоретическое утверждение, характеризующее область поиска решения экстремальной задачи (2.1.3). Пусть cj(x), С2(х), сз(х) - неотрицательные дифференцируемые функции, С](х) не убывает, определена для х 0, С](х)=0 для х 0; С2(х) не возрастает, определена для х 0, с2(х)—0 для х 0; с3(х) не убывает, определена для х 0, сз(х)=0 для х 0; h(at) - неубывающая неотрицательная дифференци руемая функция от t, причем /г(0) = lim h(A) —. Предположим далее, что вы д-»+о а полнены следующие условия: lim с2(х) = +оо, и существует такое число t\ tn, X-»o , t + h(cd) что функция —— является монотонно неубывающей при t tl. jc3 (ax)dx о Обозначим через t\ /0 такое значение параметра t, что с2 (т - a(t + h(at)) с, (т) при t t\. Тогда функция I(t) достигает глобального минимума в некоторой точке t=t, принадлежащей замкнутому конечному интервалу значений параметра t, 0 t t o, где величина t 0 t0определяется соотношением t 0 = тах(ґ, , t 2).3ua чение t является корнем уравнения t+h(at) (1 + ah (ot))[c, (т - a(l + h(at))) (/ + h(at)) - сг (т - ax)dx] + t+h(at) + (1 + ah (at)) [c3 (a(/ + h(at)))(f + h(at)) - j c3 (ax)dx + jc3 (ax)dx] - c3 (at) (t + h(cd)) = 0, если о о 0 t t0, либо удовлетворяет уравнению