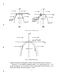Содержание к диссертации
Введение
Глава I. Траектории-утки в многомерных сингулярно возмущенных системах с одной быстрой переменной
1. Постановка задачи 13
2. Доказательство теоремы 18
Глава II. Решения многомерных сингулярно возмущенных систем, не являющиеся утками
1. Вспомогательные утверждения 29
2. Доказательство основных результатов 33
Глава III. Некоторые случаи вырождения
1. Возмущение исходной системы 46
2. Рождение двух траекторий-уток из одной 50
Глава IV. Случай нескольких быстрых переменных
1. Постановка задачи 60
2. Доказательство теоремы 65
Заключение 77
Список литературы 78
- Доказательство теоремы
- Вспомогательные утверждения
- Возмущение исходной системы
- Рождение двух траекторий-уток из одной
Введение к работе
В данной работе исследуется поведение решений сингулярно возмущенных систем обыкновенных дифференциальных уравнений. Система обыкновенных дифференциальных уравнений называется сингулярно возмущенной, если ее можно представить в виде
EX = f(xty,t,E), X Є Я"\
У = 9(x,V,t,), У Є Rn,
где 0 < є <С 1, fi{x,y,tt0) — 0(1) при є —> 0, і ~ 1,... , m, а точка обозначает производную по времени t. Очевидно, что такие системы не удовлетворяют условиям теоремы о непрерывной зависимости решения от параметра, а значит, их надо рассматривать отдельно. При изучении сингулярно возмущенных систем возникает множество интересных явлений. Их легко проиллюстрировать на примере уравнения Ван-дер-Поля, которое можно представить в следующем виде:
єх-у- f(x) = F(x,у), у- -{х + a) = G(x,у), х,у Є R, (1)
где точка обозначает производную по времени, є - малый параметр, а - числовой параметр. Считаем, что график функции f(x) имеет вид, сходный с кубической параболой и выполнены свойства /(0) = 0, f'{x) > О при х > 0 и х < -1, f{x) < 0, при х Є (-1,0), /"(-1) < 0, /"(0) > 0, что соответствует показанному на рис. 1.
Естественно называть переменную х быстрой переменной, а переменную у - медленной, так как в каждой точке (х*,;у*) фазовой плоскости, в которой выполнено |^(а;*,у*)| > q > 0, где q — некоторая константа, не зависящая от є, вектор фазовой скорости будет иметь вид (F(x*,yJ)/e, (?(*,у*)). Таким образом, при малом значении є вектор фазовой скорости практически параллелен оси х, то есть происходит почти мгновенное перемещение вдоль нее.
Положим є = 0. Тогда система (1) превратится в вырожденную систему
F(x,y)=0,y = G(x,y). (2)
Из первого уравнения системы (2) получим уравнение у = f(x), которое определяет так называемую кривую медленных движений, а именно кривую, в є— окрестности которой значение фазовой скорости каждой из переменных имеет порядок единицы. На рисунке 1 изображена кривая
* / y=f(x)
* /v
-e W
0 x
Рис. 1: Кривая медленных движений у = /(х).
медленных движений и показано, как направлены векторы фазовой скорости системы в различных частях фазовой плоскости. Глядя на рисунок сразу становится понятно, почему участки F~ — {{х,у) : F(x,y) = О, F'x(xi у) < 0} и F+ ~ {(х, у) : F(x, у) = 0, Ffx{x, у) > 0} медленной кривой называются устойчивым и неустойчивым участками соответственно.
Итак, система (1) имеет единственное положение равновесия (—а, /(—а)), которое, очевидно, асимптотически устойчиво при а<0иа>1и неустойчиво при а Є (0,1) для любого фиксированного значения є > 0. Кроме того, известно, что данная система имеет устойчивый предельный цикл при а Є [а, 1 — Ь], где а, Ь > 0, а < 1 — Ь. Возникает вопрос, каким образом из асимптотически устойчивого положения равновесия при а < 0 возникает при увеличении а предельный цикл.
В 1978 году этим вопросом занимались французские математики Фран-син Диенер и Марк Диенер. Они исследовали данную систему методами нестандартного анализа и обнаружили появление нового вида траекторий, которые они назвали траекториями-утками (см., например [1], [2]).
Итак, механизм возникновения предельного цикла из положения равновесия показан на рисунке 2: от а) до г). Интервал изменения параметра о, на протяжении которого происходит это "перерождение", очень мал
Рис. 2: Появление предельного цикла из положения равновесия: а) асимптотически устойчивое положение равновесия; б) утка без головы; в) утка с головой; г) предельный цикл.
и составляет величину порядка е~к^ для некоторого к > 0 при є —> О (см., например [3], [4]), Промежуточные траектории (рис. 2 б)-в)) и есть траектории-утки.
Определение. Траекторией-уткой сингулярно возмущенной системы дифференциальных уравнений называется траектория, которая, попав в малую (порядка є) окрестность устойчивой части кривой медленных движений, сначала продолжает двиокение вдоль нее, затем переходит в малую окрестность неустойчивой части кривой медленных движений и некоторое время находится в этой окрестности так, чтобы в обоих случаях проходилось расстояние порядка единицы.
Действительно, на рис. 2 б)-в) видно, что траектории проходят как вдоль устойчивого участка F", так и вдоль неустойчивого участка F+. Само же название "траектория-утка" появилось благодаря внешнему виду цикла, изображенного на рис. 2 в). Подрисовав "глазик" и "лапки" мы получим нечто, похожее на летящую утку.
Но не стоит думать, что траектории-утки — это некоторое специфическое явление, для обнаружения которого требуются неимоверные усилия. Наличие таких траекторий можно заметить в самых простых системах.
Пример. Рассмотрим систему
єх' - х2 + у, х,у Є Л, ^
у' — а — х, a = const. ^ '
Здесь кривая медленных движений — обычная парабола у = —х2, одна часть которой (при х < 0) устойчива, а другая (при х > 0) - неустойчива. Направление векторов фазовой скорости на самой кривой медленных движений зависит от значения параметра а.
Рассмотрим траекторию [x(t),y{t)) системы (3), проходящую через точку (жо,уо)ї ^0 < min(0,a), — х% < yQ < 0. Исследуем поведение этой траектории. Очевидно, что сначала происходит быстрое падение на устойчивую часть кривой медленных движений (см.рис.3 а)-б)). Изучив направления векторов фазовой скорости вблизи кривой медленных движений, логично было бы предположить, что сначала траектория проходит некоторое расстояние порядка единицы вдоль устойчивого участка кривой медленных движений, а затем, при а > 0 происходит "срыв" с кривой медленных движений вблизи точки (0,0) фазовой плоскости (см.рис. 3 а)), а при a < 0 траектория стремится к устойчивому положению равновесия (см.рис.З б)).
Рассмотрим систему (3) при a = 0. В этом случае удается найти
решение системы в явном виде. Итак, общее решение уравнения имеет
~х2 = Сехр(-2у/є)-у+є/2,
х = у = 0,
где С - произвольная постоянная. Полагая С = 0, получим траекторию-утку
у = -х2 + є/2,
движение по которой продолжается также и вдоль неустойчивой части
б
а)
б)
Рис. 3: а) а > 0: б) а < 0.
_ ^ y=-x2+s/2
Рис. 4: Траектория-утка.
кривой медленных движений, причем бесконечное время (см.рис.4).
Заметим, что из данного примера видно, что траектории-утки — это не всегда циклы, как это было в случае уравнения Ван-дер-Поля, и тем более они обычно не имеют форму "утки".
«
/
Итак, траектории-утки были найдены и продолжали изучаться с помощью нестандартного анализа ([5] — [7]). Но оказалось, что и другие методы применимы к этому явлению. Так, например, в работах [8] и [9] используется метод раздутия. Применение инструментов классического асимптотического анализа также дает хорошие результаты ([10] — [13]).
В данной работе изучение поведения траекторий сингулярно возмущенных систем опирается именно на методы классического асимптотического анализа. В первой главе исследуется система с одной быстрой и произвольным числом медленных переменных и с бесконечно гладкой правой частью
х = f(x, у), єу = д{х, у), х Є Пх С ІГ, у Пх С R, 0 < є < 1. (4)
Рассматривается случай пересечения корней вырожденного уравнения: п—мерные поверхности Гі — {(х, у) : у — <р(х)} и Г2 = {(х, у) : у — ф(х)} пересекаются по гладкой (п —1)—мерной поверхности / (см. рис. 5). Считаем, что все траектории вырожденной системы, лежащие на Гі, пересекают I общим образом в направлении из устойчивой части поверхности медленных движений в неустойчивую. Ставится вопрос, какие из траекторий вырожденной системы могут являться нулевым приближением траекторий исходной системы, то есть могут порождать траекторию-утку исходной системы.
В первой главе выводятся достаточные условия появления траектории-утки исходной системы из конкретной траектории вырожденной системы (обозначим ее х = Xo(t)) и показывается, что они зависят только от точки Xq пересечения выбранной траектории вырожденной системы с поверхностью /. Для этого вводится некоторая функция Ф(з), где х ~ -y(s) - гладкая параметризация поверхности I.
Итак, рассмотрим (п—1)—мерные поверхности 1~ и /+, проекции которых на поверхность Гі пересекают общим образом траекторию х = xa(t) вырожденной системы, проходящую через точку xq. Обозначим эти точки пересечения соответственно через х~ и х+ и возьмем такие у~ и у+, что [х~,у~) Є 1~ и (х+,у+) 1+. Предположим, что из точек (х~,у~) и (х+,т/+) происходит нужное падение (при t -) оо и t —> —со соответственно) на поверхность Г і (см. [14]).
Рассмотрим кривую L: состоящую из отрезков, соединяющих точки (х~:у~) и (х~,(р(х~)) и точки (х+,(р(х+)) и (х+,у+), и лежащего на Гі участка кривой (x0(t),
(см. рис. 7).
Теорема 1.1 из первой главы говорит о том, что при Ф($о) = О) УФ(зо) Ф 0, где so - значение параметра s, для которого xq — j(sq), существует (п — 2)—параметрическое семейство траекторий системы (4) такое, что для каждой траектории из этого семейства ее концы лежат на I' и 1+ соответственно, а ее нулевым приближением при є -> 0 является кривая L.
Вторая глава посвящена изучению ситуации, когда основное условие теоремы 1.1 на точку пересечения траектории вырожденной системы с поверхностью I не выполнено и исследуется поведение траекторий системы (4) в этом случае.
Рассмотрим кривую Z-2, состоящую из участка кривой L> лежащего между точками (х~,у~) и (хо,(р(хо)), и лежащего на Г^Г участка траектории системы
з:- /(х,ф{х)), у=:ф{х),
проходящей через точку (xq,
Из результатов теорем 2.1 - 2.4 следует, что в случае выполнения условия Ф(йо) > 0 нулевым приближением при є -> 0 траектории системы (4), проходящей через точку (х~,у~), является кривая L?..
Рассмотрим теперь кривую з, состоящую из участка кривой L, лежащего между точками (х~,у~) и {xq,
Суммарным результатом теорем 2.1, 2.2, 2.5, 2.6 является тот факт, что если Ф(^о) < 0, то нулевым приближением при є —)- 0 траектории системы (4), проходящей через точку (х~,у~), является кривая із-
Таким образом, главы I и II дают практически полное описание поведения траекторий системы (4) вблизи особенности (поверхности I) за исключением вырожденного случая Ф(яо) = 0, УФ(зо) = 0, из которого следует, что траектории-утки являются своего рода сепаратрисами, разделяющими два массива траекторий системы (4) с качественно различным поведением.
Отметим, что задачи, поставленные в первых двух главах диссертации, можно аналогичным образом рассматривать и в случае зависимости правой части системы (4) от малого параметра е. Но это немного усложнит выкладки и не позволит представить условия существования и несуществования траекторий-уток в таком простом и красивом виде, как для случая независимости правой части системы от є. Случай за-
висимости правой части системы от є представлен в первом параграфе третьей главы.
Стоит подчеркнуть, что основной проблемой при доказательстве теорем первых двух глав было исследование малой окрестности поверхности I, так как изучение поведения траекторий сингулярно возмущенных систем вдали от особенности было проведено еще до обнаружения такого явления как траектории-утки и полностью описано в [14]. Там показано, что вне любой не зависящей от є окрестности особой поверхности можно найти решение задачи Коши с нулевым приближением - траекторией вырожденной системы, если начальное условие удовлетворяет определенным требованиям. Случай пересечения корней вырожденного уравнения тоже изучался, но в основном для ситуации так называемого нормального переключения (см. [11]), то есть перехода траектории из малой окрестности устойчивой части одной поверхности медленных движений в малую окрестность устойчивой части другой поверхности медленных движений. Так, например, в статье [15] исследовалась ситуация, аналогичная рассмотренной в главах I и II, но изучался только тот случай, когда нулевым приближением траектории является кривая 2.
Следует отметить, что результаты первых двух глав являются обобщением на случай нескольких медленных переменных работы [16], в которой изучалось скалярное сингулярно возмущенное неавтономное дифференциальное уравнение, что равносильно рассмотрению автономной системы с одной быстрой и одной медленной переменной. Кроме того, для возникновения траектории-утки в такой ситуации необходимо ввести зависимость правой части системы от вспомогательного параметра. Здесь же мы избавляемся от такой необходимости за счет увеличения количества медленных переменных, а в случае п > 2 добиваемся появления целого семейства траекторий-уток с одним нулевым приближением.
Заметим, что к решению подобных задач можно подойти и с другой стороны, то есть не выделять траектории вырожденной системы, способные породить траектории-утки, а, воспользовавшись вспомогательным параметром, пытаться построить утку с любым выбранным нами нулевым приближением. Такой подход представлен, например, в работах [17], [18]. Кроме того, если считать вспомогательный параметр функцией медленного переменного, то можно построить целую поверхность, состоящую из траекторий-уток (см. [19], [20]).
Доказательство теоремы
Стоит подчеркнуть, что основной проблемой при доказательстве теорем первых двух глав было исследование малой окрестности поверхности I, так как изучение поведения траекторий сингулярно возмущенных систем вдали от особенности было проведено еще до обнаружения такого явления как траектории-утки и полностью описано в [14]. Там показано, что вне любой не зависящей от є окрестности особой поверхности можно найти решение задачи Коши с нулевым приближением - траекторией вырожденной системы, если начальное условие удовлетворяет определенным требованиям. Случай пересечения корней вырожденного уравнения тоже изучался, но в основном для ситуации так называемого нормального переключения (см. [11]), то есть перехода траектории из малой окрестности устойчивой части одной поверхности медленных движений в малую окрестность устойчивой части другой поверхности медленных движений. Так, например, в статье [15] исследовалась ситуация, аналогичная рассмотренной в главах I и II, но изучался только тот случай, когда нулевым приближением траектории является кривая 2.
Следует отметить, что результаты первых двух глав являются обобщением на случай нескольких медленных переменных работы [16], в которой изучалось скалярное сингулярно возмущенное неавтономное дифференциальное уравнение, что равносильно рассмотрению автономной системы с одной быстрой и одной медленной переменной. Кроме того, для возникновения траектории-утки в такой ситуации необходимо ввести зависимость правой части системы от вспомогательного параметра. Здесь же мы избавляемся от такой необходимости за счет увеличения количества медленных переменных, а в случае п 2 добиваемся появления целого семейства траекторий-уток с одним нулевым приближением.
Заметим, что к решению подобных задач можно подойти и с другой стороны, то есть не выделять траектории вырожденной системы, способные породить траектории-утки, а, воспользовавшись вспомогательным параметром, пытаться построить утку с любым выбранным нами нулевым приближением. Такой подход представлен, например, в работах [17], [18]. Кроме того, если считать вспомогательный параметр функцией медленного переменного, то можно построить целую поверхность, состоящую из траекторий-уток (см. [19], [20]).
Глава III диссертации посвящена изучению некоторых вырожденных случаев. Так, в первом параграфе рассматривается проблема возмуще ния правой части системы (4) на порядок є и показывается, что данное вмешательство "сдвигает" траекторию-утку вдоль поверхности I на расстояние порядка единицы, то есть если какая-то траектория вырожденной системы удовлетворяла условиям главы I и порождала траекторию-утку системы (4), то для возмущенной системы утку будет порождать уже другая траектория вырожденной системы, находящаяся от прежней на расстоянии порядка единицы.
Во втором параграфе рассматривается система (4) в случае п = 2 и при условии Ф(в0) - 0, Ф (б0) = 0, Ф"($о) ф 0 и показывается, что при определенных условиях одна траектория вырожденной системы может являться нулевым приближением сразу двух траекторий-уток исходной системы, тогда как в обычной невырожденной ситуации теорема 1.1 говорит о единственности траектории-утки (при п — 2) с конкретным нулевым приближением. Для этого вводится вспомогательный малый параметр и соответствующие результаты доказываются для вспомогательной возмущенной системы.
В главе IV рассматривается система с несколькими быстрыми и несколькими медленными переменными и изучается тот же вопрос возникновения траекторий-уток, что и в главе I. Здесь опять доказывается существование (п — 2)—параметрического семейства траекторий-уток исходной системы с конкретным нулевым приближением. Для этого снова вводится своя функция $(s), отражающая характер пересечения выбранной траектории вырожденной системы с особой поверхностью I. И опять значение этой функции в вышеупомянутой точке пересечения играет определяющую роль в появлении траектории-утки. Однако построение поверхностей / и /+, на которых лежат концы траекторий указанного семейства, существенно сложнее. Это связано с возникновением условной устойчивости поверхности медленных движений, то есть поверхность устойчива по нескольким быстрым переменным, а по остальным быстрым переменным она неустойчива. Строго это формулируется следующим образом.
Введем в рассмотрение матрицу G(x) = дд(х, р(х))/ду, где все обозначения те же, что в (4), но переменную у считаем векторной.
Опрделение. Поверхность у — (fi(x) называется устойчивой, если все собственные значения матрицы G{x) имеют строго отрицательные действительные части (в той области, где рассматривается система) и неустойчивой, если все собственные значения матрицы G(x) имеют строго положительные действительные части. Если же не которые собственные значения имеют строго отрицательные действительные части, а остальные — строго положительные, то тогда поверхность медленных движений называется условно устойчивой.
На этот случай теория, описанная в книге [14], говорит, что для нахождения решения системы с конкретным нулевым приближением вдали от особенности надо решать не начальную задачу, а краевую, то есть нельзя построить решение с нулевым приближением - траекторией, лежащей на условно устойчивой поверхности медленных движений, - с заданным начальным условием (см. также [21]). Таким образом, представленное в главе IV семейство траекторий-уток с концами на некоторых I" и 1+ является как обобщением на случай нескольких быстрых переменных результатов главы I, так и обобщением решения краевой задачи, описанной в [14], в случае прохождения траектории вблизи особой точки.
В главе IV использовалась та же техника доказательства, что и в главе I. Также, возможно применение принципа сведения для медленных интегральных многообразий, то есть поверхностей, состоящих из траекторий системы, лежащих в малой окрестности поверхностей медленных движений (см. [11], [22], [23]). Но и в этом случае сведение задачи к локальной необходимо.
Здесь, как и для системы с одной быстрой переменной, возможно использование вспомогательного параметра (или вспомогательной функции) для нахождения траекторий-уток с заданным нулевым приближением (см. [24], [25]).
Следует отметить, что идея построения целых поверхностей, состоящих из траекторий-уток, возникла в связи с требованиями практических задач. Оказалось, что траектории-утки находят свое применение в таких областях, как теория горения, химические и биологические процессы ([26] — [30]). Что касается данной диссертации, то здесь ставилась математическая задача рассмотрения сингулярно возмущенной системы в наиболее общем виде.
Вспомогательные утверждения
Для завершения обоснования теоремы остается совершить обратный переход от локальной постановки задачи к глобальной, а точнее говоря, продолжить доставляемое леммой семейство траекторий системы (1.19) по лентам у = Ні(х, є) и у = ( є) ДО пересечения с поверхностями 1 и 1+ соответственно. В результате получим (п — 2)— параметрическое семейство траекторий системы (1.1) с концами на / и 1+ и с требуемым нулевым приближением L. Теорема доказана.
Итак, теорема 1.1 дает достаточные условия возникновения траекторий-уток в многомерной системе. Отметим, что задачу, поставленную в теореме 1.1, можно аналогичным образом рассматривать и в случае зависимости правой части системы (1.1) от малого параметрам. Но это немного усложнит выкладки и не позволит представить условия существования траекторий-уток в таком простом и красивом виде, как для случая независимости правой части системы от є. Случай зависимости правой части системы от є представлен в первом параграфе третьей главы.
Как уже отмечалось ранее, существует другой подход в исследовании возникновения траекторий-уток. Если считать, что правая часть сингулярно возмущенной системы дополнительно зависит от некоторого вспомогательного параметра, то при соответствующем выборе значения этого параметра можно добиться появления траектории-утки рассматриваемой системы с наперед заданным нулевым приближением (см. [17]). Если же считать этот вспомогательный параметр гладкой функцией медленного переменного и малого параметра є, то можно обеспечить порождение траекторий-уток всеми траекториями вырожденной системы (см. [19]).
В нашем же случае, то есть при отсутствии вспомогательного параметра, явно указываются траектории вырожденной системы, которые обязаны порождать траектории-утки исходной системы. Следует подчеркнуть, что обойтись без вспомогательного параметра в правой части системы возможно лишь в многомерном случае, то есть когда имеется более одной медленной переменной. В противном случае для появления траектории-утки наличие вспомогательного параметра необходимо (см. [16]).
В данной главе продолжается рассмотрение системы (1.1). Предполагаем, что условия 1.1 — 1.3 остаются без изменений, то есть мы опять рассматриваем систему (1.1) в случае пересечения корней вырожденного уравнения (1.2) и предполагаем, что все траектории системы (1.3), лежащие на Гц, являются утками. Теорема 1.1 дает достаточные условия "выживания" уток вырожденной системы (1.3), то есть вырастания из них траекторий-уток исходной системы (1.1). Здесь будет изучаться вопрос, являются ли эти условия необходимыми и каково поведение траекторий не уток.
Напомним, что определяющим условием "выживания" траектории-утки системы (1.3) является условие на точку пересечения рассматриваемой траектории с поверхностью I пересечения корней вырожденного уравнения (1.2) —условие 1.4. Рассмотрим ситуацию, когда условие 1.4 не выполняется, а именно, имеет место Здесь функция Ф(э) определяется равенством (1.6), a SQ — значение параметра, согласно параметризации (1.5), отвечающее выбранной нами траектории системы (1.3). В совокупности с результатами Главы I мы получим практически полное представление о рассматриваемой особенности (за исключением вырожденного случая, который будет изучен в следующей главе). Итак, для исследования поставленной задачи целесообразно воспользоваться методом асимптотических представлений, для применения которого первоначально необходимо свести задачу к локальной. Для этого, как и в Главе I, рассмотрим поведение при увеличении t (t 0) произвольно выбранной нами траектории системы (1.1), начальные значения {х іУ ) которой при t — 0 лежат в области влияния устойчивой части поверхности медленных движений Г \ Это означает, что если у(т) — решение задачи "в быстром времени" г = t/є то выполняется предельное соотношение Таким образом, согласно результатам книги [14], сначала из области влияния Г происходит "падение" решения в малую (порядка є) окрестность поверхности Гі, а затем движение продолжается в этой окрестности примерно по закону (x(t),y(t)), t О, где y(t) = p{x(t))t a x(t) — решение задачи Коши Добавим, что в силу условия 1.3 решение данной задачи с течением времени пересекает общим образом проекцию поверхности / на подпространство у = 0 в некоторой точке XQ, для которой считаем выполненным неравенство Ф($о) ф 0 (напомним, что XQ = 7(5о), где х = ч{$) — параметризация поверхности I пересечения Г і и Гг). Итак, мы можем считать, что задача локализована в произвольной малой (не зависящей от е) окрестности точки (XQ, P(XO)). Для удобства проведения дальнейших выкладок систему (1.1) целесообразно привести в окрестности точки (хо,ір(хо)) к так называемой нормальной форме. Здесь мы воспользуемся нормальной формой, отличной от той, что была в Главе I. Это оказывается удобнее в силу свойств исследуемых решений системы (1.1). Без ограничения общности будем считать точку (XQ, р(%о))началом координат. Считаем, также, что д уУ(0,0) 0 и (V (0) — V (0), /(0,0)) 0. Выполним в системе (1.1) замены а остальные п — 1 переменных [v\,..., vn-i) выберем следующим образом. Фиксируем произвольно точку (x,ip(x)) и выпустим из нее траекторию (х(), ip(x(t))) вырожденной системы Таким образом, значение параметра s(x) однозначно определяет траекторию системы (2.3), лежащую на IV Перейдем в системе (2.3) к новым координатам (,v), тогда система для v примет вид и = 0, а интересующее нас решение системы (2.3), проходящее через точку (XQ, р(хо)), В новых координатах запишется следующим образом: Итак, запишем систему (1.1) в новых координатах (z ,v). Далее, возьмем за новое время, что возможно в силу условия 1.1 пересечения поверхностей р(х) и ф(х) общим образом. В итоге получим систему где 7 и Aj - гладкие (в малой окрестности начала координат) функции, и выполнено условие 7(0) 0,0) = 1. Заметим, что Ф(йо) = 0 = Ді(0, 0,0) = 1. Следовательно, мы будем изучать систему (1.1) при Аі(0,0,0) ф 1. Сделаем в системе (2.4) замены
Возмущение исходной системы
На первом этапе доказательства сведем задачу к локальной. Отметим, что в данной ситуации это представляет большую трудность, чем в случае одной быстрой переменной.
Итак, рассмотрим при t 0 пучок траекторий системы (4.1), начальные условия которых при t = 0 лежат на 1 (5 ) в некоторой малой окрестности U точки (х ,у ). Опишем поведение каждой из вышеупомянутых траекторий при увеличении t.
Обозначим через Щ проекцию U на подпространство у — 0. Согласно результатам [14] для любой точки х Є С/о и для любого набора и = («+1, Um) Є &2 существует единственная траектория системы (4.1) с краевыми условиями и нулевым приближением (xo{t)і tp{xo{t))) при :-)-0. Заметим, что значение qg можно выбрать так, чтобы точка (х , р(х 0)) попала в произвольную достаточно малую не зависящую от є окрестность точки (гсо, (р(хо)). Таким образом, для любого малого q qo мы можем построить ленту у — Н\{х, « , є), #2(2, и , 0) = р(х), состоящую из частей указанных траекторий системы (4.1), определенных на отрезке —t\ t q. Далее, рассмотрим малую окрестность V С 1 (5+) точки (ж+,у+). Обозначим через VQ проекцию V на подпространство у — 0. Аналогично, согласно результатам [14] для любой точки ж Є VQ и для любого набора и = (ui ,..., u Lj) С?]1" существует единственная траектория системы (4.1) с краевыми условиями и нулевым приближением (xo(t), p(xo(t))) при є — 0. Опять отметим, что значение до можно выбрать так, чтобы точка (:г+0, (р(х+0)) попала в произвольную достаточно малую не зависящую от є окрестность точки {xQ,tp(xo)). Таким образом, для любого малого q до мы можем построить ленту у = #2(х, и і є)] H2(x,u ,Q) — p(x)i состоящую из частей указанных траекторий системы (4.1), определенных на отрезке q t t2.
Тем самым, интересующая нас проблема сводится к локальному вопросу о нахождении в некоторой малой окрестности указанной точки траекторий системы (4.1), концы которых лежат на лентах у — Нх(х,и ,є) и у = Н2(х,и ,є). Следующий этап доказательства — приведение исходной системы (4.1) в окрестности точки (жо, (р(хо)) к так называемой нормальной форме. Сначала обратимся к условиям 4.1 и 4.2. В системе для у выделим линейную часть и положим z — у — ір(х). В итоге получим систему — матрица, состоящая из строк
Сделаем замену быстрой переменной z = Л(х)г, приводящую матрицу линейной части к действительным осям, и снова обозначим быструю переменную через z. Полученная система будет выглядеть следующим образом: а все собственные значения матриц Ck-i(x) и Cm_jt(x) отличны от нуля, а именно, собственные значения С -\{х) имеют строго отрицательные действительные части, а собственные значения Ст-ь(х) — строго положительные действительные части.
Для описания очередной замены переменных фиксируем произвольно точку х Є Clx и выпустим из нее траекторию системы (4.2), т.е. рассмотрим решение w(t, х) этой системы с начальным условием w(0, х) = х. Согласно условию 4.3 существует единственный момент времени to = to (х) (положительный при х Г " и отрицательный при х Є Гд), для которого w(to,x) Є IQ. Обозначим, далее, через s — s(x) значение параметра s, отвечающее точке w(to(x)tx), и перейдем в системе (4.2) к новым координатам (, v): где Є R, v Є і?1-1, a SQ — значение параметра s, соответствующее выбранной нами точке XQ Є IQ. В итоге рассматриваемая система преобразуется к виду а интересующее нас ее решение х xo(t) в новых переменных задается равенствами
Итак, выполним в системе (4.9) замену (4.10). В результате с учетом равенств (4.11) она примет вид где 7i и 72 - некоторые соответствующие гладкие вектор-функции, а функции D(,v), (, v,z) и Д(, и, z) получились соответственно из С(х), S(x,z) и -j4(x)(V(pi(a:),/(х - ф + я + Л Щх, А"1 p[x))A"l{x)z при указанной замене координат.
Отметим, что в силу локальности задачи система (4.13) рассматривается в некоторой достаточно малой окрестности начала координат, следовательно переменную в ней можно взять за новое врехмя (см. первое равенство (4.13)): а для гладкой функции P справедливо соотношение Для обоснования следующей замены переменных вспомним, что мы исследуем краевую задачу, т.е. ищем траектории системы (4.1) с концами на поверхностях (лентах) у Н\(х, ,и ,є) и у — Н2(х,и ,є). Данные поверхности построены таким образом, что в исследуемой нами окрестности точки (хо, f{xo)) они находятся на расстоянии порядка є от поверхности Г, т.е. в новых координатах, от поверхности z — 0. Поэтому целесообразно предварительно сделать в системе (4.14) замену z/є — z, в результате которой с учетом свойств функции Р она преобразуется к виду
Рождение двух траекторий-уток из одной
И наконец, подставляя в (4.36) равенство (4.34) и применяя к получившемуся уравнению теорему о неявной функции, однозначно определяем ограниченные функции 5{ 5\(е, 8\,..., 5„_і), S2 = 52(єу 8%,..., 5„_i). Из этого выражения видно, что оставшиеся п — 2 параметра ( ,см- (4-34)) мы можем выбирать произвольно, т.е. для склейки двух семейств решений (4.22) нам достаточно только одной степени свободы.
Обратимся к третьему и четвертому равенствам (4.33). Вектора и1 и и2 это (&— 1)—мерный и (т — к)—мерный вектора произвольных постоянных, которые возникают вследствие произвольности выбора и Є G и и Є G соответственно. Следовательно, на данном этапе мы имеем h{ = ti{v},u2), д1 = д{{и1,и2). Из уравнений (4.28), (4.29) и оценок (4.32) видно, что где д\ и 2 некоторые гладкие независящие от и1 и и2 вектор-функции. Таким образом, третье уравнение (4.33) имеет вид . Следовательно, по теореме о неявной функции вектора и1 и и2 определяются однозначно.
Для завершения доказательства теоремы остается совершить обратный переход от локальной постановки задачи к глобальной, а точнее говоря, продолжить доставляемое леммой семейство траекторий системы (4.16) по лентам у = Ні(х,и ,є) и у = Н2(х,и ,е) до пересечения с 1 (6 ) и 1+(5+) соответственно. В результате получим (п — 2)— параметрическое семейство траекторий системы (4.1) с концами на 1 и 1+ и с требуемым нулевым приближением L. Теорема доказана.
Отметим, что по сравнению с Главой I здесь пришлось производить склейку траекторий дополнительно еще в двух местах, что явилось следствием условной устойчивости поверхности медленных движений. А также построение лент Ні и #2 в связи с многомерностью быстрой переменной достаточно усложнилось.
При доказательстве теоремы 4.1 и леммы 4.1 также возможно применение принципа сведения для медленных интегральных многообразий, то есть поверхностей, состоящих из траекторий системы, лежащих в малой окрестности поверхностей медленных движений (см. [11], [22], [23]). Но и в этом случае сведение задачи к локальной необходимо.
Траектории-утки — это достаточно новая тема для исследования в математике. Следовательно, еще много вопросов не изучено, тогда как описание поведения решений сингулярно возмущенных систем при отсутствии особых точек на поверхности медленных движений довольно полно (см. [14]). Кроме того, уже сейчас траекториям-уткам находится применение в прикладных задачах (см. [26] — [30]). Отметим, что например в теории горения траектории-утки описывают некоторый пограничный процесс, при котором происходит медленное горение, не переходящее ни во взрыв, ни в затухание. Следовательно, это безопасный процесс, который можно контролировать, что является наиболее важным в прикладных задачах.
Итак, в настоящее время изучение траекторий-уток ведется сразу с двух сторон: как при исследовании математических моделей конкретных реальных процессов, так и чисто с теоретической точки зрения. Сами теоретические исследования проводятся также с помощью различных математических инструментов (нестандартный анализ, метод раздутия, асимптотические методы). Результаты данной работы носят теоретический характер и основаны на применении методов классического асимптотического анализа. В главах Г и ІГ была рассмотрена система достаточно общего вида с одной быстрой и произвольным числом медленных переменных и представлено необходимое и достаточное условие (за исключением вырожденного случая) рождения траектории-утки из заданной траектории вырожденной системы. Затем, для системы с двумя медленными переменными исследовался случай вырождения, который не рассматривался в первых двух главах, и изучалось влияние возмущения правой части системы на эффект возникновения траектории-утки. В четвертой главе проведено обобщение результатов первой главы (достаточное условие возникновения траектории-утки) на случай нескольких быстрых переменных.