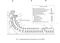Содержание к диссертации
Введение
Глава 1. Современное состояние моделирования тепломассообмена при обжатии металла 7
1.1. Теплофизические процессы при непрерывной разливке стали 7
1.2. Математические модели процесса непрерывной разливки 19
1.2.1. Основные виды применяемых математических моделей 19
1.2.2. Методы расчета процесса затвердевания слитка 24
1.3. Моделирование теплового состояния слитка 30
1.3.1. Методы решения задачи Стефана 30
1.3.2. Математические модели процесса затвердевания слитков 36
1.3.3. Влияние внешних воздействий на кристаллизующийся металл. 42
1.4. Инженерные расчеты теплофизических процессов при непрерывной разливке 57
1.4.1. Инженерный метод расчета затвердевания слитка 57
1.4.2. Инженерный метод расчета глубины жидкой фазы 63
1.5. Выводы по главе. Постановка задачи 66
Глава 2. Математическая модель процесса непрерывной разливки 70
2.1. Обобщенная схема обжатия слитка с жидкой сердцевиной 70
2.2. Математическая модель теплового состояния слитка 72
2.3. Результаты численного решения 80
2.3.1. Распределение температуры по сечению слитка 82
2.3.2. Динамика движения границы раздела фаз 86
2.4. Моделирование состояния двухфазной зоны 89
2.4.1. Скорости движения изотерм ликвидуса и солидуса 89
2.4.2. Динамика ширины двухфазной зоны 93
2.5. Результаты численного решения с учетом конвективных процессов 95
2.6. Тестирование модели и проверка на адекватность 98
2.7. Выводы по главе 105
Глава 3. Моделирование температурного поля в слитке с применением обжатия 107
3.1. Модель теплового состояния двухфазной зоны слитка при «мягком» обжатии 107
3.2. Результаты численного решения 111
3.3. Приближенный аналитический метод 115
3.3. Выводы по главе 133
Глава 4. Инженерный метод расчета обжатия слитка с жидкой сердцевиной 134
4.1. Фильтрация расплава в двухфазной зоне слитка 134
4.2. Методика расчета величины обжатия слитка 140
4.3. Выводы по главе 144
Заключение 145
Литература 146
- Основные виды применяемых математических моделей
- Инженерный метод расчета затвердевания слитка
- Результаты численного решения с учетом конвективных процессов
- Модель теплового состояния двухфазной зоны слитка при «мягком» обжатии
Введение к работе
Непрерывное литье стали является одним из наиболее прогрессивных технологических процессов, получивших в последние годы широкое распространение во всех развитых промышленных странах мира.
К основным преимуществам непрерывного литья следует отнести повышение качества и увеличение выхода годного металла, рост производительности труда, уменьшение капитальных затрат. Это создает предпосылки для развития способа непрерывной разливки и, как следствие, возникает необходимость рассмотрения и углубленного изучения теплофизических вопросов формирования слитка.
Экспериментальное изучение процесса затвердевания непрерывного слитка сопряжено с большими трудностями, несмотря на то, что в последнее время разрабатывается большое количество современного оборудования. В этих условиях значительную роль играют теоретические исследования. Основополагающими являются работы Г.П. Иванцова, А.И. Вейника, А.А. Скворцова, А.Д. Акименко, В.А. Ефимова, Ю.А. Самойловича, Б.Т. Борисова, Д.П. Евтеева.
Одной из главных теоретических и практических задач непрерывной разливки стали является совершенствование технологического процесса с целью получения более качественного продукта. Высокие требования, предъявляемые современной техникой к качеству стальных изделий, вызывают необходимость создания эффективных технологий кристаллизации сплавов.
Отличительными особенностями формирования непрерывного слитка, которые определяют его строение, являются большие скорости кристаллизации и малая продолжительность полного затвердевания. Вследствие этого, зональная ликвация в слитке значительно меньше, чем в обычном; но в осевой части слитка появляются ликвационные и усадочные дефекты, отрицательно действующие на качество получаемой заготовки. Известные методы внешнего воздействия, такие как холодильники, регулирование интенсивностью охлаждения, механическое перемешивание и др., не дают положительного результата для достижения поставленной цели — подавления процесса формирования ликвации и пористости в осевой зоне слитка.
В связи с этим в последнее время широкое распространение получила новая технология «мягкого» обжатия непрерывного слитка в неполностью затвердевшем состоянии, внедрение которой на МНЛЗ позволяет в значительной степени снизить количество осевых дефектов и, тем самым, улучшить качество готового продукта. К настоящему времени проведено достаточно большое количество исследований процесса «мягкого» обжатия: получено теоретическое обоснование режимов обжатий, созданы математические модели затвердевания непрерывных слитков, разработаны инженерные методы определения основных параметров обжатия. Тем не менее, многие аспекты данной технологии изучены недостаточно, например, место проведения обжатия и его величина, скорость обжатия заготовки, которые определяются тепловым состоянием слитка: взаимосвязью между глубиной жидкой фазы, шириной двухфазной зоны, распространением фронта и скоростью кристаллизации.
Известные задачи определения динамики затвердевания расплавов при обжатии в основном решены современными средствами математического моделирования на основе численных методов с достаточной для практических целей достоверностью. Для более детального изучения процессов, протекающих в затвердевающем слитке при обжатии, необходимы аналитические решения. Но круг краевых задач теплопроводности в области с подвижной границей, для которых они существуют, довольно ограничен [28].
Указанные выше недостатки сдерживают применение технологии «мягкого» обжатия в практике непрерывной разливки стали на МНЛЗ.
В настоящей диссертации излагаются результаты разработки и совершенствования обобщенной схемы расчета «мягкого» обжатия, предназначенной для нахождения температурных полей непрерывного слитка в
6 ЗВО, ширины двухфазной зоны с целыо определения фильтрации расплава в этой зоне и нахождения величины обжатия при применении данной технологии. Получены численные и аналитические решения задачи распределения температуры по ширине двухфазной области при различных скоростях обжатия слитка.
Данная диссертация состоит из четырех глав. В первой главе приведен обзор литературы, содержащий современные научные представления о предмете исследования: изложены различные модели и методы решения задач затвердевания слитка; рассмотрены влияния на кристаллизующийся слиток внешних воздействий; приведены существующие инженерные методики расчета температуры, твердой корочки. Во второй главе разработана обобщенная схема обжатия слитка с жидкой сердцевиной, приведено описание модели теплового состояния слитка металла и результаты ее реализации. В третьей главе рассмотрена модель теплового состояния двухфазной зоны слитка при «мягком» обжатии, результаты ее применения. Изложены аналитические решения задачи нахождения температуры в данной зоне. Четвертая глава посвящена разработке инженерной методики расчета обжатия слитка, которая позволяет подавлять пористость в его осевой части и учитывать технологию разливки; а также разработке методики расчета фильтрации расплава в двухфазной области.
Настоящая работа содержит 158 страниц печатного текста, включая 42 рисунка, 9 таблиц и список литературы, состоящий из 125 наименований.
Изложенные в диссертации материалы являются результатом обучения автора в заочной аспирантуре Череповецкого государственного университета в период 2001-2005гг. По материалам диссертации опубликовано 7 печатных работ в научных сборниках.
Автор пользуется случаем выразить благодарность к.т.н., доценту Н.В. Телину за научное руководство и помощь в написании диссертации, а также к.ф.-м.н., доценту В.П. Егорову; к.т.н., доценту Д.И. Габелая, сотрудникам кафедр математики и промышленной теплоэнергетики ЧТУ.
Основные виды применяемых математических моделей
Разливка стали и се затвердевание являются важнейшим этапом металлургического производства. Повышение качества металла, уменьшение трудовых, материальных, энергетических затрат - основные направления в деятельности металлургических предприятий. Эти пели реализуются путем внедрения новых технологий [1].
С 50-х годов 20 иска в нашей стране начато промышленное внедрение прогрессивного метода непрерывной разливки стали, который позволяет значительно повысить выход годного и улучшить качество металла, а также облегчает механизацию и автоматизацию процесса разливки.
В настоящее время широкое применение непрерывной разливки стали не только в России, но и в таких промышленно-развитых странах, как США, Япония, Германия и других, обусловлено рядом причин: 1) сокращением цикла металлургического производства, 2) уменьшением капитальных затрат более чем на 30 % за счет отсутствия обжимных станов и отделения нагревательных колодцев, 3) повышением производительности труда, 4) улучшением качества непрерывных слитков и структуры металла, например, повышается степень однородности слитка, 5) увеличением выхода годного продукта, 6) снижением себестоимости слитка, 7) снижением энергопотребления. Наконец, при непрерывной разливке достигается значительное улучшение организации производства, условий труда и окружающей среды [2].
Эти преимущества создают предпосылки для дальнейшего развития способа непрерывной разливки стали, а, следовательно, для совершенствования технологии разливки, модернизации действующих и сооружения новых машин непрерывного литья заготовок (МНЛЗ) различной модификации.
Основными узлами МНЛЗ являются охлаждаемый кристаллизатор, зона вторичного охлаждения (ЗВО), поддерживающая система, тянущее устройство и механизмы для разделения и транспортировки слитков. Различия применяемых и разрабатываемых конструкций МНЛЗ состоят главным образом в расположении слитка в процессе литья. По этому признаку выделяют следующие основные типы МНЛЗ: вертикальные установки с резкой заготовок в вертикальном положении; вертикальные с изгибом заготовки; радиальные установки с постоянным радиусом изгиба заготовки; криволинейные с переменным радиусом изгиба; наклонные установки; горизонтальные установки. Принципиальные схемы непрерывной разливки отличаются положением продольной технологической оси кристаллизующего слитка, однако основы технологии разливки являются общими для всех типов машин.
Принцип работы МНЛЗ рассмотрим па примере криволинейной машины непрерывного литья заготовок ОАО « Северсталь». Машина предназначена для : производства слябов толщиной 200 - 315 мм, шириной 1000 - 1900 мм и длиной 700 - 10500 мм. Система электроприводов механизмов основной технологической линии позволяет вести разливку всего марочного состава стали иа скоростях до 1,6 м/мин. Машина двухручьевая, с независимым оборудованием для каждого ручья, криволинейного типа с радиальным кристаллизатором и плавным выпрямлением слитка с жидкой фазой. Все производственные процессы механизированы и, по возможности, автоматизированы. Предусмотрена возможность ручного управления работой всех механизмов. Схема данной МНЛЗ представлена на рисунке 1.1. Жидкая сталь, имеющая температуру 1540С, из разливочного ковша подастся в промежуточный ковш 1, который предназначен для снижения и стабилизации ферростатического давления и динамического напора струи, отделения шлака и стабилизации температуры перед кристаллизатором. Промежуточный ковш распределяет металл в кристаллизаторы в зависимости от количества ручьев, в рассматриваемой машине их два. Далее сталь попадает в водоохлаждасмый кристаллизатор 2, где происходит начальное формирование непрерывного слитка. За счет интенсивного охлаждения по периметру слитка затвердевают поверхностные слои металла, образуя твердую корочку. Внутри слитка по центральной оси сохраняется жидкая фаза. Для обеспечения стабильности процесса разливки температура металла в кристаллизаторе должна быть на 15-20 С выше температуры затвердевания. Стальная заготовка формируется в соответствии с формой и размерами кристаллизатора. Перед началом разливки в кристаллизатор вводят так называемую затравку, которая является его дном на начальной стадии разливки. Затравка сцепляется с застывшей в кристаллизаторе сталью, а кристаллизатор совершает возвратно-поступательное движение с заданной частотой качания для предотвращения прилипания жидкой стали к стенке.
На выходе из кристаллизатора толщина затвердевшей корочки должна быть не менее 20-30 мм для обеспечения достаточной прочности заготовки, температура на поверхности слитка составляет не более 1100-1200 С при средней температуре корочки 1300-1350С [2]. Образующийся слиток вытягивается вниз с помощью тянущих клетей в зону вторичного охлаждения 3, где происходит его дальнейшее формирование. Слиток движется между роликами 4 поддерживающей системы, предохраняющей оболочку заготовки от деформаций под действием ферростатического давления, и форсунками 5, подающими распыленную воду на поверхность слитка для дальнейшего его охлаждения. В конце зоны вторичного охлаждения температура поверхности слитка снижается до уровня 800-900 С. По окончании полного затвердевания, вытягиваемый с помощью тянущих клетей слиток поступает в газорезку 6, где делится на мерные куски, которые затем отправляются либо в прокатный цех, либо на склад готовой продукции.
Инженерный метод расчета затвердевания слитка
Гидродинамика расплава оказывает существенное влияние на ход теплофизичсских процессов кристаллизации. При непрерывной разливке стали в затвердевающем слитке происходит вынужденное движение в жидкой фазе при воздействии струи металла, поступающего в кристаллизатор из промежуточного ковша через разливочный стакан. Далее энергия этой струи постепенно уменьшается в соответствии с законами ее распространения, после чего решающее значение приобретает естественная конвекция жидкого расплава.
Естественной (свободной или тепловой) называется конвекция, вызванная перегревом расплава относительно температуры затвердевания. В работе [8] В.А.Ефимовым показано, что при увеличении перегрева от 1 К до 40 К в слитке спокойной стали средняя скорость тепловой конвекции возрастает от 0,01 до 0,35 м/с. В непрерывных слитках скорость свободной конвекции имеет участок разгона, а затем затухает по мере сокращения размеров жидкого ядра и снятия перегрева [9]. Естественная конвекция может быть вызвана и градиентами сил поверхностного натяжения на свободной поверхности расплава [10]. Воздействие конвекции на процесс кристаллизации проявляется следующим образом: увеличивается теми переноса тепла на границе затвердевания, благодаря чему возрастает скорость продвижения границы; изменяется структура слитка; изменяется распределение примеси, а также теми переноса неметаллических включений в жидкой фазе слитка [2].
В процессе охлаждения и кристаллизации происходит уменьшение объема металла, так называемая усадка стальных заготовок. Усадка слитка приводит к возникновению стефановских потоков [II], направление которых полностью определяется соотношением плотностей твердой и жидкой фаз. Влияние стефановской конвекции проявляется лишь при малых перегревах и большой усадке. Различие в растворимости примесей в твердой и жидкой фазах приводит к концентрационной неоднородности и появлению термоконцентрационной конвекции [12,13], которая, в отличие от тепловой, не затухает со временем. Интенсивность ее снижается с уменьшением содержания примеси.
Конвективное движение расплава вызывается и внешними воздействиями, которые приводят к вынужденной конвекции жидкой фазы слитка, скорость которой может значительно превышать скорость свободной конвекции [5].
Конвекция расплава имеет сложный характер и оказывает влияние на ход процесса затвердевания. С увеличением перегрева расплава тепловая конвекция становится определяющей, ее качественная картина не изменяется с учетом концентрационной конвекции [14]. На определенной стадии затвердевания в жидкой зоне вследствие растущей вязкости расплава естественная конвекция прекращается, и в нижней части заготовки осевая зона затвердевает в условиях застоя расплава, т.е. по мере прохождения слитка по МНЛЗ влияние конвекции уменьшается [18]: в кристаллизаторе оно велико, а в ЗВО ее можно не учитывать. Теплоперснос в условиях фазового превращения определяет обе стороны процесса перехода металла из жидкого в твердое состояние. Тепловые условия в слитке (в частности, температурное поле слитка) являются главными факторами. Процесс затвердевания непрерывного слитка, связанный с теплоотводом, определяется теплофизическими свойствами металла: теплопроводностью, теплоемкостью и скрытой теплотой кристаллизации (или теплотой фазового превращения). Затвердевание сплавов проходит в интервале температур ликвидуса и солидуса, в нем же в пределах двухфазной зоны выделяется скрытая теплота кристаллизации, численная величина которой зависит от природы сплава и его химического состава. В общем, для большинства сталей, разливаемых непрерывным способом, она может характеризоваться средним значением, равным 272 кДж/ кг. Стремление интенсифицировать процесс непрерывной разливки стали наталкивается на трудности, связанные с ограничением скорости затвердевания, которая зависит от формы и размеров слитка, от ряда технологических и теплотехнических факторов и изменяется в широких пределах [15,16]. На основании опытов некоторыми авторами установлено, что при непрерывной разливке стали в течение 5 с затвердевание идет при максимальном отводе тепла. Плотность теплового потока изменяется от 4,5 до 1,16 мВт/м2, а скорость затвердевания изменяется в пределах от 120-г 200 до 50 мм/мин. В условиях криволинейных МНЛЗ максимальная скорость кристаллизации составляет 1,0 - 1,1 мм/с (или 60 66 мм/мин) [16]. В начальный период разливки средняя скорость затвердевания в кристаллизаторе при увеличении толщины слитка не изменяется. Существенное влияние на нее оказывают соотношения поверхности, объема заготовки и сторон. Для углеродистых сталей на выходе из кристаллизатора скорость затвердевания изменяется в пределах \5 22 мм/ мин. В зоне вторичного охлаждения основную долю в теплоотводе составляет тепло, отводимое от твердой корки слитка [15]. Величины скорости затвердевания для слитков разной толщины изменяются от 1 12 до 12-гІб мм/мин; средняя скорость кристаллизации для круглых слитков составляет 94-10 мм/мин. На основании экспериментальных данных установлено, что скорость кристаллизации возрастает с увеличением расхода воды на вторичное охлаждение. В связи с этим уже при проектировании необходимо определять скорость затвердевания для каждого конкретного случая в зависимости от конструктивных и режимных параметров работы МНЛЗ [6,16].
Скорость затвердевания учитывается и при определении производственной эффективности МНЛЗ [17], также как и величина термических напряжений, которая определяется перепадом температур по сечению (толщине) затвердевшей корочки. Для анализа напряженного состояния слитка необходимо знание закономерностей затвердевания, ведь как показывают опыты, уже в течение первых 5 - 10 с от начала разливки перепад температур по толщине корочки составляет 100 200С, что может привести к возникновению значительных термических напряжений [1] и, как следствие, к появлению трещин [5].
В связи с этим знание процесса затвердевания представляет собой фундаментальную основу для выбора главных технологических факторов, обеспечивающих получение слитков высокого качества: температура жидкой стали, скорость разливки и режим вторичного охлаждения.
Температура жидкой стали - важный фактор, влияющий на процесс и качество непрерывного слитка. При недостаточном перегреве снижается жндкотекучесть стали, затрудняются условия разливки, а значительный перегрев ведет к образованию внутренних трещин н увеличивает осевую усадочную пористость слитка. Поэтому одна из технологических задач -поддержание строгого температурного режима.
Результаты численного решения с учетом конвективных процессов
Исследование процессов теплоотдачи и затвердевания может осуществляться различными методами: экспериментальными, методами математического и физического моделирования.
Экспериментальные методы, связанные с измерением температур в затвердевающем слитке или отливке, разрабатывались большим количеством исследователей. В первую очередь к ним относятся работы Института проблем литья АН УССР под руководством акад. В.А. Ефимова, а также работы Б.Б. Гуляева, О.Н. Магницкого и др. Данные методы исследования применяются в производственных условиях для вычисления положения фронта затвердевания, для изучения температурного поля непрерывного слитка.
Определить границы затвердевающего металла позволяет метод выливания незатвердевшсй части слитка [1]. Граница выливаемости соответствует изотерме внутри интервала кристаллизации и зависит от химического состава стали, скорости затвердевания и др. Толщина корочки рассматривается как средняя величина вследствие неравномерности затвердевания по периметру слитка. При выливании часть жидкого металла удерживается ветвями растущих кристаллов, поэтому данный метод не даст точные результаты.
С целью фиксирования фронта затвердевания применяется метод ввода индикаторов в жидкую часть слитка в конце разливки [25]. В качестве индикаторов применяются радиоактивные изотопы, сера, свинец, вольфрам, которые распределяются в не затвердевшей части слитка. Толщина твердой корочки выводится на авторадиограмме или серном отпечатке. Метод обладает достаточной степенью точности.
Однако указанными методами невозможно точно зафиксировать, например, границу твердой и твердожидкой областей. Экспериментально установлено, что значение корочки соответствует границе выливаемости ( 25-30 % твердой фазы), а толщина затвердевающей корки на выходе из кристаллизатора должна быть, как было сказано выше, не менее 20-30 мм.
Методы фиксации дна жидкой лунки путем заливки жидкого свинца или зондирования дна лунки специальным стержнем используются для определения глубины жидкой фазы, продолжительности затвердевания.
Методы термического анализа, заключающиеся в измерении температур в различных точках сечения слитка, используются для исследования температурного поля непрерывного слитка, а также для нахождения толщины корки и глубины жидкой фазы.
Экс if ери ментальные методы используются для проверки и уточнения решений задач затвердевания, полученных аналитическими или численными методами, однако имеют ограниченную применимость из-за больших расходов металла, повышенной трудоемкости, материальных затрат.
Для исследования гидродинамики разливки стали, изучения циркуляционных и конвективных потоков металла в формирующихся слитках, особенностей затвердевания и других целей широко применяются в настоящее время методы физического моделирования. Они позволяют оценить скорости и направления конвективных потоков в жидком ядре, влияние внешних воздействий на кристаллизующийся слиток, но при этом получается лишь качественная -картина гидродинамических процессов. Физическое моделирование проводится в условиях лаборатории с помощью модельной жидкости, на физических моделях. Данные методы (а также аналоговые) развивались в трудах А.А. Скворцова, А.Д. Акименко, Э.И. Иодко, B.C. Шкляра, В.И. Гребешока, Ю.Н. Яковлева [25].
В последнее время в инженерной практике для изучения температурных полей и процессов теплоотдачи при затвердевании все большее распространение находят методы математического моделирования, к которым относятся аналоговые, аналитические, численные. Математическая модель представляет собой математическое описание физического процесса и предусматривает методы, позволяющие анализировать и исследовать данный процесс.
Метод аналогий находит практическое применение для экспериментального исследования в условиях лабораторий различных тепловых процессов, в том числе теплотехнических вопросов работы МНЛЗ, и заключается в использовании гидротепловой или электротепловой аналогий. Например, метод В.М. Лукьянова, Д.В. Будрина, Б.И. Китаєва, Т.П. Иванцова использует гидр оте иловые аналогии: дифференциальные уравнения распространения тепла теплопроводностью аналогичны дифференциальному уравнению движения жидкости в сообщающихся сосудах [25,17]. Эта аналогия дала возможность создания приборов, с помощью которых, при некоторых допущениях, можно решать задачи, связанные с затвердеванием. Более широкое применение находят методы электрического моделирования, основанные на принципе электротепловой аналогии. Авторы работы [26] устанавливают аналогии температурного поля в процессе затвердевания с нестационарным электрическим полем с подвижной границей.
С помощью аналитических методов решения задач затвердевания устанавливается распределение температур в кристаллизующем слитке в виде непрерывных функций координат и времени, движение границы затвердевания. В настоящее время известен ограниченный круг задач кристаллизации, для которых возможно точное аналитическое решение [27,28].
Одним из немногих примеров точного решения является классическая задача Стефана о промерзании грунта [27]. Однако применительно к затвердеванию стального слитка в этой задаче применяются упрощенные граничные и некоторые другие условия затвердевания. Ценность решения этой задачи состоит в том, что до настоящего времени в практических расчетах используется полученный закон квадратного корпя, связывающий толщину твердой корочки со временем затвердевания. Данный закон хорошо работает только для полуограниченных тел. Применение метода Стефана для плоского слоя встречает большие затруднения.
Модель теплового состояния двухфазной зоны слитка при «мягком» обжатии
Задачи фазового перехода из жидкого состояния в твердое и обратно называются задачами Стефана по имени австрийского математика, изучавшего в 70-89 гг. 19 в. процесс затвердевания талого грунта. В классической постановке плоская задача Стефана формулируется следующим образом [28].
Рассмотрим жидкую массу, ограниченную с одной стороны плоскостью ,Y=0 и неоіраниченно простирающуюся в другую сторону. Пусть в начальный момент времени т = 0 температура в жидкой массе всюду постоянная /о Граничная поверхность длительно поддерживается при некоторой постоянной температуре t\ ниже точки затвердевания жидкой массы /,;. В таком случае прилегающий слой быстро затвердевает, и граница затвердевания будет со временем все дальше и дальше проникать внутрь жидкой массы. Пусть 1{{х,т) и h(x,z) —температуры соответственно твердой и жидкой фаз, а поверхностью их раздела является плоскость х = с (т). Переход из одной фазы в другую сопровождается поглощением или выделением определенного количества теплоты, которое называется теплотой перехода. При затвердевании (кристаллизации) жидкой массы происходит выделение теплоты. При этом теплота кристаллизации равна теплоте плавления.
Таким образом, для определения закона движения поверхности раздела твердой и жидкой фаз и температуры в каждой из них имеется следующая краевая задача: где а\, а2- коэффициенты температуропроводности где L,, — удельная теплота плавления (количество теплоты, которое нужно сообщить единице массы твердого тела, находящегося при температуре плавления, чтобы перевести его в жидкое состояние), р -плотность образующейся фазы; Аь Я2 - коэффициенты теплопроводности. В постановке задачи функция д = f (т) — свободная граница, которая не задана и подлежит определению вместе с функциями f,- (х,т). Таким образом, при классической задаче Стефана отыскивается решение двух дифференциальных уравнений параболического типа для сопряженных областей при заданных краевых условиях и условии сопряжения областей. В результате решения И. Стефана получается функция, связывающая переменную границу раздела фаз и время, представляющая собой так называемый «закон квадратного корня» : с, = к4т ( к- коэффициент затвердевания). В соответствии с этим законом в начальный момент времени скорость перемещения границы раздела фаз равна бесконечности, что противоречит физической природе протекаемых процессов. Задачи Стефана подробно излучались и изучаются как учеными-теоретиками, так и прикладниками. Главная трудность решения задачи Стефана состоит в том, что. определение закона затвердевания и-поля температур в слитке взаимосвязано: скорость перемещения границы раздела фаз зависит от градиентов температуры по обе стороны границы (согласно-условию Стефана), а поле температур, т.е. и градиентов температуры, зависит от толщины отвердевшего слоя расплава. Однакб, как показали исследования, в "определенных условиях поле температур в твердой оболочке слитка стабилизируется, так что закон распределения температуры по сечению твердой корки почти не зависит от условий на межфазной границе [ 18]. Это было учтено Л.С. Лейбензоном, предложившим метод приближенного решения задачи Стефана [50]. Он состоит в использовании интегральных балансовых соотношений при линейном распределении температуры по толщине отвердевшего слоя, т.е. в замене истинного распределения температуры внутри каждой фазы квазистационарным, таким, которое удовлетворяет по пространственным координатам уравнению Лапласа в области с границей, изменяющейся в соответствии с условиями Стефана. Использование стабилизированного распределения температуры в отвердевающем расплаве для упрощенного решения задачи Стефана применил н А.И. Вейник, которому удалось получить несложные расчетные соотношения, связывающие толщину отвердевшего слоя расплава со временем [4,51]. В этих работах приводятся упрощенные решения задачи Стефана для затвердевающих тел не только в форме плиты, но и в форме цилиндра и шара. Аналогичные решения предлагались и другими авторами, обсуждение работ которых приведено в монографии Л.А. Коздобы [52]. Задачи Стефана изучаются в работах Б.Я. Любова [24, 53,54]. Различные методы решения задачи Стефана подробно рассматриваются в книге Л.И. Рубинштейна [55]. Например, М. Бриллюэн пытался найти точное решение задачи путем сведения ее к системе нелинейных интегро-дифференциальных уравнений. Губер разработал обобщенный метод полигональных приближений Коши - Липшица на случай одномерной задачи Стефана. Он заключается в следующем. Интервал времени ( О, Г), где ищется решение, разбивается точками на малые участки; y(t)- скорость продвижения границы раздела фаз Ак, берется постоянной и определяется условием Стефана, записанным для момента t = и температурами обеих фаз. Температура определяется через краевые значения: область существования каждой фазы на А , переводится в отрезок с помощью аффинного преобразования с использованием инвариантности уравнения теплопроводности относительно преобразования Аппсля и представление первой краевой задачи на отрезке с помощью функции Грина. Метод очень громоздкий.
Сам Л.И. Рубинштейн предложил редукцию задачи Стефана к интегральным уравнениям типа Вольтера [55]. Метод основан на прямом использовании тепловых потенциалов. Автор рассматривал решение одномерной задачи Стефана при помощи численного метода. Применял его для решения задачи Стефана для уравнения теплопроводности с непрерывно распределенными источниками тепла, нелинейно зависящими от температуры, се производной по пространственной координате, границы раздела фаз и скорости се продвижения при нелинейных условиях, как на известной, так и на неизвестной границе. Также использовал тепловые потенциалы и метод продолжения решения за іраницу области Колодиер. Метод Лоткина основан па преобразовании области существования каждой фазы в отрезок [55].