Содержание к диссертации
Введение
Глава I. Исследование динамики спинодального распада жидкого раствора . 40
1.1. Экспериментальная методика исследования спинодального распада при глубоком заходе в лабильную область. 42
1.2. Эксперимент по наблюдению спинодального распада в ассоциированном водном растворе . 45
1.3. Описание динамики спинодального распада в приближении эффективной свободной энергии. 54
Глава II. Оптический метод определения бинодали и спинодали ассоциированного раствора . 64
2.1. Локальное светоиндуцированное расслоение. 64
2.2. Экспериментальная реализация оптического метода определения бинодали и спинодали 72
Глава III. Исследование нелинейного режима распространения импульса в гетерофазных мелкодисперсных поглощающих жидкостях . 86
3.1. Нелинейные режимы распространения мощного лазерного
импульса в однокомпонентной жидкости и в расслаивающемся растворе. 87
3.2. Экспериментальное исследование светоиндуцированного самопросветления в однокомпонентной жидкости и бинарной жидкой смеси; приложения для пассивной модуляции добротности лазеров . 90
3.3. Теоретический анализ эффекта нелинейной экстинкции при распространении лазерного импульса в гетерогенной поглощающей жидкости. 101
Глава IV. Бабстонная структура как самостоятельная фаза молекулярной жидкости 115
4.1. Проблема стабильности газовых пузырьков в жидкости. 117
4.2. Взаимодействие иона с пузырьком В ЖИДКОСТИ. 128
4.3. Скорость адсорбции и десорбции ионов на поверхности пузырька. 151
4.4. Параметры бабстонов и условия их существования . 156
4.5. взаимодействие бабстонов. 170
4.6. спонтанное образование бабстонных зародышей. 174
4.7. Образование бабстонов и бабстонных кластеров. 184
Глава V. экспериментальные исследования бабстонно-кластерной структура однородной прозрачной жидкости . 207
5.1. Применение методов малоуглового рассеяния для исследования бабстонов и бабстонных кластеров. 207
5.2. индикатриса рассеяния света на бабстонных кластерах. 218
5.3. экспериментальное определение параметров бабстонного
кластера с помощью малоуглового рассеяния света. 226
5.4. Внутренняя структура отгазованной воды; эксперимент по четырехфотонной поляризационной спектроскопии комбинационного рассеяния. 243
Глава VI. Применение модели бабстонных кластеров для объяснения механизма оптического пробоя однородных прозрачных жидкостей и гидрофобного взаимодействия . 271
6.1. Развитие электронной лавины внутри бабстонов. 275
6.2. Коалесценция бабстонных кластеров. 286
6.3. Ионизация и нагрев тяжелых частиц; испарение жидкой стенки пузыря. 292 6.4. Физические явления, сопутствующие оптическому пробою жидкостей. 296
6.5. оптическая кавитация. 306
6.6. Зависимость экспериментального порога от плотности кластеров и параметров фокусировки; определение плотности кластеров в жидкости. 310
6.7. Множетвеншй характер оптического пробоя в жидкости. 318
6.8. Зависимость пороговой интенсивности от температуры. 321
6.9. Механизм оптической кавитации в поле широкополосной лазерной накачки. 325
6.10. Исследование оптической кавитации в расслаивающейся жидкой смеси. 344
6.11. Применение модели бабетонных кластеров для объяснения механизма гидрофобного взаимодействия в коллоидных системах. 352
Заключение 362
Литература
- Эксперимент по наблюдению спинодального распада в ассоциированном водном растворе
- Экспериментальная реализация оптического метода определения бинодали и спинодали
- Экспериментальное исследование светоиндуцированного самопросветления в однокомпонентной жидкости и бинарной жидкой смеси; приложения для пассивной модуляции добротности лазеров
- Параметры бабстонов и условия их существования
Введение к работе
Применение лазерных методов в исследованиях фазовых
СОСТОЯНИЙ 5КИДК0СТЄЙ ПОЗВОЛИЛО Качественно ПОВЫСИТЬ vnOBCHb этих
исследований. Важную роль играет использование интенсивного лазерного излучения при воздействии на среду. При этом появляется возможность наблюдать вызванные таким воздействием нелинейные эффекты в среде. Нас будет интересовать возможность инициировать фазовые переходы (ФП) в жидкостях при лазерном воздействии, такие как расслоение жидкого бинарного раствора и оптический пробой (плазмообразование) прозрачной для излучения жидкости, насыщенной растворенным газом и содержащей ионную примесь. При этом мы не рассматриваем ФП, вызванные поглощением излучения (типа вскипания).
Актуальность темы. Жидкий бинарный раствор может находиться в одном из трех фазовых состояний: стабильном, метастабильном и лабильном (абсолютно неустойчивом) состоянии. Линия на фазовой диаграмме (в координатах температура -концентрация), разделяющая области стабильных и метастабильных состояний, называется бинодалью, а граница между метастабильным и лабильным состояниями называется спинодалью. Лабильное состояние до сих пор недостаточно исследовано в экспериментах, что обусловлено малым временем жизни раствора в этом состоянии. Процессы в расслаивающихся растворах, находящихся в метастабильном и лабильном состоянии, моделируют многие явления в биологических системах, происходящие в неравновесных условиях, поэтому изучение их кинетики представляет несомненный интерес. Универсальность ФП различной природы позволяет надеяться, что их свойства, характеріше для расслаивающихся растворов, проявлются и
в других фазовых системах, в частности, в гетерогенных смесях "жидкость - пузырьки газа", что важно для понимания процессов жизнедеятельности.
Целью настоящей работы является исследование с помощью лазерного излучения фазовых состояний жидкостей, а также светоиндуцированных фазовых переходов в системах "жидкость -жидкость" и "жидкость - растворенный газ".
Новизна работы заключается:
1) в применении тонкослойных кювет для наблюдения
спинодального распада при глубоких заходах в лабильную область, а
также эффектов, связанных с изменением концентрации раствора в
метастабильной и лабильной областях при нетешговом воздействии
лазерного излучения. Показано, что в таких кюветах подавлено
конвективное необратимое разделение расслаивающегося раствора на
два несмешивающихся слоя. Поэтому появляется возможность
добиться глубокого захода в лабильную область при изменении
температуры с помощью термостата. При этом также удается
увеличить время наблюдения системы в метастабильном и лабильном
состояниях.
-
в наблюдении автоколебательного режима спинодального распада при глубоком заходе в лабильную область. Это указывает, что модуляционная неустойчивость, характерная для нелинейных волновых систем с межмодовым взаимодействием, может возникать и в нелинейных системах диффузионного типа.
-
в наблюдении слабого бародиффузионного эффекта в жидкости, благодаря которому удается перевести раствор из стабильной в метастабильную область и определить положение бинодали расслаивающегося раствора в широком диапазоне температур и концентраций.
4) в предложении модели мезоскопической (с характерными
масштабами в диапазоне 1 - 100 нм) структуры молекулярной
жидкости, насыщенной растворенным газом и содержащей ионную
компоненту. Показано, что в такой жидкости вдали от точки кипения
спонтанно возникают газовые микропузыри, которые могут
стабилизироваться за счет адсорбции на их поверхности ионов одного
знака. Количественно решена задача об установлении адсорбционно-
десорбционного равновесия таких микропузырей с растворенными в
жидкости ионами, что позволило определить равновесные
характеристики микропузырей (их размер, заряд, объемную
плотность) в зависимости от параметров жидкости (плотность ионов,
газосодержание и диэлектрическая проницаемость), температуры и
давления.
5) в обнаружении влияния растворенного газа на
низкочастотный спектр воды, что было получено методом
четырехфотонной поляризационной спектроскопии для отгазованной
и неоттазованной воды.
6) в предложении нового механизма оптического пробоя
прозрачной для лазерного излучения жидкости, в котором затравками
пробоя являются кластеры из микропузырей растворешюго газа.
Предложенный механизм позволяет объяснить ряд особенностей
оптического пробоя в жидкости, которые отличают этот процесс от
пробоя в газах.
Практическая ценность работы определяется возможностью использовать результаты исследования фазовых состояний расслаивающихся растворов для моделирования многих биологических процессов. Реализация светоиндуцированного изменения концентрации за счет нетеплового лазерного воздействия может быть использована в технологических процессах с применением
лазерного излучения. Предложенный механизм оптического пробоя дает основу для изучения (в том числе и дистанционного) определенных свойств жидкого состояния.
Анробадиа работы и публикации. Основные научные результаты диссертации опубликованы в 36 журнальных статьях и докладывались на II Европейской Конференции по Квантовой Электронике (Дрезден, 1989), на XIV Международной Конференции по Когерентной и Нелинейной Оптике (Ленинград, 1991), на II и III Конференциях по Жидкому Состоянию (Флоренция, 1993; Норвич, 1996), на X Международном Симпозиуме по Поверхностно-Активным Веществам в Растворах (Каракас, 1994), на 48 Ежегодном Заседании по Коллоидной Химии (Саппоро, 1995), на IX Международной Конференции по Поверхности и Коллоидным Системам (София, 1997), а также на семинарах в ИОФ РАН, ИФХ РАН, Европейской Лаборатории по Нелинейной Спектроскопии (Флоренция), Институте Атомной и Молекулярной Физики (Пиза), Факультете Энергетики и Прикладной Физики Университета г.Палермо, Механическом Факультете Калифорнийского Университета (Беркли), Отделения Прикладной Математики Австралийского Национального Университета (Канберра), Химического Факультета Университета г.Мельбурн.
Представленные в диссертации исследования проведены при поддержке проектов Российского Фонда Фундаментальных Исследований № 94-02-05823 и № 96-02-17236, а также международных проектов:
Grant from Japan Society for the Promotion of Science (JSPS), Program for Collaboration of Russian and Japanese Scientists, 1995-1996;
International Science Foundation, Grant No N75000,1994-1995;
International Science Foundation and Russian Government, Grant No N75300, 1995.
Объем работы. Диссертация содержит 379 страниц текста, включая 62 рисунка, 5 таблиц и библиографию из 258 наименований.
Основные положенно, представляемые к защите.
1. В двухкомпонентном жидком расслаивающемся растворе при
глубоком погружении в лабильную область реализуется
автоколебательный режим спинодального распада.
2. Оптотермодинамический метод воздействия на бинарные
жидкие смеси позволяет экспериментально определить положение
бинодали и спинодали в координатах температура - концентрация
для расслаивающихся растворов с нижней критической точкой.
3. Важным механизмом лазерного воздействия на
слабопоглощающие бинарные расслаивающиеся растворы при
интенсивностях ниже порога пробоя является светоиндуцированная
бародиффузия.
4. В жидкости, находящейся в равновесии с растворенным газом
и содержащей ионную компоненту, спонтанно образуются
микропузыри растворенного газа, которые могут стабилизироваться
за счет адсорбции ионов на их поверхность.
5. Возникающие в равновесной системе "жидкость +
растворенный газ + ионная примесь" стабильные микропузыри в
результате коагуляции формируют кластеры, обладающие
фрактальными свойствами.
6. Затравками для оптического пробоя в прозрачных жидкостях
служат стабилизированные ионами микропузыри.
7. Оптический пробой прозрачной жидкости обусловлен
развитием электронной лавины внутри микропузыря.
Эксперимент по наблюдению спинодального распада в ассоциированном водном растворе
Теория СР, основанная на линеаризованном уравнении диффузии, трименима, как уже сказано, лишь к начальным стадиям распада, когда рлуктуации концентрации малы. На более поздней стадии предположение о лалости величины и - и становится неправомерным из-за постоянного ее роста. На этой стадии временная динамика интенсивности рассеяния соответствует степенному закону [17 - 22,, I(tt t", причем гоказатель степени [3 может зависеть и от времени, и от глубины вторжения в лабильную область (в [171 специально выделен режим с неизменным во времени показателем (3). Аналогичный описанному в [16] экспериментальный метод применен для что на определенных стадиях распада справедлива аппроксимация I(t) ос t1/3 для всех исследованных значений глубины захода в лабильную область. В [25] зучена также кинетика СР в зависимости от глубины захода; получено, ЇТО при А27 2-Ю" К зависимости q (t) и I1( ((t) хоррош согласуются с теорией Кавасаки, описывающей степенной закон по t [20]. При AT 2-10 К согласие теории и эксперимента исследования СР в растворе "2-6-лутидин + вода" с НКТ [23, 24]. Было показано, исчезает, что может быть связано с конечной скоростью изменения температуры в эксперименте.
На развитой стадии СР происходит дальнейший рост рассеивающих структур (капель одной из фаз, диспергированных в другой фазе); зависимость Iitt определяется трансцендентным уравнением Фурукавы [2D. Интересная особенность динамики СР обнаружена в [17]] На начальной стадии масштаб капель характеризуется единственной зависящей от t величиной - размером капли сопряженной фазы Я. Однако, когда концентрация в центральных областях капель равновесна, а на их границах еще далека от равновесия, появляется еще один зависящий от t тространственный масштаб - толщина межфазного слоя 3. Наконец, на завершающей стадии распада перепад концентрации в межфазном слое настолько резок, что й перестает зависеть от t - имеет место возврат к ситуации, когда только один пространственный масштаб зависит от и R(t). (Ниже будет показано, что временная "возвращаемость" при СР -это одно из фундаментальных свойств этого явления). Мз приведенного здесь краткого (и далеко неполного) обзора работ по динамике СР следует, что полной ясности в этом вопросе до сих пор нет.
Перевод расслаивающегося раствора в лабильное состояние возможен гакже при тепловом воздействии излучения. Так, в экспериментах [32, 33] он осуществлен в водном растворе "триэтиламин + бутилцеллозольв" с ЖТ за счет разогрева в результате объемного энерговыделения при юглощении мощного излучения. Для исследования отдельных стадий СР использовано излучение моноимпульсного УАОгШ3 -лазера. Различные режимы СР при конечной скорости захода в лабильную область реализованы использованием серии импульсов свободной генерации YAG:M3+ a3epa, а гакже широкополосного излучения импульсной ксеноновой лампы. 1рименение этого метода для перевода раствора в лабильное состояние тозволило существенно увеличить глубину и скорость захода в лабильную область, что значительно ускорило релаксационные диффузионные 1роцессы. При этом было показано, что в поглощающих расслаивающихся растворах при воздействии на них мощного излучения возникают зветонаведенные концентрационные структуры. Это обеспечивает присущий кидким смесям механизм светоиндуцированного диффузионного терераспределения компонентов и усиление этого эффекта при заходе в лабильную область. Светоиндуцированные концентрационные структуры при определенных условиях играют роль затравок для СР. В [34] определен жлад в процесс фазового разделения как спонтанной самодиффузии, так и зветоиндуцированных диффузионных механизмов, связанных с терме- и Оародиффузией, температуропроводностью и светоиндуцированным изменением Лх. Ранняя и поздняя стадии СР изучены в [34] не только по динамике "спинодальнего кольца" в картине рассеяния, но и по изменению коэффициента экстинкции зондирующего излучения. На ранней стадии коэффициент экстинкции растет линейно со временем (ос гt), где 1/Г соответствует времени появления модулированной пространственной структуры; Г зависит от скорости подвода тепла q dQ/ut как Г д , где ф = 0.65.
Интересная методика при переводе расслаивающегося раствора в лабильную область предложена в [35]] Смесь "метанол + гептан" с верхней критической точкой при уменьшении температуры переводилась из докритической области в закритическую. При выходе на бинодаль должно начаться расслоение, обусловленное конвекционным разделением тяжелой и легкой компонент. Расслоение подавляется за счет интенсивного перемешивания жидкости, и таким способом удавалось достаточно долго поддерживать закритическое состояние. Отметим наконец, что лабильное состояние "сохраняется" в растворах полимеров дольше, чем в обычных жидкостях. Скорость расплывания упорядоченной структуры СР за счет конвективного противотока легкой и тяжелой фаз мала в таких растворах из-за большой вязкости [27 - 30], а также если плотности образовавшихся при фазовом разделении фракций близки [17, 31]. Исследованию динамики СР при глубоком заходе в лабильную область посвящена первая глава первой части диссертации.
Во второй главе первой части диссертации рассмотрены различные режимы перевода системы в закритическую область, причем в этих экспериментах удалось определить положение и бинодали, и спинодали расслаивающихя растворов.
Экспериментальная реализация оптического метода определения бинодали и спинодали
Ткким .бразом, широко принятая точка зрения о том, что оптический про о мидкоете ишициируется поглощающимз микровключениями, пт нашему мнению, может иыть иправедлива лишь ирикенительно к споциально пригиюовленным нечистым жидкостям . для которых концентрация включений п 1/V. причем, как отмечено в [75], чрезмерное засорение жидкостей поглощающими микровключениями (в [75] - это продукты пиролиза органических соединений) приводит к сильному нелинейному рассеянию лазерного излучения, связанному с тепловой дефокусировкой и возникновением на частицах паровых пузырьков [76, 77], что препятствует возникновению оптического пробоя. Повышение порога пробоя также наблюдали и мы в упоминавшихся выше экспериментах с бензолом.
Наряду с рассмотренным выше механизмом оптического пробоя в жидкостях в работе [70] отмечалось, что порог пробоя в бензоле и четыреххлористом углероде зависит от концентрации растворенного воздуха, и был сделан вывод, что растворенный в жидкости газ влияет на ее оптический пробой. Однако, дальнейшего развития эти экспериментальные результаты не получили, и концепция поглощающих включений до сих пор является общепринятой [66].
Альтернативной моделью оптического пробоя прозрачных жидкостей является модель электронной лавины в жидкости (см., например, [78 -80]). в рамках этой модели считается, что оптический пробой жидкости имеет ту же природу, что и электрический пробой полупроводника, т.е. принимается, что в жидкости существуют электроны с выской подвижностью [81]. В этой модели основной вклад в пробой вносят так называемые, "счастливые электроны". Направление движения этих электронов изменяется в результате столкновения с атомами, но между двумя последующими столкновениями это направление совпадает с вектором напряженности электрического поля электромагнитной волны, обусловливающей пробой, т.е. эти электроны очень эффективно разогреваются. Однако, такой подход представляется достаточно искусственным хотя бы потому, что в его рамках трудно объяснить множественный характер пробоя. Правда, в работе [82] множественный характер пробоя жидкости при развитии в ней электронной лавины объясняется "горячими точками" в распределении интенсивности излучения в каустике, обусловленными неидеальностью фокусирующей системы. Однако, здесь возникает противоречие с тем, что пробой специально не засоренного поглощающими частицами газа всегда характеризуется однородной плазмой вне зависимости от условий фокусировки. Из приведенного здесь краткого (и далеко неполного) обзора работ по оптическому пробою жидкости ясно, что существует проблема, связанная с инициацией оптического пробоя, т.е. с наличием в жидкости затравок для пробоя. Такими затравками на наш взгляд являются кластеры из газовых микропузырьков. При этом удается объяснить различные эффекты ваблюдаемые при оптическом пробое прозрачных жидкостей. Поэтому зредложенная в шестой главе модель пробоя как формирование плазмы внутри микропузырьков кажется нам более предпочтительной чем описанные выше альтернативные модели. На наш взгляд, микропузыри, распределенные в жидкости между гидрофобными поверхностями, могут обеспечивать взаимодействие между такими поверхностями на достаточно больших растояниях. Остановимся подробнее на этом вопросе.
Дальнодействующее притяжения между гидрофобными поверхностями в жидкости (радиус которого в 10 - 100 раз больше, чем у Ван дер Ваальсова взаимодействия) не может считаться полностью изученным, что к настоящему моменту признается большинством исследователей [127 -1291. Все попытки дать теоретическое объяснение этому эффекту на микроскопическом уровне (флуктуации давления внутри жидкой пленки, переводящие последнюю в метастабильное состояние [130], "воспроизведение" структуры поверхности в приповерхностном слое сольвента [131], флуктуации ионных сил, связанные с ионной адсорбцией [132], адсорбированная газовая пленка [133] или гигантские флуктуации дипольного момента в растворе электролита [134]) не были полностью успешными. В некоторых теориях предсказывалось, что в растворе электролита гидрофобная сила « I/2D, где D - Дебаевский радиус; такая зависимость наблюдалась в [156]. Однако, в общем случае это неверно [157]. Выяснилось, что гидрофобные силы зависят от природы поверхности [127, 135, 136], адсорбции ионов [137], концентрации электролита и его типа [138], концентрации поверхностно - активных веществ (ПАВ) на поверхности (при этом поверхность может быть твердой [129], жидкой или газообразной (пузыри) [139]). Важную роль играет адсорбция растворенного газа между поверхностями [140], а также взаимовлияние между приповерхностной концентрацией электролита и растворимостью газа. Таким образом, не существует единого подхода к проблеме гидрофобных взаимодействий, и эта тема активно обсуждается среди специалистов по коллоидной химии, с гидрофобными взаимодействиями также связан эффект проскальзывания капли воды по поверхности, обладающей гидрофобными свойствами [141, 142] (этот эффект зависит от концентрации растворенного газа [143] и от изменения вязкости сольвента вблизи гидрофобной стенки [144]). Следует также упомянуть эксперименты [160, 161], в ккотрых ззафикирровано ччт ддл отгазованной и обычной воды стабилизация эмульсий и гидрофобных суспензий, фильтрация мельчайших гидрофобных частиц и взаимодействие ионов в мицеллах происходят по разному; это также указывает на роль растворенного газа.
Экспериментальное исследование светоиндуцированного самопросветления в однокомпонентной жидкости и бинарной жидкой смеси; приложения для пассивной модуляции добротности лазеров
Кроме того, эффект не наблюдался для расслаивающихся растворов с одинаковыми молекулярными массами (как и должно быть в случае бародиффузии). Это подтвердилось в экспериментах по "обстрелу" тяжелой и легкой фракций растворов "метилциклогексан (молекулярная масса м = 98 а.е.) + фурфурол (М = 96 а.е.)", а также "изоамиловый спирт (М = 88 а.е.) + глицерин (М = 92 а.е.)". Таким образом, отклик тяжелой фракции раствора "ТМП + вода", находящегося в стабильной области вблизи бинодали, на лазерное воздействие, действительно обусловлен светоиндуцированной бэродиффузией. Насколько нам известно, это первое экспериментальное наблюдение светоиндуцированной бародиффузии в жидкости.
Естественной количественной характеристикой отклика на лазерное воздействие (рис. 2.3 б) служит площадь туманности 5. Мз-за нерегулярной формы самой туманности, а также размытости ее границ, относительная погрешность измерения S в единичном лазерном импульсе KS/S достаточно велика. Повышает точность набор статистических данных за счет облучения кюветы, поддерживаемой при определенной температуре, серией из 250 лазерных импульсов. Каждый последующий импульс попадал в новый участок кювет - в паузах с джттельностью ю с кювета смещалась с помощью двухкоординатного стожка в плоскости поперек пучка на I - 2 мм. В результате усреднения площадей S по набору из 250 независимых значений погрешность измерений площади понизилась до 5 %.
По окончании серии из 250 импульсов и полной релаксации всех "туманностей" температура Т кюветы повышалась и процедура измерения S(T) повторялась. Таким образом, для каждой исходной концентрации раствора и определялись зависимости площади туманности от температуры: s = S(T). Семейство из пяти таких зависимостей показано на рис.2.4 (а - д). Во всех пяти случаях первая серия лазерных выстрелов начиналась после охлаждения кюветы до температуры т Tt(ur) (когда капли легкой фракции отсутствуют); температурный шаг измерений составлял 0.5 К. Как видно из рис.2.4, начиная с некоторых температур величина S(T) возрастает, выходя на плато при температуре !Р1 = Тъ(иг); при этом, как уже отмечалось, само возрастание S(T) начинается при температуре ниже Тъ примерно на I К. Измеряя температуру 2 выхода S(T) на плато мы имели возможность в независимо определить температуру бинодали т . Далее S(T) не имеет особенностей вплоть до температуры Т , при которой испытывает скачок; после этого функция S(T) вновь выходит на плато. Поскольку, как следует из приведенных графиков, при и - и температуры Т - Т - Т , Т естественно связать с температурой спинодали Г (и ). Таким образом, поведение S(T) подтверждает вывод теории 2.. о существовании особенностей зависимости а (Т) в точках бинодали и спинодааж. Отметим что при при температурах ТУТ в растворе спорадически наблюдалась светоиндунігоованная кавитация: в области лазерного ттятна возникал кавитацйонный пузырь (см. рис. 2.5).
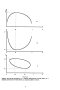
Полученные в эксперименте точки тли ) и Т {и ) представлены на over рис. 2.6. Сплошная линия соответствует бинодали раствора "ТМП + вода", взятой из справочника [61] (см. также рис. 1.1). Видно, что экспериментальные значения тли ) с хорошей точностью ложатся на этт линию, т.е. точки Т (и ) действительно принадлежат бинодали.
Механизм отклика раствора на лазерное воздействие при достижении з г Y конвективный противоток в кювете подавлен и сопряженная фаза диспергирована внутри основной фазы в форме мельчайших капель (см. рис. 2.3 а), т. е. распределение концентрации неоднородно. Выберем в расслоившемся таким образом растворе некоторую область внутри лазерного пятна, причем эта область должна включать досточно много капель сопряженной фазы. Концентрация какого-либо сорта молекул (для определенности, молекул тш в среднем по этой области выражается как uт = if_/(ff. + JL)» где ffm и WВ - количество молекул ТМП и воды в этой области соответственно. Заметим, что йт не есть реальная концентрация смеси в выбранной области, поскольку в каждой точке этой области концентрация определяется абсциссами бинодали и соответствует легкой или тяжелой фракции. Ясно, однако, что й м и , где и - начальная концентрация молекул ТМП, определяемая температурой т., при которой была получена данная тяжелая фракция, см. рис. 2.1. Предположим, что температура т. задаваемая термостатом, такова, что точка (Up. Т) лежит на сшнодали, т.е. Т = т.. Для того, чтобы реализовать лабильное состояние, мы должны перемешать расслоившийся раствор, поддерживаемый при температуре г.. В результате распределение концентрации по выделенной области становится квазиоднородным, т.е.
Параметры бабстонов и условия их существования
Бабстонная структура как самостоятельная фаза молекулярной жидкости. о возможности существования в молекулярной жидкости стабильной структуры из газовых микропузырей было впервые заявлено в работе [881. Согласно развитым в ней представлениям, наличие в жидкости наряду с растворенным нейтральным газом и ионной компоненты, способной адсорбироваться на границе жидкости, приводит к тому, что в ней при определенных условиях могут спонтанно (т.е. в результате тепловых флуктуации) образовываться стабильные газовые пузырьки, названные бабстонами (аббревиатура фразы bubble stabilized by ions). Существенно подчеркнуть, что оба названные необходимыие условия -наличие растворенного газа и ионной компоненты, отвечает скорее обычным, чем исключительным состояниям реальных молекулярных жидкостей, находящихся в контакте с газовой атмосферой (например, воздухом) и всегда обладающих той или иной степенью ионной электропроводности. Даже абсолютно чистая (беспримесная) молекулярная жидкость обладает собственной ионной проводимостью, которая обусловлена электролитической диссоциацией своих молекул, сильно зависящей от температуры. Произвольные молекулярные примеси, содержащиеся в жидкостях, в общем случае следует рссматривать как электролиты (сильные или слабые), обусловливающие примесную проводимость. Можно сказать, что любая молекулярная жидкость, строго говоря, представляет собой ионный раствор.
Таким образом, согласно представлениям работы [881, молекулярная жидкость, вообще говоря, не есть сплошная среда в макроскопическом понимании этого слова - в ней существует структура газовых полостей с размерами, значительно превосходящими межмолекулярные расстояния. Дисперсная среда "сплошная жидкость + бабстоны" неустойчива к коагуляции, т.е. к образованию агрегатов, названных бабстонными кластерами [88]] Гипотеза о существовании в жидкости подобных стабильных агрегатов была впервые высказана в работе [46].
Результаты [46, 883 получили дальнейшее развитие в работах [84 -86, 89, 106, 107, 174, 175]. В [84 - 86] изложены новые физические представления об оптическом (лазерном) пробое прозрачных жидкостей, основанные на гипотезе о существовании в них бабстонно-кластерной структуры. Работы [89, 107, 175] посвящены наблюдению особенностей малоуглового светового и нейтронного рассеяния в чистых жидкостях, обусловленного наличием бабстонно-кластерной структуры. Результаты этих наблюдений свидетельствуют о фрактальном характере такой структуры. В работе [106] представления о бабстонах используются для объяснения механизма дальнодействия при т.н. гидрофобных взаимодействиях. В [174] впервые экспериментально обнаружены новые спектральные линии светорассеяния воды в крыле линии Рэлея; для интерпретации этих линий также использована модель бабстонов.
В этой главе будут даны теоретические обоснования существования бабстонной структуры в молекулярных жидкостях. Это потребует рассмотрения некоторых смежных, но представляющих и самостоятельный интерес вопросов, таких как: селективная адсорбция ионов на поверхности жидкость-газ, образование диффузных ионных оболочек вокруг электрически заряженных газовых пузырей (постановка и решение Дебай - Хюккелевской задачи применительно к бабстонам), кинетика коагуляции бабстонов и образование бабстонных кластеров. В заключение мы обсуждаем возможную роль бабстонной структуры в целом ряде известных физических явлений, наблюдаемых в жидкостях.
Существует целый ряд явлений, относящихся к физике жидкостей, интерпретация которых основана на предположении о существовании в объеме самой жидкости газовых полостей (пузырьков). Необходимость существования таких полостей при этом не исключает и абсолютно чистых жидкостей, лишенных каких-либо взвешенных примесей макроскопических частиц (последние могут содержать поры, заполненные газом [1761). Важно, что такие полости должны (согласно общепринятым представлениям) существовать в стационарных условиях, т.е. быть стабильными. Наиболее ярким примером физического явления, ставшим классическим по однозначности своей интерпретации (основанной именно на предположении о существовании стабильных газовых пузырьков) - это явление акустической кавитации (о других примерах говорится ниже). Без привлечения гипотезы о существовании стабильных пузырьков невозможно объяснить экспериментально наблюдаемые пороги кавитации, которые на несколько порядков (по значениям отрицательного давления) ниже, чем это соответствует молекулярной прочности жидкости р сш „ 10 атм (и _ плотность числа частиц жидкости а -коэффициент поверхностного натяжения).
Вопрос о возможности существования в жидкости стабильных газовых пузырей стоит в физике очень давно, но до сих пор не нашел исчерпывающего ответа. Именно эту ситуацию отражает название настоящего параграфа. Ниже дается количественная формулировка этой проблемы.