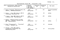Содержание к диссертации
стр.
Введение 3
I глава. Постановка задачи о движении контейнера 9
на участке торможения
I.I.Особенности эксплуатации пневмотранспортных 9
систем и тормозные устройства
1.2 .Фрикционный участок торможения кривом- 17
Н8ЙН0Й форМЫ
1.3.Движение точечного контейнера по 23
тормозному участку
П глава. Выбор формы тормозного участка 29
2.1.Постановка вариационной задачи 29
2.2.Описание метода приближенного решения 37
задачи выбора оптимальной пространственной
кривой
2.3.Решение задачи оптимизации при переменном 47
кручении кривой
2Л.Решение задачи оптимизации при переменных 62
кривизне и кручении кривой
Ш глава. Изучение процесса торможения с учетом 71
конечных размеров контейнера
3.1.Геометрия и кинематика движения контейнера.. 71
3.2.Вывод уравнений движения контейнера по 84-
тормозному участку
3.3. Анализ процесса торможения на участках 101
выбранной формы
3 а к л юч е н и е 117
Ли т е ра ту ра 120
Введение к работе
В настоящее время как в нашей стране, так и за рубежом большое внимание уделяется разработке систем трубопроводного контейнерного пневмотранспорта (ТПК), /2-б/ , /48-50/ Системы ТПК предназначены для транспортирования по трубопроводам в специальных контейнерах различных промышленных грузов. Контейнеры оборудованы колесным опорно-ходовым аппаратом и перемещаются по трубопроводу под действием давления воздуха, который подается в начало трубопровода нагнетательными станциями. Технические характеристики действующих пневмотранспортных систем приведены в табл. І.І. Во многих случаях системы ТПК имеют преимущества перед традиционными видами транспорта. Их применение позволяет эффективно решать задачи транспортирования на расстояние от нескольких сот метров до десятков километров угля, руды, строительных материалов, бытовых отходов городов, почты, книг и других грузов.
Для систем ТПК характерна: простота конструкций, небольшая численность обслуживающего персонала, большая степень автоматизации, независимость эксплуатации от природно климатических условий, возможность использования в стесненных производственных условиях и густонаселенных жилых районах, возможность транспортирования грузов, отравляющих атмосферу или требующих защиты от влияния внешней среды.
Важным элементом пневмотранспортной системы, работа которого во многом определяет пропускную способность ТПК, является участок торможения контейнеров. Исследованию тормозных устройств систем ТПК посвящено большое количество работ [fy] , [9-10/ , /18/ , /21/ , /45; . Анализ работы существующих
Таблица I.I.
Характеристики систем ТПК, построенных в СССР істо строительства, марка системы, предприятие-разработчик
Диаметр трубопровода (мм), тип системы
Дальность (км)
Грузопоток т/час
Вид груза
Карьер Сычевского ГОКа,Московская обл. (ТПК-3), ВНЙЙПИтранспрогресс
Карьер - завод ЖБК (Лило-І, КПТ-І) г.шулавери, Грузинская ССР
К арьер - завод ЖБК (Лило-2, КПТ-2) г.Тбилиси, СКВ "Транспрогресс"
4. Ка _рьер - асфальто-бетонн ый завод КПТ-28) г.Берники, Тульская обл. КБ "Транспрогресс"
5. Шахта "Объединенная" - "Торезская" г.Торез, Донецкая обл. б. Речпорт - завод ЖБК (ТПК-І) г.Дзержинск, Горьковская обл. ВНЙЙПИтранспрогресс тормозных устройств показывает, что в ряде случаев они не удовлетворяют требованиям, предъявляемым к устройствам торможения пневмотранспортной системы и в известной степени сдерживают возможности по увеличению пропускной способности систем ТПК, и, следовательно? их эффективности и конкурентноспособности с другими видами транспорта. Аналогичные выводы сделаны в работе [э] , где приведена классификация тормозных устройств для систем ТПК, для большинства типов тормозных устройств проанализированы схемные решения.
В связи с этим актуальна задача создания новых типов тормозных устройств, которые можно было бы применять в системах с интенсивным движением транспортных единиц. В этом направлении перспективным является устройство торможения, в котором тормозное усилие создается с использованием центробежных сил и сил трения [ill . Исследованию процесса торможения в устройствах подобного типа посвящены работы [цв , 4-7J . В [ц-б] рассмотрен участок торможения, который имеет форму окружности, расположенную на наклонной плоскости. Найдены угол наклона плоскости и точка входа на участок, минимизирующие разброс скоростей движения контейнеров. В работе [ц-7] определены оптимальные параметры тормозного участка, принимающего форму пространственной кривой с фиксированной кривизной. В настоящей работе рассмотрен тормозной участок, который может принимать форму любой пространственной кривой с непрерывно изменяющейся касательной.
Целью работы является построение математической модели движения контейнера на криволинейном участке торможения и на ее основе изучение особенностей процесса торможения - б - для таких устройств, а также создание методики расчета основных параметров тормозного участка. Выбор параметров предполагает решение некоторой экстремальной задачи, то есть отыскание наилучшего решения в соответствии с определенными критериями. В работе решается задача выбора пространственной конфигурации тормозного участка, при которой разброс скорости в конце торможения минимален.
В этой задаче часть параметров влияющих на процесс торможения неизвестна, для них заданы лишь допустимые области изменения. По этой причине поставленная экстремальная задача есть задача управления ансамблем траекторий, полученных объединением решений по всем неизвестным параметрам. Теория управления в условиях неопределенности получила развитие в трудах Н.Н.Красовского, В.Ф.Демьянова, А.Б.Куржанского, Ф.Л.Черноусько и других. С математической точки зрения нелинейная задача управления по минимаксному критерию содержит ряд трудных, ' до сих пор не решенных вопросов. В случае, когда в качестве модели процесса торможения рассматривается движение материальной точки по пространственной кривой при наличии трения, минимаксную задачу можно свести к обычной задаче оптимального управления. Решение этой задачи может быть получено только численно, так как уравнения, описывающие поведение управляемой системы нелинейны, а учет технических возможностей приводит к необходимости введения фазовых ограничений на траекторию. Разработкой численных методов решения задач оптимального управления с фазовыми ограничениями занималось большое число исследователей [іі-із] , /зО-Зі] , [34-39] , [Ц-2-^5] .
Ведущая роль в решении этой проблемы принадлежит советским ученым - Н.Н.Моисееву, Ф.ЛЛерноусько, Р.II.Федоренко и другим. В основу алгоритма решения задачи оптимизации параметров тормозного участка положен метод "последовательной линеаризации", предложенный Р.П.Федоренко.
Диссертация состоит из трех глав.
Первая глава носит вводный характер. В ней рассмотрены основные технические проблемы, связанные с проектированием тормозных устройств пневмотранспортной системы. Проанализирована работа применяющихся ныне тормозных устройств, приведены характеристики основных параметров, влияющих на процесс торможения, рассмотрен новый тип тормозного участка -фрикционный участок криволинейной формы. В этой же главе рассмотрена простейшая математическая модель движения контейнера на участке указанного типа.
Во второй главе поставлена и решена задача о выборе оптимальной формы тормозного участка. Эта задача формулируется, как задача оптимального управления при наличии ограничений на фазовые координаты. Решается она численным путем. В главе дано описание численного метода решения поставленной задачи, разобраны вопросы вычислительной технологии, имеющие важное значение для успешной реализации метода, а также приведены примеры решения для характерных исходных данных.
В третьей главе рассматривается более сложная математическая модель движения контейнера по тормозному участку. Здесь контейнер рассматривается, как твердое тело, массы ходовых тележек контейнера считаются пренебрежимо малыми.
Для оптимальных кривых, полученных во второй главе проведено сравнение результатов расчета по двум моделям, причем в широком диапазоне менялись геометрические размеры контейнера, а также для имитации различных случаев загрузки и его моменты инерции. В большинстве случаев точечная математическая модель правильно отражает процесс торможения и может быть использована для расчетов конкретных систем.