Содержание к диссертации
Введение
ГЛАВА I. Состояние вопроса 19
1.1. Краткая история развития подкраново-подстропиль-ных систем. Современное состояние 19
1.2. Особенности работы ППФ 29
1.3. Основные недостатки'существующих.методов расчета систем типа ППФ 32
1.4. Современное состояние теории местных напряжений 35
ГЛАВА 2. Анализ и уточнение расчетных. схем и методов. статического расчета 39
2.1. Общие соображения. Задачи главы 39
2.2. Приближенный метод статического расчета 42
2.3. Горизонтальные нагрузки и кручение подкранового. пояса 53
2.4. Точные методы расчета 64
2.5. Учет жесткости узлов 72
2.6. Расчет по деформированной схеме .77
2.7. Анализ.проведенного исследования и основные вы -воды .78
ГЛАВА 3. Тонкостенный. стержень.как. система. плоских полос .88
3.1. Геометрические характеристики.
3.2. Изгиб
3.2.1. Общие выражения для напряжений
3.2.2, Статические моменты 91
3.2.3, Потоки касательных усилий 97
3.2.4, Центр изгиба ...100
3.2.5, Нулевые точки 107
3.2.6, Напряжения 109
3.3. Кручение .118
3.3.1, Общие замечания,,118
3.3.2, Обобщенная секториальная площадь ,,120
3.3.3, Прямое построение эпюры главных обобщенных оекториальных площадей. Определение нулевых . точек 124
3.3.4, Геометрические характеристики , 127
3.3.5, Касательные усилия ...131
3.3.6, Нулевые точки 134
3.3.7, Напряжения 135
ГЛАВА 4. Теория местных напряжений в стержнях с . двухсвязным поперечным сечениж 138
4.1. Уточненные усилия взаимодействия 138
4.2. Расчетные размеры поясов 142
4.3. Напряженное состояние подкрановой стенки при . центрально приложенной нагрузке 150
4.4. Влияние экоцентрисоитета нагрузки 155
4.5. Учет влияния подкреплений 159
4.6. Напряженное состояние пояоов .176
ГЛАВА 5. Исследование влияния местных напряжений на . напряженное состояние ППФ ...185
5.1, Предварительные замечани 185
5.2. Цель, объекты и метод исследования 190
5.3. Результаты исследования 193
Основные выводы и рекомендации 203
Литература 209
- Особенности работы ППФ
- Горизонтальные нагрузки и кручение подкранового. пояса
- Центр изгиба
- Напряженное состояние подкрановой стенки при . центрально приложенной нагрузке
Особенности работы ППФ
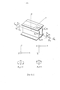
Основные особенности работы рассматриваемых систем и, в частности, ППФ определяются тем обстоятельством, что, будучи внешне выполнены по типу, в общем, плоскостных конструкций (если рассматривать их как систему стержней), они в действительности предназначаются для пространственной работы и могут эту работу обеспечить. Последнее достигается тем, что непосредственно воспринимающие локальные (например, крановые) нагрузки элементы - ездовые пояса - выполняются в виде стержней, способных равноценно работать на изгиб в двух плоскостях и сопротивляться деформациям закручивания. Так как решить такую задачу с помощью стержней открытого профиля практически невозможно, то естественно возникает необходимость выполнения этого элемента в виде стержня с двухсвязным поперечным сечением. Остальные элементы системы - неездовые пояса, решетка - выполняются обычно в виде стержней открытого профиля, преимущественно сварных двутавров. Необходимость всемерного уменьшения деформаций ездовых поясов заставляет выполнять их неразрезными на весь пролет системы, что, в общем, способствует и повышению общей жесткости последней. Основные геометрические параметры и, в частности, высота конструкции в большинстве случаев определяется общим компоновочным решением и условиями экономии материала. Так, например, в ППФ даже вне зависимости от величины пролета, высота конструкции должна обеспечивать размещение и нормальную работу мостового крана. Указанные особенности, а также и то, что оптимальная с экономической точки зрения высота решетчатых конструкций да еще при неразрезности, по крайней мере, одного пояса всегда заметно превышает минимально необходимую по жесткости, делает возможным успешное использование для основных элементов системы сталей СЕЛ и СЕЛ.
Поэтому характер работы таких систем очень существенно отличается от работы схожих по геометрической схеме плооких конструкций и определяется следующим: I) от лежащих в силовой плоскости внешних нагрузок система работает как плоская на общий изгиб и поперечные силы. Нераз-резность ездового пояса при этом снимает часть изгибающих моментов с системы как таковой. Эта часть воспринимается ездовым поясом как неразрезной балкой на упругих опорах. Последними являются примыкающие к этому поясу узлы, испытывающие вертикальные смещения. Чем больше относительная жесткость ездового пояса (по отношению к общей изгибной жесткости системы), тем большую долю изгибающих моментов он берет на себя. Поэтому излишнее развитие этого пояса может оказать неблагоприятное влияние на распреде ление усилий вплоть до того, что в некоторых случаях увеличение сечения может просто "не успевать" за возрастанием приходящейся на него доли изгибающего момента; 2) нагрузки (или их составляющие), не лежащие в силовой плоскости, но действующие вертикально, также приводят к общему изгибу системы, сопровождающемуся закручиванием ездового пояса; 3) горизонтальные нагрузки (например,торможение кранов) вызывает горизонтальный изгиб пояса, сопровождающийся кручением; 4) воздействие подвижных нагрузок при их внеузловом расположении вызывает дополнительный изгиб ездовых поясов (местный изгиб); 5) оложность конструирования узлов примыкания решетки к ездовым поясам заставляет обычно центрировать элементы решетки не на ось пояса, а с некоторым эксцентриситетом.
Это приводит к дополнительному изгибу ездового пояса; 6) локальные воздействия подвижных нагрузок (давления колес крана) вызывают в элементах ездовых поясов дополнительные (местные) напряжения, которые могут существенно изменять картину напряженного состояния по сравнению с традиционными представлениями; 7) наличие подкрепляющих элементов (диафрагм, ребер жесткости и т.п.) также оказывает заметное влияние на распределение напряжений, в основном, в ездовых поясах. Тот же эффект вызывают и детали конструкции узлов. Указанные особенности существенно усложняют теоретический анализ (расчет) силового и напряженного состояния конструкции, вплоть до того, что некоторые из этих особенностей попросту не учитываются из-за отсутствия на сегодня достаточно разработанных приемов и методов.
Горизонтальные нагрузки и кручение подкранового. пояса
В цитировавшемся выше "Руководстве по проектированию стальных подкрановых конструкций" Г?Л предлагается при расчете комбинированных систем, в частности, подкрановых ферм и ППФ, определять усилия в подкрановых поясах от горизонтальных нагрузок, а также от кручения как для однопролетных балок, считая за пролет последних полный пролет конструкции. Такой подход можно считать в определенной мере оправданным лишь в случае расчета подкрановых ферм с ездой по верхнему поясу при условии, что нижний (растянутый) пояс не раскреплен из своей плоскости горизонтальными связями или эти связи имеют очень небольшую горизонтальную жесткость. В противном случае, а также во всех случаях расчета ПЇЇФ, с иелыо снижения соответствующих расчетных усилий в подкрановом поясе, а также с пелью приближения расчетной схемы к действительной пелесообразно учесть работу решетки. Этот учет можно выполнить приняв, что в местах присоединения решетки к ездовому поясу последний имеет упругие опоры, оказывающие сопротивление как горизонтальным омещениям соответствующих поперечных сечений, так и их повороту вокруг продольной оси. Такой подход значительно более правильно учтет фактическую работу конструкции при горизонтальных и несимметричных вертикальных нагрузках. Рассматривая соответствующие смещения пояса (рис.2.3) можно отметить, что при несимметричных вертикальных нагрузках схема работы системы может быть просто разложена на изгиб в вертикальной плоскости и на кручение пояса, сопровождаемое изгибом и кручением решетки. В случае же воздействия горизонтальных сил схема смещений существенно усложняется: изгиб пояса из плоскости конструкции сопровождается его закручиванием, а кручение пояса сопровождается его горизонтальными смещениями, т.е. горизонтальным изгибом. При этом оба смещения ( Az и Г по рис.2.3) имеют при разложении воздействия на составляющие разные знаки. Это должно привести к дополнительному снижению расчетных усилий в поперечных сечениях ездового пояса по сравнению со случаем рассмотрения его как однопролетной балки. Характеристики упругих опор, имитирующих работу решетки, могут быть определены следующим образом.
В зависимости от условий раскрепления второго пояса, закрепление в нем элементов решетки может считаться защемленным или упругим. В случае ШІФ, верхние пояса которых соединены со стропильными фермами, связями, в противодействии смещений которых участвуют также и элементы кровли, можно считать, что соответствующие концы решетки защемлены. При свободном от закрепления поясе его смещения от воздействий решетки будут определяться крутильной жесткостью этого пояса, в соответствии с чем на схемах рис.2.4 вместо полных защемлений следует считать упругие. В случае полных защемлений отпорности решетки при единичных линейном и угловом смещениях соответствующих поперечных сечений ездового пояса для узла Ші можно представить так еоли под ФПРЛ понимать сумму, "проекций" на ось " Ч " моментов инерции всех элементов решетки, сходящихся в узле Л, у относительно осей, лежащих в плоскости хи. . При т, элементах і где: oi\ - угол наклона стержня к продольной оси ездового (Г пояса. Если Cfu , Jkv , ScO - соответствующие моменты инерции ездового пояса, то относительные отпорности при горизонтальном изгибе и кручении Последние величины должны быть использованы при вычислении матрицы коэффициентов (удельных перемещений) уравнений пяти моментов (при расчете на изгиб) или уравнений пяти бимоментов (при расчете на кручение). Уравнения же решаются на ЭВМ по стандартным программам. Указанный подход веоьма существенно изменяет картину распределения усилий в ездовом поясе.
В частности изгибающие моменты при обычных соотношениях размеров и жесткостей пояса и решетки уменьшаются, в среднем, вдвое. Расчетные значения крутящих моментов остаются, в общем, того же порядка, но характер их эпюр меняются очень существенно, вплоть до изменения знаков. Кроме того, при учете работы решетки значительные величины крутящих моментов концентрируются в загруженных панелях. В остальных же панелях они уменьшаются очень заметно. На рис.2.5 в качестве примера показаны расчетная схема и эпюры изгибающих №и и крутящих Мое/ моментов в ездовом поясе ППФ пролетом 150 м, полученные опытными расчетами по "Руководству" Гтч! и по предлагаемой методике. Загрузка осуществлена тормозными усилиями четырех кранов грузоподъемностью 200/50 кН.
В данном случае расчетный изгибащий момент М снизился на 48%. Однако расчетное значение крутящего момента (максимум в узле № 6) повысилось с 13,89 кН»м до 16,81 кН.м, т.е. на 21%. В данном примере особенно интересно отметить, что в большом количестве свободных от нагрузки панелей пояса крутящие моменты при расчете разными методами имеют разные знаки. Это объясняется особенностями деформации пояса при учете работы решетки, показанными на рис.2.3, когда при кручении пояс испытывает и горизонтальный изгиб, превращающий его упругую ось в кривую с различными на разных участках знаками кривизны, а следовательно и с различными знаками углов закручивания. Возможная в принципе схема такой деформации показана на рис.2.6. Полученные в результате предыдущего расчета значения "опорных" (узловых) изгибающих моментов Mm и биомоментов B-L в
Центр изгиба
В соответствии с рис.3.8 положение иентра изгиба Оц поперечного сечения можно определить из двух условий, выражающих отсутствие кручения при: - изгибе поперечной силой ( ч сматривать как выражения, устанавливающие связь "между координатами центра изгиба и положениями нулевых точек, Рассмотрим совместно с рис.3.8 еще рис.3.9, на котором изображен стержень открытого профиля, полученный из представленного на рис.3.8 путем разреза нижнего пояса в точке с координатой Z = Z . Статические моменты Sz0 выражаются по формулам рис.3.5, а статические моменты Зи0 приведены на рис.3.10. Поэтому площади Rxi выражаются по (3.15) с заменой в них Z2 на 7 , а площади эпюр Suo можно представить так Здесь также соответствующие суммы подчиняются условиям (3.18), т.е. не зависят от выбора разреза. Следовательно формулы (3.16) и (3.17) останутся в силе и для вычисления равнодействующих K-L0») , если в правые части их ввести Ru-L и RZL . Через последние величины можно представить координаты пентра изгиба стержня с разрезом в следующем виде Пусть в пентре изгиба Ou стержня замкнутого оечения прикладываются последовательно поперечные силы Q.u=AtJ и Q2 = д) Сделаем в нижнем поясе разрез в точке z = Z . Тогда полученный таким образом стержень открытого профиля (рис.3.9) будет испытывать кручение соответствующими моментами где мы предположили, что Z О и ц 0.
Для ликвидации кручения необходимо приложить постоянные по дуге замкнутой части контура потоки касательных усилий где Q = 8fell - удвоенная площадь, ограниченная средней линией замкнутой части контура. Здесь в соответствии с принятым правилом нижние - знаки относятся к нижнему поясу и правой стенке, верхние- к верхнему поясу и левой стенке. При этом потоки О и a KZ будут подчиняться правилу знаков для касательных напряжений, действуя при Мк 0 против часовой стрелки относительно центра изгиба. Относительный угол закручивания стержня при изгибе его поперечной силой, приложенной вне центра изгиба по [8б]х х) По сравнению с [86] при наличии у стержня консолей мы ввели в правой части интеграл по дуге вместо интеграла по замкнутому контуру. Для iDK это не имеет значения, так как этих напряжений на консолях нет. где Cu - касательное напряжение от изгиба в стержне открытого профиля, которое в случае, например, изгиба силой Q„ определяется второй формулой (3.6), т.е. Тогда s где суммы распространяются на четыре плоских элемента стержня. При суммировании необходимо учесть, что контурное интегрирование проводится в положительном направлении - против движения часовой стрелки, поэтому Так как фактически кручения заїлкнутого профиля нет, то из условия оіф/сіхг 0 получим Совершенно аналогично, рассматривая воздействие поперечной силы 0.x = Д f , получим Путь I. Составим уравнение моментов для действующих на поперечное сечение сил относительно координатных осей. При действии силы Qu = L $ - относительно точки, лежащей на оси 0 , а при действии силы Qx = А Э - относительно точки, лежащей на оси Oz .
Соответственно будем иметь KZ Путь 2. На основании (3.6) и (3.7) для нижнего пояса в точке z = Z потоки касательных усилий соответственно при Qu= дЗ и Qz = дЗ Сравнивая (3.35) и (3.32) можно получить два уравнения относительно координат Чс и Zz нулевых точек, а после определения последних по формулам (3.21) найти и координаты центра изгиба стержня с двухсвязным поперечным сечением. Разберем этот путь более подробно в следующем пункте. 3.2.5. НУЛЕВЫЕ ТОЧКИ Уравнения (3.34) могут быть использованы и для непосредственного определения положения нулевых точек ис и хг без предварительного вычисления координат центра изгиба. Вводя в них (3.21) и (3.24) получим Полученные формулы (3.34) и (3.39) полностью решают задачу определения положения пентра изгиба и нулевых точек статических моментов в двухсвязном поперечном сечении достаточно общего вида, При этом любое поперечное сечение открытого профиля, получаемое путем соответствующей трансформации рассматриваемого двухсвязного сечения, является частным случаем и все вышеприведенные формулы и уравнения к нему применимы. В приложении 5 приведены примеры расчета стержней и, в частности, определения их геометрических характеристик. После нахождения пентра изгиба и координат нулевых точек вычисления напряжений можно производить по формулам (3.6) и (3.7). Однако в ряде случаев, о которых говорилось во введении, необходимо уметь правильно расчитывать напряжения не в целом стержне,а в его отдельных элементах - плоских полосах, получающихся путем расчленения стержня (рис.3.II). Тогда при рассмотрении какой-либо полосы влияние отброшенных частей следует заменить усилиями взаимодействия с (ос/) , где і - номер узла по рис.3.4.
Кроме того должны быть учтены и усилия X](зо) - равнодействующие каса о тельных напряжений в поперечных сечениях данной полосы. Здесь j -номер полосы (т.е. ее индекс, і = 1,2, 0,0е ). Эти равнодействующие уподобляются при таком подходе поперечным силам в полосе, вызывающим, помимо среза, изгиб последних в плоскостях их наибольших жесткостей. Соответствующий изгибающий момент связан с Х\ (») , как с поперечной силой, обычным дифференциальным соотношением. Потоки касательных усилий на кромках стенок в узлах j& I представляются так: - при изгибе в плоскости хО - при изгибе в плоскости xOz
Напряженное состояние подкрановой стенки при . центрально приложенной нагрузке
При действии сосредоточенной силы Р в срединной плоскости стенки (иентральная нагрузка) усилия взаимодействия, приложенные к кромкам стенки, определяются по схеме рис.4.2. От этой схемы загружения в стенке возникают следующие напряжения: I) элементарные, которые можно определить двояко: - по методу главы 3, - как для эквивалентной балки на основании сказанного в предыдущем пункте Обозначив где в общем случае иг , п,0 и t - функции от оо , можно положить Напряжения (4.26) можно подсчитывать и при расчете целого стержня на том этапе расчета, на котором определяются усилия Отметим, что выражение J по (4.27) отличается от выражения элементарного касательного напряжения, приводимого в [37] . Это объясняется тем, что в [з?] под Jf; понимается лишь напряжение, вызываемое поперечной силой в стенке без учета ее совместной работы с поясами. Они определяются исходя из выражения т.е. предполагается, что работает одна стенка без поясов. Поэтому При этом не учитывается элементарное воздействие усилий Of ,(я ) и о[,йС ) на касательные напряжения. Эти последние входят в состав местных напряжений, что с нашей точки зрения порождает некоторые трудности при вычислениях. Поэтому мы будем определять элементарные касательные напряжения по (4.27) введя затем соответствующие коррективы в местные касательные напряжения; 2) местные от давления р(х) , определяемого по (4.2) с учетом эквивалентной площади поясов. Эти напряжения представляются так - функции влияния (безразмерные напряжения), табулированные в [з?] , где они обозначены с , 6С , 3) местные от скачка элементарных касательных усилий сг,(х) , J2(-X) взаимодействия по схеме рис.4.2. В соответствии со сказанным выше при составлении соответствующих выражений необходимо учесть следующее: - во-первых, что табулированные значения функций соответст вующих местных напряжений в [37] приведены для случая загрузки одной (верхней) кромки полосы. Поэтому если для этого случая функции влияния соответственно то при загрузке обеих кромок они будут с учетом нечетности по и нормальных и четности касательных напряжений выражаться для фибры где первые члены учитывают влияние скачка усилий О , а вторые - скачка усилий q2 ; - во-вторых, что, как ранее говорилось, мы исключили из сово купных местных напряжений, определяемых табулированными в [57] функциями оЦ , р с, , п (в [57] они обозначены оЦ , Щ и ]Л ), элементарные напряжения от воздействия (L и Q% . Поэтому в нашем понимании функции местных напряжений получают форму Путем соответствующего пересчета вычислены значения функпий обо » Ra И fo по (4.30) для случая загрузки одной верхней кромки. Они приведены в приложении 2; - в-третьих, что при различных по модулю значениях а и о , вводя обозначения Ксг = 0їа / С! и представляя местные напряжения при загрузке обеих кромок в форме следует вычислять суммарные функции влияния для фибры и- їх-L по формулам 4) местные от "всплеска" касательных усилий взаимодействия вблизи от места приложения нагрузки. Влияние этого воздействия на местные напряжения приншшиально оценивается также, как и влияние скачка усилий -ь (х) . Соответствующие местные напряжения можно представить в форме где совершенно аналогично тому, что сказано при оценке местных напряжений от скачка о и а , функпии влияния имеют вид (для фибры /L= JULi ) а Асі ,дР иА)Г - функции влияния, табулированные в [з7]. Таким образом, рассмотрев все компоненты местных напряжений при центрально приложенной сосредоточенной силе г , можно записать общее выражение местных напряжений в следующем виде (обозначим местные напряжения верхним штрихом) где коэффициент ! i = С( Ь/ Рэ введен для перевода местных напряжений (4.33) и (4.35), выраженных в долях а / б в Дли Рэ/ б Ь , в которых выражены элементарные (4.26) и местные (4.29) напряжения. Полное напряженное состояние стенки получается путем наложе ния местных напряжений (4.37) на элементарные (4.26). В эксплуатируемых на практике подкрановых конструкциях вполне вероятным является смещение линии действия нагрузки (давления колеса крана) из срединной плоскости стенки, т.е. приложение ее с некоторым эксиентрисситетом "е " (рис.4.5). Согласно действующим правилам [5в1,[?8] это смещение на момент приемки монтажных работ ограничивается величиной в 15 мм. При эксплуатации оно, конечно, может и увеличиться. Наличие экспентрисситета порождает два явления: изменение длины о по (4.3) распределения нагрузки поясом на кромку стенки и возникновение кручения узла сопряжения стенки с поясом, а как следствие этого - изгиб пояса и стенки из своих плоскостей. Что касается первого фактора, то согласно работам БЛ.Броуде L 8 , 9 J он может быть с достаточной точностью учтен путем увеличения условной длины А распределения нагрузки на удвоенную величину экспентрисситета, т.е. путем принятия Второй фактор - кручение узла и связанный с этим изгиб пояса и стенки из их плоскостей, представляет собой значительно более сложную задачу. Применительно к стержням открытого профиля -обычным двутавровым балкам, имеющим по крайней мере одну плоскость симметрии - этой задачей занимались очень многие исследователи [з,2б, 59,60,96 08,110и др. Не вдаваясь в подробности этих работ, следует указать, что их результаты не могут быть распространены на двухсвязные поперечные сечения подкрановых конструкций из-за принципиально различной работы поясов, да, в общем, и стенок, что видно из рис.4.5. Для открытого профиля основной деформацией пояса является кручение, стенка изгибается по одной полуволне. В двухсвязном сечении пояс испытывает изгиб, как опертая по контуру пластинка, а стенка изгибается из своей плоскости по двум полуволнам. единственной известной автору работой, в которой сделана попытка учета рассматриваемого явления для коробчатого двухсвязного сечения (применительно к конструкциям крановых мостов), является работа С.А.Соколова, В.Н.Юшкевича и Ю.Е.Якубовского [81] . При достаточно общих предпосылках, а именно: 1) рельс работает как балка на сплошном винклеровом основании и имеет две упругие опоры в местах расположения ближайших к грузу диафрагм или вертикальных ребер жесткости; 2) подрельсовая стенка и пояс представляют собой пластины, шарнирно опертые по контуру и жестко соединенные друг с другом (неучет податливости сварного поясного шва), авторы построили свое решение, основываясь на работах Ю.А.Шиманского [э?] по изгибу пластин. Изложим их основные результаты в наших обозначениях. Давление, передаваемое рельсом на пояс при приложении нагрузки Р в сечении сх = 0, представляется в виде