Содержание к диссертации
Введение
ГЛАВА I. Внутримолекулярные перегруппировки и методы их описания (Литературный обзор) 6
1. Основные типы внутримолекулярных перегруппи ровок в многоатомных молекулах 6
2. Конформационные переходы в макромолекулах и динамическая структура полимеров 10
3. Теории внутримолекулярных перегруппировок с одной координатой пути перехода 17
4. Теории перегруппировок с несколькими коорди натами путей перехода . 20
Заключение и постановка задачи 24
ГЛАВА II. Теория внутримолекулярных перегруппировок при наличии нескольких одновременных координат путей перехода 26
I. Константа скорости внутримолекулярной перегруппировки при наличии нескольких одновременных координат путей перехода 27
2. Физический смысл трансмиссионного коэффициента в теории мономолекулярных процессов, осуществляющийся одновременно по многим координатам путей реакции 30
3. Энергия активация внутримолекулярной перегруппировки при наличии нескольких одновременных координат путей перехода 37
4. Методика определения критических параметров переходной конфигурации 39
Заключение к главе II . 41
ГЛАВА III. Применение теории кооператишых внутримолекулярных перегруппировок для анализа процесса инверсии 43
І. Расчет констант скоростей инверсии молекул /sJH3 , fi/Ad , РИ5 43
2. Расчет энергетических барьеров инверсных переходов в молекулах />/Н3 , // , РН3 и / 47
ГЛАВА ІV. Применение теории кооперативных перегруппировок для анализа динамической структуры полимеров 55
I. Корреляция, движения бокового радикала и главной цепи 56
2. Поворотные изомерные переходы в главных цепях макромолекул 57
3. Некоторые перспективы применения теории кооперативных перегруппировок 72
Выводы 75
Литература
- Конформационные переходы в макромолекулах и динамическая структура полимеров
- Физический смысл трансмиссионного коэффициента в теории мономолекулярных процессов, осуществляющийся одновременно по многим координатам путей реакции
- Расчет энергетических барьеров инверсных переходов в молекулах />/Н3 , // , РН3 и /
- Поворотные изомерные переходы в главных цепях макромолекул
Введение к работе
Основными формами движения 2-х и 3-х атомных молекул являются внутренние колебания и поступательные и вращательные движения молекул как целого. Характерной и весьма важной особенностью многоатомных молекул, имеющих несколько равновесных конфигураций, является движение в форме внутримолекулярных перегруппировок. Важными примерами таких перегруппировок являются инверсия в пирамидальных молекулах ( /// и др.) и поворотно-изомерные переходы в макромолекулах. Явление инверсии широко используется в квантовых генераторах. Поворотно-изомерные переходы определяют релаксационные явления в полимерах и многие свойства полимерных тел, а в ряде случаев и кинетические особенности реакций с участием макромолекул.
Вследствие этого изучение механизмов молекулярного движения выдвигается в ряд актуальных проблем физики полимеров. Это находит отражение в росте экспериментальных работ и в стремлении к более полному исследованию спектра молекулярных движений в широком диапазоне частот 10 * 10^ гц с привлечением методов низкочастотной Ж спектроскопии, рассеяния нейтронов, микроволновой радиоспектроскопии и люминисцентных и парамагнитных "меток", вводимых в макромолекулы. Однако эти исследования носят разрозненный характер и их результаты обычно не сопоставляются.
Для интерпретации такого комплекса данных на единой теоретической основе существующих феноменологических представлений, основанных на таких усредненных характеристиках вещества как свободный объем, коэффициенты вязкости, диффузии и т.п., недостаточно.
Для успешного развития исследований динамической структуры
полимеров в настоящее время необходимо развитие молекулярно-ки-нетической теории поворотно-изомерных переходов и релаксационных явлений в полимерах.
Цель настоящей работы заключалась в построении теории внутримолекулярных перегруппировок в сложных молекулах и полимерах, описывающей взаимосвязь двух форм движения - колебательного и поворотно-изомерного. В задачу работы входила также апробация теории путем применения ее для описания процесса инверсии в молекулах аммиака, фосфина и применение теории для анализа динамической структуры полимеров, для которых были специально получены экспериментальные данные о частотах колебаний, релаксационных процессах и поворотно-изомерной структуре цепей.
Научная новизна работы заключается в обосновании и построении теории кооперативных внутримолекулярных перегруппировок, идущих при одновременном изменении нескольких внутренних координат. При этом возможность перехода макромолекулы из одной равновесной конфигурации в другую определяется возможностью нужного изменения координат при внутримолекулярных колебаниях. Получены аналитические выражения для константы скорости и энергетического барьера кооперативной внутримолекулярной перегруппировки. На основе экспериментальных данных о колебаниях и релаксационных процессах теория позволяет оценивать параметры критической конфигурации соответствующих внутримолекулярных перегруппировок.
Примеры практического применения теории, выполненные в диссертации, показывают, что она является хорошей базой для исследования динамической структуры полимеров комплексом физических методов, включающих низкочастотную спектроскопию, релаксационную спектроскопию и способы определения равновесных поворотно-изомерных форм макромолекул.
Конформационные переходы в макромолекулах и динамическая структура полимеров
Экспериментальные и теоретические исследования динамики отдельных макромолекул служат основой для понимания физической кинетики полимеров в полимерных телах. В самом общем виде ситуацию можно охарактеризовать так [I2J : структура отдельной макромолекулы определяет весь потенциально возможный набор конфор-мационных переходов, а окружающая среда определяет реализацию некоторых из них. При этом роль межцепного взаимодействия сводится к ограничению амплитуд крутильных колебаний цепи вблизи равновесных конфигураций [13, 14] и к стабилизации определенных конформаций цепи (в особенности, ниже температуры стеклования и в кристаллах).
Основные представления о механизме внутримолекулярной под вижности полимерных цепей были сформулированы еще в 30-40-е годы (см. обзор [15J ). Уже тогда были предложены два основных механизма теплового движения макромолекул: I) механизм накопления малых крутильных и деформационных колебаний (Я.Н.Френкель, СЕ. Бреслер, 1939); 2) механизм свободного и заторможенного внутреннего вращения, связанного с преодолением внутримолекулярных потенциальных барьеров (Г.Кун, Тейлор, 1947).
Работами Волькешптейна, Птицына и Бирщтейн [16, 17] , а также Флори [18] , было показано, что для гибкоцепных полимеров доминирует поворотно-изомерный механизм.
Конформационные свойства и внутримолекулярная подвижность жесткоцепных полимеров изучались в работах Цветкова и его сотрудников [19] . В этих полимерах поворотно-изомерное движение либо полностью отсутствует, либо сильно заторможено и на первое место выступает колебательный механизм теплового движения. Развитию кинетической теории полужестких макромолекул на основе механизма накопления колебаний посвящены работы [20, 21J . Оказалось, что для построения теории динамических свойств таких макромолекул модели гауссовых субцепей (сегментов) недостаточно, так как такая модель не позволяет рассматривать динамику мелкомасштабных высокочастотных движений, атомных групп, малых по сравнению с размерами статистического сегмента цепи и ответственных за релаксационные процессы, проявляющихся в диэлектрической релаксации, ЯМР, деполяризации флуоресценции, а также в высокочастотных процессах ультразвуковой релаксации [15 ] .
Построение адекватной теории этих явлений требует рассмотрения такой модели полимерной цепи, в которой элементарной кинетической единицей была бы не гибкая гауссова цепь, а жесткий элемент. Таким жестким элементом может быть, например, мономерное звено цепи. В [15] отмечается, что "в идеальной строгой теорий релаксационных процессов таким жестким элементом будет являться химическая связь. Этот жесткий элемент должен быть способен к вращению или к колебаниям по отношению к соседним жестким элементам".
С точки зрения теоретического описания связи процессов релаксации с колебательным движением полимерных цепей существенный интерес представляет работа [22 J . В этой работе для описания движения полимерной молекулы в аморфном образце использована система кинетических уравнений, аналогичная уравнениям движения периодического "вязко-упругого" кристалла. При таком описании спектр времен низкочастотной дипольно-эластической релаксации имеет универсальный вид, независящий от конкретной структуры полимера. По аналогии с молекулярными кристаллами, в которых самые низкие частоты акустической ветви связаны с синфазным движением всех атомов, предполагается, что низкочастотная область релаксационного спектра в полимерах соответствует совместному согласованному поступательно-вращательному движению участка полимерной цепи как целого. Такой участок включает 20-30 атомов углерода. Высокочастотная часть спектра обусловлена либо высокочастотными внутриячеичными движениями (например, вращением боковых радикалов), либо несогласованными вдоль цепи движениями (перескоками одной или нескольких атомных групп). Подобные движения групп, включающих 4-6 атомов углерода ответственны за процессы высокочастотной дипольно-радикальной релаксации в полимерах.
Физический смысл трансмиссионного коэффициента в теории мономолекулярных процессов, осуществляющийся одновременно по многим координатам путей реакции
В 1 настоящей главы величина іД+ определялась для случая, когда только f}. -ая координата изменяется в направлении процесса, а остальные координаты изменялись произвольным образом (формула 23).
В настоящем параграфе рассматривается случай, когда несколько координат одновременно изменяются в направлении процесса. Ниже дается вывод выражений для средней скорости изменения координат путей процесса и константы скорости внутримолекулярной перегруппировки, при наличии трех ( П = 3) одновременных координат путей перехода. определяется следующим образом: где средняя скорость изменения координаты 4. в направ-лении процесса, W ,, - совместная плотность вероятности п коррелированных импульсов (см. (18)),
В теории абсолютных скоростей реакций [43] важное место отводится проблеме трансмиссионного коэффициента. Необходимость введения этого коэффициента в выражение для константы скорости процесса обусловлена тем, что не все системы, обладающие достаточной энергией для достижения переходной конфигурации, в действительности переходят в конечное состояние. Если реакция протекает адиабатически, то система, находящаяся на вершине энергетического барьера (рис. 8) имеет равную вероятность перейти в стабильные состояния I и П. Из общего числа систем, участвующих в переходе I — П при тепловом равновесии лишь доля.может завершить переход, не возвращаясь в исходное состояние. Эта доля / называется трансмиссионным коэффициентом. В книге [43J отмечается, что величина J зависит от взаимных переходов поступательной и колебательной энергий, то есть от кривизны ложбины, вдоль которой протекает путь реакции на поверхности потенциальной энергии системы.
В рассматриваемом нами случае, когда система обладает многими колебательными степенями свободы и несколькими одновременными координатами путей перехода, смысл трансмиссионного коэффициента имеет существенную специфику. В этом случае, если многоатомная молекула приобретает необходимую для перехода энергию, действительная возможность реализации перехода зависит от степени корреляции импульсов, сопряженных с координатами путей перехода.
Вопрос об определении трансмиссионного коэффициента для случая двух одновременных некоррелированных координат путей перехода ранее рассматривался Слэтером в работе [44] . В этой работе трансмиссионный коэффициент определялся в виде К= тг где 1 - - jj1 L p ( Д ) 0/ / - средняя скорость изменения координат, когда обе координаты изменяются в направлении процес су «о Qa 0i= J f Іг P (VU , средняя скорость изменения координаты [. , когда вторая координата изменяется произвольным образом.
Смысл трансмиссионного коэффициента в этом случае виден из рис. 9 [44] . На этом рисунке молекула, совершающая переход, представляется точкой фазового пространства, пересекающей гра-ницу Q - 4. с положительной скоростью с %. t а границу %-cvlo с положительной, но весьма малой скоростью % Если точ-ка имеет отрицательную скорость с\х , то она может быстро пересечь границу с\ = о (как показано стрелкой на рисунке). Этот случай соответствует дезактивации молекулы.
В нашем случае трансмиссионный коэффициент дается в виде отношения средних скоростей изменений координат перехода, определяемых формулами (53) и (23).
Энергия активация внутримолекулярной перегруппировки по кинетической модели определяется следующим образом: где X - константа скорости перегруппировки, 7" абсолютная температура.
Подставляя в (62) выражение для X (33) и учитывая, что предэкопоненциальныи множитель слабо зависит от температуры, получим энергию активации для внутримолекулярной перегруппировки, при наличии п одновременных координат путей перехода
В теории Слэтера вводится фиктивная координата пути процесса, как линейная комбинация нормальных координат. Однако для многих реальных систем определить эту координату очень трудно. В таких случаях координату пути процесса обычно отождествляют с одной из внутренних координат. Естественно, что это приводит к слишком грубым оценкам констант скоростей и энергетических барьеров внутримолекулярных перегруппировок.
В I изложена теория внутримолекулярных перегруппировок, при наличии многих координат путей процесса, когда критическая конфигурация задается совместной плотностью вероятности всех критических значений внутренних координат. В настоящем параграфе излагается методика определения критических значений внутренних координат на основе экспериментальных значений констант скоростей и энергетических барьеров переходов.
В принципе, если имеются л независимых экспериментальных X для молекулы и ее изотопозамещенных, то можно определить критические значений координат перехода (%0ЛЛо " )« Практически это конечно не выгодно. Однако можно поставить задачу определения наиболее оптимального варианта %L ] ,% \- - "J , которым тоже можно описывать процесс, если имеется два эксперимента, т.е. имеется у молекулы и Уу одного из изотопозамещенных молекул. Процедура определения наиболее оптимального варианта критической конфигурации заключается в следующем.
Расчет энергетических барьеров инверсных переходов в молекулах />/Н3 , // , РН3 и /
Основными формами движения малых молекул являются внутримолекулярные колебания и вращательные и поступательные движения молекул как целого. Важной особенностью макромолекул является тепловое движение в форме поворотно-изомерных переходов атомных групп полимерных цепей. Этот вид внутримолекулярной подвижности в значительной мере определяет релаксационные явления, физико-химические и физико-механические свойства полимерных тел, а во многих случаях и кинетические особенности реакций с участием макромолекул. Очевидно, что полное решение задачи описания динамической структуры полимеров должно основываться на единстве и взаимосвязи.внутримолекулярных колебаний и поворотно-изомерных переходов.
Поскольку конформационные переходы существенно кооперативны, представляется перспективным их анализ с помощью теории, изложенной во второй главе диссертации. Это обусловлено тем, что теория естественным образом связывает параметры внутримолекулярных колебаний (частоты, силовые постоянные) с характеристиками релаксационных процессов (константы скорости, энергии активации). Кроме того, теория позволяет подойти к определению такой важной характеристики динамической структуры, как параметры переходной конфигурации.
В настоящей главе анализируются возможности теории кооперативных внутримолекулярных перегруппировок для анализа основных типов теплового движения макромолекул: боковых радикалов и главных цепей.
Корреляция движения бокового радикала и главной цепи
В работах, посвященных изучению движения боковых полярных групп в полимерах типа ( — СХ—СК ) методом диэлектри-ческой релаксации, имеются указания на то, что это движение не является полностью локальным, а коррелированно с движением главной цепи [12, 49 ] В связи с этим, настоящий параграф посвящен выяснению вида переходной конфигурации для случая, когда поворотно-изомерный переход в боковой цепи определяется двумя координатами путей перехода - углом внутреннего вращения бокового радикала f и изменением прилегающего валентного угла ( главной цепи (см. рис. 12а). Задача решалась на основе экспериментальных данных о частотах колебаний и энергии активации процесса диэлектрической релаксации виниловых полимеров, имеющихся в литературе.
Для случая двух координат путей перехода формула для энер-гии активации поворотно-изомерного перехода (63) принимает вид: где Р0 и dc - критические значения координат путей перехода. Типичные значения частот и форм колебаний и силовых постоянных были взяты из литературных данных [50] и приведены в таблице XI. Вычисленные с их помощью значения величин, входящих в формулу (76), также приведены в таблицах XI и ХП. Критические значения угла внутреннего вращения fQ и валентного угла 0 были определены с помощью формулы (67), применяя "методику определения критических параметров", изложенную в 4, гл. П. С помощью формул (68), внутренняя координата -чр была выражена через изменение валентного угла . Энергия активация поворотно-изомерного перехода в боковой цепи виниловых полимеров [51] за вычетом вклада межмолекулярных взаимодействий может быть принята равной 2,39 ккал/моль.
Подставляя в формулу (76) необходимые значения величин из таблицы XI и Ш и значения (J0 = 2,39 j 9-}, находим критическое значение второй координаты пути перехода о(0 - 7. Затем, используя соотношения (68), находим критическое значение угла внутреннего вращения бокового радикала fo - 20.
Результаты проделанного расчета показывают, что локальные движения бокового радикала в виниловых полимерах коррелированн с движением главной цепи и поворотно-изомерный переход боковой группы происходит при одновременном значительном изменении валентного угла oL главной цепи. Кооперативность перехода в данном случае обусловлена значительной величиной коэффициента корреляции Z (табл. XI).
Следует заметить, что полученный результат довольно хорошо согласуется с выводом работы [49] . Авторы этой работы на основе расхождений между величинами энергетических барьеров, вычисленных в модели парных атом-атомных взаимодействий и определенных экспериментально, пришли к заключению, что поворотно-изомерные переходы боковых групп в виниловых полимерах требуют "раскрытия" валентных углов главной цепи. При этом хорошее согласие расчетных и экспериментальных данных достигается при изменении угла на величину порядка 20 [49] .
Поворотные изомерные переходы в главных цепях макромолекул
В двух предыдущих параграфах было рассмотрено применение теории для анализа классических проблем физической кинетики полимеров. В настоящем параграфе кратко рассмотрены некоторые новые задачи, требующие для своего решения детального анализа динамической структуры объектов на основе развитой в работе теории кооперативных внутримолекулярных перегруппировок.
В последнее время для объяснения высокой эффективности ферментативного катализа привлекаются представления о снижении энергетических барьеров химических реакций путем одновременной синхронной атаки нескольких групп [62] # Эти представления основаны на том, что элементарные акты химических реакций должны удовлетворять принципу "наименьшего движения" [63] . Согласно этому принципу для перехода в активированное состояние недостаточно только ориентировать реагирующие группы и сообщить им необходимую энергию. Необходимо также, чтобы эти группы синхронизировали свое движение в нужном для процесса направлении. Полагают [62] , что именно синхронизацию движения атомных групп в "продуктивных" фермент-субстратных комплексах обеспечивает участие оптимального числа ядер и приводит к значительному снижению энергии активации процесса. При этом возможность влияния колебаний атомных групп друг на друга в ферментах объясняют наличием "орбитального перекрывания" [62] . Следует однако заметить, что недиагональные коэффициенты Кп в матрице потенциальной энергии колебаний молекулы, как раз и являются количественной мерой "орбитального перекрывания". Вследствие этого коэффициенты корреляции в теории кооперативных перегруппировок естественным образом могут учитывать синхронизацию движений атомных групп в фермантах, обуслов
ленную орбитальным перекрыванием. Поскольку теория связывает энергетические барьеры кооперативных внутримолекулярных перегруппировок с коэффициентами корреляции и критическими значениями координат путей перехода, она может оказаться полезной для анализа на единой основе комплекса данных, получаемых методами спиновых меток, низкочастотной спектроскопии, Мессбаэровской спектроскопии, а также путем расчета поверхностей конформаци-онной энергии.
Теория может быть использована для анализа влияния химической модификации полимеров на константы распада химических связей в главных цепях макромолекул. Необходимость такого анализа возникает в связи с появлением работ, посвященных поиску способов увеличения стойкости полимеров к действию лазерного излучения, путем введения боковых "защитных" групп. Механизм защитного действия заместителей практически не известен. Однако ясно, что при этом модифицируется колебательный спектр и, следовательно, вся динамическая структура макромолекулы. По-видимому, анализ влияния заместителей на величину константы скорости распада по формуле (33) в этих случаях может способствовать выяснению механизма стабилизации полимеров.
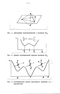
Представляется перспективным применение теории для исследования различных перегруппировок в координационной сфере мета ллокомплексов. Согласно последним данным [64] , подобные внутрикомплексные перегруппировки представляют основу для понимания каталитических свойств комплексов переходных металлов, в том числе катализаторов Циглера-Натта. Однако квантовая химия пока еще не может количественно рассчитывать профили потенциальной энергии и траектории движения атомов при различных перегруппировках в координационной сфере металлокомплексов [64J . В то же время кооперативный характер и коррелированное движение атомных групп создают благоприятные предпосылки для расчета констант скоростей и энергетических барьеров таких перегруппировок с помощью предложенной теории. Благоприятньм объектом для проведения расчетов может быть, например, перегруппировка Бер-ри [б5] (см. схему)
Как видно из схемы, перегруппировка представляет собой синхронное перемещение лигандов и (Зд в плоскости #г и лигандов 2 и 3 в плоскости X f с сохранением симметрии CS(y комплекса в ходе всего процесса.