Содержание к диссертации
Введение
1 Глава 1. Базовые понятия и определения . 25
1.1 Необходимые определения 25
1.2 Линейные и аффинные преобразования 28
1.3 Модели компактного представления бинарного дерева - виды диаграмм 30
1.4 Бинарные диаграммы решений - формальный подход 37
1.5 Бинарные диаграммы решений с разделением общих частей для функций с несколькими выходами 39
1.6 Минимизация не полностью заданных функций 40
1.7 Выводы 41
2 Глава 2. Линейные и аффинные преобразования переменных и обоснование алгоритмов 43
2.1 Проблема сокращения размера бинарных диаграмм с помощью линейных и аффинных преобразований 43
2.2 Линейные и аффинные преобразования переменных и сокращение размера бинарных диаграмм решений 44
2.3 Матричное задание линейных и аффинных преобразований 47
2.4 Теорема 2.1 50
2.5 Теорема 2.2 52
2.6 Анализ влияния линейных и аффинных преобразований над соседними переменными на бинарное дерево 53
2.7 Идея алгоритма сокращения размера БДР. 58
2.8 Выводы 59
3 Глава 3. Построение алгоритмов 60
3.1 Построение алгоритма 60
3.2 Алгоритм упорядочения дерева. 64
3.3 Модифицированный алгоритм (А1) 65
3.4 Метод двухуровнего перебора (А2) 66
3.5 Алгоритм выявления симметрии (A3) 67
3.6 Алгоритм однородности (А4) 67
3.7 Выводы 69
4 Глава 4. Теоремы и экспериментальные оценки эффективности алгоритмов 70
4.1 Число шагов алгоритма однородности 70
4.2 Пример сокращения БДР функции XOR5 алгоритмом А4 73
4.3 Экспериментальная оценка уменьшения бинарных диаграмм 75
4.4 Эффективность работы алгоритмов и их совокупностей на функциях с одним выходом для различного числа входящих переменных 77
4.5 Функции с несколькими выходами 77
4.1 Описание программного комплекса 80
4.2 Выводы. 81
Заключение 83
Литература 85
Приложения 96
Исходные тексты программ 96
- Модели компактного представления бинарного дерева - виды диаграмм
- Линейные и аффинные преобразования переменных и сокращение размера бинарных диаграмм решений
- Метод двухуровнего перебора (А2)
- Эффективность работы алгоритмов и их совокупностей на функциях с одним выходом для различного числа входящих переменных
Введение к работе
Состояние проблемы:
Одной из центральных задач при проектировании оборудования является задача оптимизации размера схем. Уменьшение размера схем на этапе проектирования устройств позволяет, с одной стороны, экономить средства на стадии производства, а с другой стороны, может привести к значительному ускорению процесса вычислений за счет уменьшения времени задержки. Диаграммы решений (ДР) — это структуры данных, позволяющие эффективно представлять большие дискретные функции в терминах пространства и времени.
Интерес к диаграммам решений возрос после публикации [1], причем как к оригинальным диаграммам решений для функций-триггеров, где большинство исследователей ссылались на [2] и [3], так и для функций с несколькими выходами на [4]. ДР стали структурой данных, полученной сокращением деревьев решений (бинарных деревьев), с помощью использования общих изоморфных поддеревьев и удаления избыточной информации из деревьев решений для данной функции. Бинарные деревья были впервые представлены в диссертации [5] о некоторых проблемах в теории дискретных множеств, защищенной в 1935 году в Сорбонне.
Разложение Шеннона имеет вид:
/ = *,Л=о V *іЛ,=1 > 0 ^' ^ и)-
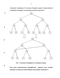
Рассмотрим бинарное дерево (рисунок 1), где на каждом узле применяется разложение Шеннона по одной из переменных. Таким образом, функция разбивается на несколько подфункций, а дерево соответственно на несколько поддеревьев.
Пунктиром обозначается нулевое значение переменной, а сплошной линией — единичное. На каждом уровне присутствует только одна переменная, по которой и выполняется разложение функции (рисунок 1).
АХ ХА
о о
Рис. 1. Бинарное дерево
Для определения значения функции, заданной бинарным деревом для конкретного набора переменных, проходится путь от корня к оконечной вершине, следуя значениям соответствующей переменной. Бинарное дерево является достаточно громоздким средством графического представления булевой функции, обладая при этом некоторой избыточностью. Для уменьшения количества узлов применяются
следующие сокращения. В исходном бинарном дереве отождествляются изоморфные подграфы, эта процедура показана на рисунке 2.
(«
&
Рис. 2. Удаление изоморфности из бинарного дерева.
Если после отождествления изоморфностей сократить узлы, которые указывают на один узел (таким образом, как показано на рисунке 3),
Рис. 3. Сокращение узлов, оба выхода которых указывают на один и тот же
узел.
в результате получится бинарная диаграмма решений (БДР).
Бинарные диаграммы решений являются эффективным способом манипуляции большими структурами данных с целью их оптимизации, верификации и вычисления различных характеристик.
Основной недостаток приложений, базирующихся на бинарных диаграммах решений, - это то, что структуры данных являются зависимыми от порядка переменных, а также что для некоторых функций не существует эффективного представления, например для булевских умножений. Для решения проблемы оптимального порядка переменных были написаны специальные алгоритмы, частично сокращающие перебор полного множества вариантов. Для решения проблемы представления
умножения и для повышения общей компактности были предложены несколько расширений базовой структуры двоичных диаграмм решений -например диаграммы с подавлением нуля (ZBDD)[89]. При этом продолжается также поиск других путей сокращения размера бинарных диаграмм решений. Линейные преобразования были очень обнадеживающей концепцией, так как непосредственно структуры данных остаются неизменными, а изменяются (перекодируются) только входные переменные, причем для сохранения результирующих значений изменяется и сама функция. Также следует отметить, что даже такая значительно более простая задача, как нахождение оптимального порядка переменных, является NP-полной [12]. В случае с линейными преобразованиями ситуация осложняется тем, что количество вариантов линейных преобразований по сравнению с перестановками входящих переменных существенно больше. В работе «Линейные преобразования и точная минимизация BDD» Wolfgang Gunter и Rolf Drechsler (1998) [7] применили расширение метода перестановок (permutations) линейными преобразованиями и получили более хорошие результаты минимизации бинарных диаграмм решений. Однако, несмотря на высокую эффективность, алгоритм имеет очень большую сложность. Идея заключается в том, чтобы найти такое линейное преобразование, при котором сложность реализации преобразования и видоизмененной функции будет меньше, чем исходной. Тогда для нахождения оптимального линейного преобразования вместо преобразований над таблицей функции, что обычно и делается в спектральных методах, преобразуются только входные переменные.
То есть если рассмотреть исходный вектор переменных X, линейное преобразование Z, то в результате получим схему преобразования, показанную на рисунке 4.
X )Y
Рис. 4. Иллюстрация преобразования переменных и изменения
функции.
Таким образом, имеем:
AX = Y,
где Y- это преобразованный вектор переменных, а А - матрица, задающая
линейное преобразование L. Если исходная функция была /, то формула
f\Y) = A(f(X)) будет задавать измененную функцию.
Для реальной практической ценности этого метода минимизации в результате сложность представления измененной функции и матрицы преобразования должны быть меньше сложности представления исходной функции.
Смысл минимизации линейными преобразованиями заключается в поиске наименьшего или приемлемого по размеру (в смысле количества узлов) в бинарной диаграмме решений преобразованной функции по сравнению с исходной БДР. Для получения исходной функции из преобразованной применяется схема, показанная на рисунке 5.
Для задания линейных преобразований используются матрицы размерности пхп вместо матриц размером 2"х2" применяемых в спектральных методах, где п - число входящих переменных. Для некоторых функций при использовании линейных преобразований может
быть получено экспоненциальное уменьшение количества узлов в результирующей бинарной диаграмме решений.
Рис. 5. Схема получения исходной функции из преобразованной.
Этот подход к минимизации интересен простой реализацией результатов вычислений: достаточно преобразовать входящие переменные умножением на матрицу размерности их и и получается значительно
упрощенная схема. Но NP-полнота точных алгоритмов и огромное
«-і количество вариантов р~[(2"-2') [7] линейных преобразований позволяет
/=0
осуществлять линейное преобразование для получения минимально возможной функции (точную оптимизацию) только на функциях с очень небольшим количеством переменных. Поэтому в настоящее время производятся поиски различных эвристических алгоритмов, которые давали бы вполне приемлемые результаты, но имели бы значительно меньшие требования как по времени вычислений, так и по другим требуемым ресурсам.
Для преодоления проблем, связанных с большой размерностью БДР при реализации булевских умножений, и для более компактного представления функций были предложены расширения структуры БДР. Этой области посвящено достаточно много современных работ. Расширениями B,uT(BDD) являются KDD (Kronecker Decision Diagrams)
[6], PKDD (Pseudo-Kronecker Decision Diagrams) [6], ZBDD[89]. Различия
заключаются в следующем:
+ В бинарной диаграмме на каждом узле применяется разложение
Шеннона. При этом кроме объединения изоморфных ветвей применяется удаление узла, если его исходящие ветви указывают на один узел. Другие виды диаграмм решений, используют различные комбинации типа разложения и метода сокращения «вырожденных» узлов, как например, ZBDD (Zero suppressed Binary Decision Diagram - Бинарные диаграммы решений с подавлением нуля). В ZBDD - вместо удаления вершины, у которой исходящие ветви указывают на один узел, применяется удаление узлов, если единичный выход указывает на 0. Этот метод в общем случае хуже, чем в бинарной диаграмме решений (BDD), но значительно лучше в некоторых специальных случаях, например при реализации булевских умножений.
^ Диаграммы решений Кронекера (KDD) являются расширением BDD
путем использования разложений positive Davio Expansion и Negative Davio Expansion. В этом случае на каждом уровне применяется либо разложение Шеннона, либо Davio Expansion, либо Negative Davio Expansion.
Псевдо-Кронекеровские диаграммы решений (PKDD) - расширение KDD, но в этом случае на одном уровне можно использовать разложения
#) positive Davio Expansion и Negative Davio Expansion, либо разложение
Шеннона.
В работе [6] описываются преимущества PKDD над BDD, но при этом опять возникает проблема построения оптимального PKDD. Процесс построения оптимальной псевдо-кронекеровской диаграммы решений сам по себе является процессом оптимизации и для этого требуются большие вычислительные ресурсы. Поэтому при построении PKDD также применяются эвристические алгоритмы. При этом по проведенным
исследованиям на случайных функциях от 15 переменных, размер PKDD
составляет около 65% от базовой функции.
4 В работе [7] описан метод точной минимизации BDD, с
использованием линейных преобразований над входящими переменными. Метод является расширением линейными преобразованиями метода перестановок, и имеет сложность ЛП, где JV = 2" - количество значений функции. Значение N1 является слишком большой величиной, и поэтому применение метода возможно только для функций от небольшого количества переменных (не более 6).
Несмотря на то, что были созданы достаточно эффективные алгоритмы для сокращения размера BDD, они базируются на различных переборах, - осталась открытой проблема построения эвристического логического метода, не базирующегося на различном переборе возможных вариантов. Дело в том, что созданные алгоритмы базируются на методах
4, перестановки и поиска линейных преобразований, но ограничивают их
различными способами, чтобы получить сложность алгоритма, приемлемую для вычислений. То есть, например, в качестве ограничения используется перебор не по всем переменным, а только по нескольким соседним и тому подобное. Но ключевым фактором остается перебор. В данной же работе производится поиск критерия, который позволит
> уменьшить сложность BDD путем поиска преобразований над соседними
переменными. Это приведет к полиномиальной сложности алгоритма относительно размера таблицы значений функции (2"). Для обеспечения возможности полного перебора всех возможных значений для нахождения характерных случаев неоптимальности, исследования при построении критериев производились на функциях небольшого размера (до 4-х переменных).
*
Актуальность проблемы:
Бинарные диаграммы решений (БДР или ROBDD в англоязычной литературе) являются одной из моделей представления булевых функций в виде направленного нецикличного графа и имеют связь с топологией реальных схем.
На практике бинарные диаграммы решений можно реализовать с помощью элементарных мультиплексоров, то есть БДР напрямую отображается в архитектуру аппаратных средства, например программируемые логические устройства и используется на стадии синтеза таких устройств (рисунок 6).
Функция (схема)
Л V
Модель в виде
бинарной диаграммы
решений
Л V
Реализация
«>
Рис. 6. Схема связи функции, модели БДР и реализации
В настоящий момент бинарные диаграммы решений являются одним из базовых элементов в графическом представлении булевых функций. БДР широко применяются во многих современных областях, например при макетировании схем, в верификации, а также в качестве промежуточного формата для генерации схем из VHLD описания (языка высокого уровня). Сокращение размера бинарных диаграмм решений является актуальной задачей, так как уменьшение размера БДР приводит к сокращению размера схем, реализующих различные функции, и, как следствие, ускорению вычислений и значительной экономии элементов (транзисторов и т. п.).
Бинарные диаграммы решений являются эффективным способом манипуляции большими структурами данных. Бинарные диаграммы
решений широко применяются в верификации для задания различных
характеристических функций..
щ Необходимость в исследованиях, направленных на поиск алгоритмов
для сокращения размера БДР, обусловлена отсутствием приемлемых по
сложности точных методов для нахождения минимально возможной
диаграммы. Это связано с тем, что точные алгоритмы для нахождения
минимальной диаграммы, известные на сегодняшний день, использующие
различные фиксированные классы преобразований, очень близки к
полному перебору и не удовлетворяют по сложности возможностям
вычислительной техники для их эффективного использования. Поэтому
производятся поиски эвристических алгоритмов для сокращения размера
бинарных диаграмм решений, которые дают приемлемые по критерию
соотношения сложности к эффективности результаты. В связи с этим
актуальной задачей является построение таких эвристических алгоритмов.
щ) Преобразования над входящими переменными интересны тем, что
преобразования в результате производятся не над таблицей функции, а только над входящими переменными. При этом преобразование является линейным и задается матрицей размером пхп, вместо матриц размерности
2я х 2" t которыми описываются преобразования над таблицей функции, где
п- число входящих переменных. Идея линейного преобразования входных
«)
переменных в задаче уменьшения размера схем заключается в том, что
вычисление исходной выходной функции разбивается на два этапа.
Сначала производится линейное преобразование переменных, после чего
вместо исходной выходной функции схема вычисляет «измененную»
функцию, чтобы получить «правильное» выходное значение. Таким
^ образом f{xl,...,xn) = L[f{xx,...,x„)).
В процессе сокращения бинарной диаграммы решений с помощью линейных преобразований получается линейное преобразование L и
измененная функция /, которая имеет БДР меньшей сложности чем /. Под сложностью при этом понимается количество узлов в БДР.
Ц> На практике использование линейного преобразования имеет смысл
в том случае, если линейное преобразование L и функция / реализуются проще, чем исходная функция /. Если эффективная реализация линейного преобразования на основе двоичных сумматоров имеет удовлетворительное решение, то точная минимизация схем общего вида на основе линейных преобразований затруднена из-за огромного количества
« преобразований, которое быстро растет с увеличением размера схем.
Бинарные диаграммы решений были использованы разработчиками
CAD (САПР СБИС) при построении схем для ПЛИСов в основном на
стадии логической декомпозиции функций. Сейчас декомпозиция
функций, основанная на бинарных диаграммах решений, называется BDS —
что расшифровывается как BDD-based Decomposition System [33]. Также
показано, что этот подход может эффективно использоваться как для
алгебраических, так и для булевых (а также AND-OR и AND-XOR)
декомпозиций. При этом используются бинарные диаграммы решений для
представления и манипуляций булевыми функциями и выполнения
логической декомпозиции.
Кроме того, бинарные диаграммы решений и их производные активно т
применяются в верификации, так как две схемы, заданные в таком виде
можно легко сравнить между собой структурно, в связи с тем что БДР
является каноническим представлением функции.
Теперь рассмотрим некоторые статьи, имеющие отношение к
преобразованию бинарных диаграмм решений с целью уменьшения их
размера. Эта задача является актуальной, так как размер БДР
непосредственно влияет на размер схем, например при построении ПЛИС.
В статье [12] «Использование нижних оценок в процессе динамической минимизации бинарных диаграмм» приводится описание метода нижних
4 оценок для упрощения при оптимизации размера бинарных диаграмм
путем поиска оптимального преобразования. В статье приводится сложность поиска оптимальной последовательности переменных. Она составляет 0(п2*3"), где л — количество входящих переменных. Применение этого метода в среднем на 50% сокращает время поиска оптимального результата. Но с точки зрения сложности 0(3") является
т очень большой величиной, также следует учитывать, что в данном виде
оптимизации применяются только перестановки переменных, без
линейных преобразований. Этот критерий может быть использован только
для сокращения перебора. Если рассматривать оптимизацию как
приведение функции к определенному виду, данный метод не подходит.
В работе [7] «Линейные преобразования и точная минимизация BDD»
* представлен алгоритм нахождения оптимального линейного
преобразования переменных булевой функции для минимизации соответствующей двоичной диаграммы решений. В результатах показано, что бинарные диаграммы могут быть существенно сокращены при использовании линейных преобразований. Так как перестановка входит в подмножество линейных преобразований, то их применение для минимизации бинарных диаграмм увеличивает возможности. Всего
линейных преобразований J~[(2" -2'), что меньше чем 2й!, но существенно
І-0
больше, чем и! (количества перестановок переменных). При этом используется разложение конечного преобразования на более простые, или это можно рассматривать как произведение более простых матриц, каждая из которых соответствует простому преобразованию. Из-за большой сложности вычислений данный алгоритм подходит только для функций, имеющих не более 6 входящих переменных.
В работе [20] "Диаграммы решений в синтезе. Алгоритмы, расширения
и приложения" дан обзор различным видам диаграмм решений. Наиболее
^ популярными являются бинарные диаграммы решений. Но они имеют ряд
недостатков, один из которых - это экспоненциальный размер относительно некоторых функций, например умножителей. Поэтому для решения данной проблемы применяются некоторые другие виды диаграмм решений. В работе описаны различные типы применяемых разложений и редукций, и в зависимости от этого получается определенный тип диаграммы решений. Кроме этого, описываются различные методы минимизации для диаграмм решений, а также понятие World level DD и смешанных диаграмм решений.
"Генетический алгоритм для получения оптимального порядка
переменных" [22] - представлен алгоритм нахождения оптимального
порядка переменных для минимизации бинарных диаграмм решений. Это
^ альтернатива точному алгоритму нахождения оптимального порядка
переменных. При аналогичных результатах с точным алгоритмом на
приведенных тестах он позволяет сократить время поиска в среднем на
50%. Но подход к минимизации двоичных диаграмм решений путем
поиска оптимального порядка переменных уже достаточно хорошо изучен
и из-за меньшего количества вариантов дает менее хорошие результаты,
* чем использование линейных преобразований.
"EXOR преобразования входящих переменных, для разработки эффективных двухуровневых AND/EXOR сумматоров" [40]. В работе показано результатами и доказано, что сумматоры, которые имеют экспоненциальное представление в виде бинарных диаграмм, можно после линейных преобразований представить в виде бинарных диаграмм, сложностью 0(п ).
"Минимизация размера ROBDD неполностью заданных булевых
функций используя строгую симметрию" [39]. Идея работы заключается в
^ том, что симметричные блоки фиксируются, а на остальную часть
применяются обычные перестановки. Метод является достаточно эффективным, но было доказано, что результаты будут хуже, чем при обычных перестановках. Но при этом уменьшается время обработки.
В работе S. Minato [89] представлены бинарные диаграммы решений с подавлением нуля (ZBDD), которые были разработаны как альтернатива классическим двоичным диаграммам решений для случаев, когда бинарные диаграммы оказываются неэффективными. Отличаются от БДР методом применяемой редукции. В бинарных диаграммах узел удаляется, если оба его выхода указывают на одну вершину, а для ZBDD — если единичная ветвь указывает на 0.
"Минимизация бинарных диаграмм, используя линейные
«v преобразования, основываясь на эволюционной технике"[ 18]
Алгоритм работает следующим образом:
Случайно выбираются две переменные и одна из них заменяется на их сумму по модулю два.
Повторение пункта 1 дважды
3. Перестановка двух переменных.
* 4. Линейный сдвиг
Инверсия: в случайно выбранном окне из 8-ми переменных инвертировать порядок переменных в окне.
Удаление линейного преобразования переменных
Точная минимизация: выбор трех переменных и нахождение
оптимального линейного преобразования с использованием точного
алгоритма.
Согласно тестам, алгоритм показывает неплохие результаты за
приемлемое время. Но остается подход упрощенного перебора.
4 «Представление неполностью заданных функций, используя диаграммы
решений Псевдо-Кроннекера» [6]. В этой статье дается определение BDD
(бинарных диаграмм решений), KDD и PKDD. В PKDD в узлах
применяется одно из 3 разложений (S,pD,nD (Формулы 1.1-1.3)). Всего
вариантов для задания PKDD З2""1 и, выбирая для каждого узла одно из
разложений, можно упростить PKDD. В статье рассмотрен эвристический
^ алгоритм для минимизации PKDD для неполностью заданных функций.
Метод заключается в минимизации функции, последовательно используется сначала неполное задание функции, затем производится минимизация построением KDD, затем PKDD.
Поэтому актуальна задача поиска приближенных алгоритмов с некоторым критерием, не основанным на переборах для сокращения
4> размера бинарньк диаграмм решений с помощью линейных и аффинных
преобразований. Цель и задачи исследования:
Целью диссертации является исследование возможностей уменьшения размера БДР путем преобразования ее к некоторому виду на основе разработанных критериев. Для достижения этой цели было произведено
** следующее:
Выделение «базисных» преобразований и изучение влияния этих
преобразований на функцию. Исследование возможностей
преобразования булевой функции с использованием базисных
преобразований.
Разработка критериев, обеспечивающих сокращение размера
т
бинарных диаграмм решений.
Разработка алгоритмов на базе полученных критериев.
Экспериментальная проверка влияния алгоритмов на размер бинарных диаграмм решений.
Обоснование верхней оценки для сложности алгоритма.
Исследование возможностей улучшения критериев и алгоритмов для получения лучших результатов.
Научная новизна:
В диссертации получены следующие результаты, которые выносятся на защиту и характеризуются научной новизной.
Предложен новый подход к сокращению размера бинарных диаграмм решений.
Получены результаты влияния линейных и аффинных преобразований на бинарные диаграммы решений.
Предложен новый подход к сокращению размера бинарных диаграмм решений: преобразования булевой функции путем применения линейных преобразований на входящие переменные с целью приведения функции к определенному виду, удовлетворяющему найденным критериям, с использованием на каждом шаге только преобразования над соседними переменными. При этом научная новизна подхода заключается в том, что размер двоичной диаграммы решений не является основным критерием при непосредственном поиске преобразования функции (работе критерия). Размер являлся базовым критерием для нахождения других более простых и конкретных критериев, задающих вид функции, на основании которых определяется, какое из возможных линейных и аффинных преобразований выбрать на данном этапе, чтобы в результате получить хороший результат.
Создан комплекс программ, реализующий разработанные критерии и алгоритмы.
Найдена верхняя оценка для числа шагов алгоритма. Практическая ценность и реализация результатов работы:
В диссертации построены новые алгоритмы для сокращения размера
бинарных диаграмм решений (БДР). Показано, что можно уменьшить
размер бинарной диаграммы решений путем приведения булевой функции
к виду, удовлетворяющему некоторому критерию, используя линейные и
аффинные преобразования над входными переменными. В ходе
построения результирующего преобразования используются
преобразования только над соседними переменными, что уменьшает число шагов алгоритма. Разработанные алгоритмы можно использовать для выделения подклассов базовых функций, с помощью которых можно задать любую другую булеву функцию, зависящую от соответствующего количества входящих переменных. Разработан комплекс программ для реализации алгоритмов, работающий под операционной системой Windows с использованием средства разработки Microsoft Visual C++. Разработанный программный комплекс используется в учебном процессе на факультете ВМК КГУ при выполнении курсовых и дипломных работ студентов. Результаты также использованы при моделировании цифровых систем в Институте проблем информатики Академии наук Татарстана и в предприятии Сканер. Имеются соответствующие справки о внедрении.. Работа поддержана грантом № 05-5.2-234 из средств Фонда НИОКР Татарстана. Апробация:
Основные положения диссертационной работы докладывались и
обсуждались:
1. Fifth International Workshop on Applications if Reed-Muller Expansions in Circuit Design, August 10-11., Mississippi State University.- 2001.
Четвертая международная конференция «Автоматизация проектирования дискретных схем», 14-16 ноября, Минск.- 2001.
XXVIII International conference (Information Technologies in Science, Education, Telecommunication, Business, autumn session) IT+SE'2001, Yalta, Ukraina.-2001.
XIII Международная Конференция «Проблемы теоретической кибернетики» Казань, 27-31 мая.- 2002.
На семинарах на кафедрах прикладной математики КГУ, теоретической кибернетики КГУ, компьютерных систем и информационной безопасности КГТУ им. Туполева.
Публикации:
По теме диссертации опубликованы 5 работ, из них 4 статьи и 1 тезисы.
Работы приведены в списке литературы.
Структура и объем работы:
Диссертационная работа состоит из введения, четырех глав, заключения и
приложения, изложенных на 139 страницах, содержит 26 рисунков, 1
таблицу, список литературы из 102 наименований.
Диссертация состоит из четырех глав.
ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ В первой главе даются основные определения и термины, ключевые понятия, используемые в диссертации. Разрабатывается аппарат линейных и аффинных преобразований для бинарных диаграмм решений. Проводится анализ существующих направлений работ по данной тематике, а также рассматриваются различные модели представления булевых функций в виде графов.
Аффинное преобразование в матричном виде записывается как: Y = AX + Bt
где матрица А, задающая линейное преобразование, является
невырожденной, то есть:
При этом преобразование затрагивает только входящие переменные.
Если исходная функция была /, то формула f(Y) = A(f(X)) будет
задавать измененную функцию.
Для реальной практической ценности этого метода сокращения размера БДР в результате сложность представления измененной функции и матрицы преобразования должны быть меньше сложности представления исходной функции. Смысл применения линейных преобразований заключается в поиске наименьшей или приемлемой по размеру (в смысле количества узлов) бинарной диаграммы решений преобразованной функции по сравнению с исходной Б/Ц*.
Во второй главе рассматриваются линейные и аффинные преобразования над входящими переменными в контексте сокращения размера БДР, обосновывается оптимальность использования в разработке алгоритмов преобразований над соседними переменными. Предлагается и обосновывается использование аффинных преобразований как расширение линейных преобразований. Обосновывается методология разработки алгоритмов.
Проблема использования алгоритмов с различными переборами заключается в огромном количестве вариантов преобразований.
Всего линейных преобразований от п переменных возможно J|(2" -2'),
i=0 я-1
а количество аффинных 2''-||(2я-2'). Эти числа очень велики, и
1=0
поэтому, даже при существующих мощностях компьютеров перебором
можно решить проблему минимизации только до 6 переменных включительно.
Рассмотрим разложение Шеннона функции по двум переменным:
/ =XiXj2JXi=OXj=0 V */*у/^=0,^=1 VXiXjJxt=l,Xj=0 VXiXjJxt=\>x/=\'
В формуле используются значения четырех подфункций. Число возможных перестановок этих значений: 4!= 24. Рассмотрим число возможных аффинных преобразований над двумя элементами:
V -П(2Л -2і) =4(4-1)(4-2)=24
»=о
То есть получаем, что количество перестановок функций в разложении по двум переменным совпадает с количеством аффинных преобразований над двумя переменными. Для п>2 это количество перестановок кофункций уже не совпадает с количеством аффинных преобразований.
Далее описываются в виде матриц эти преобразования. Для обоснования использования только соседних переменных формулируются и доказываются теоремы — соответственно для случаев линейного и аффинного преобразований. Теорема 2.1. Произведением матриц В, можно получить матрицу
линейного преобразования А для задания любого невырожденного линейного преобразования.
Теорема 2.2. Произведением матриц В~и Dt можно получить матрицу
аффинного преобразования А~..
Показывается возможность сокращения размера бинарной диаграммы решений с помощью аффинных преобразований, заданных расширенной матрицей.
В результате исследования установлено влияние различных базовых преобразований на подфункции и определена зависимость. Как следствие,
стало возможным работать напрямую с бинарными деревьями, на
основании определенных правил, а все изменения воспроизводятся в виде
4 линейных и аффинных преобразований с помощью постепенного
доумножения на матрицы В~и Di.
В третьей главе разрабатываются идеи для построения алгоритмов,
строятся различные алгоритмы и критерии. Вводится определение веса и
однородности. Приводятся описания алгоритмов, которые используют на
каждом шаге только преобразования с соседними переменными:
4 А1 — работающий с разностями весов в поддеревьях.
А2 - сокращающий БДР используя в качестве критерия размер БДР.
A3 - использующий симметрию.
А4 - минимизирующий значение однородности.
В четвертой главе производятся оценки числа шагов алгоритма
однородности, и доказывается теорема о верхней оценке числа шагов
** алгоритма.
Доказаны следующие теоремы:
Теорема 4.1. Значение однородности некоторого уровня L не может
измениться при преобразованиях другого уровня.
Теорема 4.2. S <, Н <, {п -1)2"
Число шагов алгоритма однородности, М:
М = 0(N\ogN), где N = 2".
Теоремы 4.1 и 4.2 позволили обосновать конечность числа шагов
алгоритма однородности и получить верхнюю оценку числа шагов.
В заключении подводятся итоги проделанной работы и делаются выводы.
В приложении приведены исходные тесты разработанного комплекса
** программных средств.
Модели компактного представления бинарного дерева - виды диаграмм
Для компактного представления булевых функций в виде графов, полученных из бинарного дерева, используются различные модели. Далее будут рассмотрены наиболее распространенные из них. Рассмотрим булевы функции, / : В" = В, зависящие от переменных хх,...,хп. Диаграммы решений представляются в виде графа, где каждая не оконечная вершина обозначается переменной x.,l i n. Две исходящие из нее ветви означают декомпозицию функции на две подфункции. При этом граф является направленным и упорядоченным, то есть порядок переменных сохраняется в любом из путей от начала к конечной вершине. Для задания бинарного дерева используются три возможных декомпозиции функции:
При этом /Д,=Д.,Ф/И Здесь / - это значение функции в узле. Бинарное дерево решений строится следующим образом: сначала в корне дерева выполняется соответствующее разложение функции по первой переменной, получаются две подфункции, не зависящие от этой переменной. После этого выполняется разложение по этим двум подфункциям по следующей переменной и т.д. Рекурсия останавливается, когда достигаются оконечные узлы, задающие значение функции для данного маршрута (соответствующего набору значений переменных по которым выполнялось разложение) и принимающие значение 0 или 1, которые и являются значениями функции для данного набора (рисунок 1.1). Рассмотрим булеву функцию f. В" = В от переменных х1,...,х„. Построим для нее бинарное дерево решений, где каждая не оконечная вершина обозначается переменной х,, а две исходящие из нее ветви означают декомпозицию функции на две кофункции Рассмотрим варианты удаления избыточностей для сокращения размера бинарной диаграммы: Тип I: Отождествление изоморфных узлов. Это сокращение узла, если существует другой узел, обозначенный аналогичной переменной, изоморфный этому узлу. При этом вход сокращенного узла перенаправляется на вход узла, которому он был изоморфен (рисунок 1.7).
Тип S: Сокращение вырожденного узла, оба выхода которого указывают на один и тот же узел. Вход сокращенного узла перенаправляется на вход узла, на который указывали его выходы (рисунок 1.5). Тип D: Сокращение узла, у которого единичный выход указывает на О, вход сокращаемого узла присоединяется к узлу, к которому был присоединен нулевой выход (рисунок 1.6). Сокращение типа I или отождествление изоморфных узлов применяется для всех видов сокращений бинарных диаграмм. Типы S и D являются взаимоисключающими.
Линейные и аффинные преобразования переменных и сокращение размера бинарных диаграмм решений
Линейное преобразование переменных означает, что переменная заменяется некоторой суммой по модулю два всех переменных, причем некоторые переменные могут не входить в рассматриваемую сумму. Пусть преобразованных переменных, а = некоторый двоичный вектор. Тогда линейное преобразование переменных задается зависимостью Y = TX, а аффинное преобразование задается выражением Y = TX@D для некоторой невырожденной матрицы Т, все операции выполняются над полем GF(2). Матрица Т определяет способ линейного преобразования. Невырожденность матрицы Т означает, что можно однозначно восстановить исходный входной вектор X, зная вектор Y. Единичное значение координаты вектора D означает, что на соответствующую преобразованную переменную навешивается отрицание. Аффинное преобразование можно свести к линейному, если ввести в столбец переменных дополнительный единичный разряд и произвести окаймление матрицы преобразования: х2 подается х, Ф х2, на третий вход подается х,, на четвертый - х, Ф х2 Ф х4. Линейные преобразования могут привести с существенному сокращению числа узлов в ДР. Пример 2.2 Рассмотрим булеву функцию, заданную вектором: На рисунке 2.1 показана БДР, соответствующая этой функции. Эта БДР содержит 7 узлов. Применим к этой БДР аффинное преобразование из примера 2.1. Бинарная диаграмма решений, соответствующая преобразованной функции, показана на рисунке 2.2.
Рассмотрим невырожденные линейные и аффинные преобразования над соседними переменными. Пусть матрица А - матрица линейного преобразования переменных. Она имеет размер пхп. Так как преобразования являются невырожденными, то матрица А является невырожденной. Отсюда следует, что существует обратное преобразование. Отметим также, что у невырожденной матрицы никакую из строк нельзя получить суммой других строк. Рассмотрим преобразованный вектор ]Га,х,, где at = {0,l}. і Рассмотрим теперь линейные преобразования, получаемые с помощью матрицы, описывающей линейное преобразование над соседними переменными. Эта матрица имеет вид: Формула 2.2 Матрица В, должна быть невырожденной. Эта матрица может описывать одно из следующих преобразований: 1. Замена xt =х,+ xj+l; хм = хм 2. Замена х, =х,; хм = хм + х( 3. Перестановка х, = х1+1; хм = х, В случае аффинного преобразования, псевдопеременную 1 нельзя заменять на сумму и переставлять местами с другими переменными. Поэтому в случае построения матрицы для аффинного преобразования матрица В имеет следующий вид: Формула 2.5 Для реализации аффинного преобразования, совместно с В применяется матрица Д, которая имеет следующий вид: Формула 2. справа располагается в строке /. При умножении на эту матрицу происходит отрицание переменной с номером і. Теорема 2.1.
Произведением матриц В, (Формула 2.2) можно получить матрицу линейного преобразования А. Доказательство Так как матрица А невырожденная, то для доказательства этого утверждения рассмотрим обратный процесс: Из матрицы А произведениями на невырожденные Bt получить единичную матрицу. Рассмотрим матрицу А: Матрица А задает преобразования над исходными переменными. Методом исключения Гаусса для нахождения обратной матрицы преобразовываем А к единичной матрице /, получая А \ при этом каждый из шагов задается в виде произведения матриц В,, так как работа производится на каждом шаге над двумя переменными. Если эти переменные не являются соседними, то сначала производится серия перестановок соседних переменных, чтобы преобразуемые переменные стали соседними, потом выполняется требуемое преобразование и в заключение перестановками возврат в исходное состояние.
Метод двухуровнего перебора (А2)
Выявляем симметрию в /0, /,, f2, /3: если есть пара равных значений, то перестановками приводим к виду: XXYY или XXYZ или YZXX. Если получились 2 пары (случай (XXYY )) , то фиксируем первый уровень, установив 5 = 1. Это означает, что первый уровень больше не преобразовывается. 2) L = L+l,K = 2K. Аналогично рассматриваем подмножества поэлементно равные подмножества, перестановками подмножеств приходим к виду: XXYY или XXYZ или YZXX. Если получились 2 пары (случай (XXYY )), то: Если SZL-1 то возвращаемся на уровень назад. Иначе фиксируем первые уровни, установив S = L. Иначе: если пришлось переставлять подмножества, то возвращаемся на уровень назад. 3) Цикл заканчивается, если L равно количеству уровней в дереве, иначе возвращаемся к пункту 2. Идея этого алгоритма заключается в выявлении случаев симметрии и «поднятии» ее на более высокие уровни, где бы она оставалась в неизменном состоянии, так как симметрия является самым оптимальным вариантом для сокращения числа узлов в двоичном дереве. У приведенных алгоритмов сложно оценить число шагов. Поэтому возникли новые идеи для построения более прозрачного алгоритма, который бы на каждом уровне работы минимизировал бы общий критерий. Это сразу позволит утверждать об отсутствии бесконечных циклов в работе программы, так как на каждом этапе производится улучшение общего критерия, при этом отсутствует влияние на те его составляющие, которые не затронуты на данном уровне. Определение Однородностью Я функции назовем модуль разницы количества единиц и нулей в значении функции: Я = количество элементов 1 - количество элементов 0 . Рассмотрим задание функции в виде двоичного набора длины JV = 2".
Пусть количество единиц в наборе равно Nlt а количество нулевых элементов в наборе равно N0, N = N{ +N0, тогда Я = ЛГ,-ЛГ0 = ЛГ-2ЛГ0. Однородность уровня L будет выражена формулой: На базе введенных определений вводится новый критерий для алгоритма максимизация однородности функции: перестановка прошла успешно (максимизируемое значение изменилось), то возвращаемся на уровень назад. 3) Цикл заканчивается, если L равно количеству уровней в дереве, иначе возвращаемся к пункту 2.
Новый подход позволил предельно упростить критерии, при этом были получены новые результаты. Кроме того, появилась возможность теоретически получить верхнюю оценку сложности работы алгоритма. В главе 3 предложены и разработаны алгоритмы для сокращения размера БДР, которые имеют меньшую сложность и базируются на иных принципах, чем уже существующие. А именно, вместо ограничения переборов, используются критерии, оперирующие с весами подфункций, которые на каждом из этапов выполняют преобразования только над соседними переменными. Для этого были введены необходимые определения и построены критерии. Необходимо определить максимальное количество шагов, которые требуются для остановки алгоритма. Известно, что в силу выбранного критерия, на одном уровне подряд можно сделать не более одной успешной перестановки, удовлетворяющей наложенным ограничениям. Кроме того, особенностью алгоритма является последовательность его работы. На каждом уровне получаются два исхода: успешное преобразование и неуспешное (то есть не было найдено преобразований, которые могли бы улучшить рассматриваемый критерий). В силу строения дерева и применения преобразований только над соседними переменными, при текущих перестановках затрагивается только предыдущий уровень. Это объясняется тем, что преобразования над соседними переменными, соответствующими данному уровню дерева осуществляют синхронные перестановки элементов уровня, разбитых на четверки. А в силу строения бинарного дерева, четверке элементов текущего уровня соответствует пара элементов предыдущего и уже один только элемент еще более верхнего уровня. Отсюда следует, что перестановка элементов в четверке может повлиять только на предыдущий уровень. Пусть S - число успешных преобразований. Количество неудачных попыток не может превышать количество успешных попыток плюс количество уровней в дереве. При этом на первом уровне (преобразования над первой и второй переменной) случаи успеха и неудачи влекут за собой одинаковое действие — спуск вниз, что равносильно неудаче. А каждый случай успешного шага на любом другом из уровней - подъем на один уровень выше. Таким образом, учитывая, что уровней в дереве «-1, получаем число неудачных попыток равно S+w-І, а число шагов алгоритма равно S + S + Мы получили ответ на вопрос, сколько шагов имеют рассмотренные алгоритмы в зависимости от количества успешных преобразований.
Для окончательной оценки необходимо узнать величину S. Теорема 4.1 Значение однородности некоторого уровня L не может измениться при преобразованиях другого уровня. Доказательство Если рассматривать уровень, больший текущего, то будет видно, что преобразования на нем будут находиться внутри блока текущего уровня (рисунок 2.5), так как блок - это пара элементов текущего уровня, которые соответствуют четверке следующего уровня. Поэтому изменения в количестве единиц относительно количества нулей в каждом отдельном блоке не произойдут. Если рассматривать уровень меньший текущего, то получится, что преобразования будут производиться над элементами, каждый из которых является блоком на требуемом уровне. Таким образом, ни в каком из этих случаев не будет изменяться значение однородности текущего уровня, кроме как при преобразованиях над текущим уровнем. Что и требовалось доказать. Из теоремы 1 следует, что с точки зрения критерия однородности все значения однородности различных уровней можно рассматривать отдельно, и алгоритм обеспечивает возможности увеличения значений однородности, производя каждый раз ограниченные манипуляции.
Эффективность работы алгоритмов и их совокупностей на функциях с одним выходом для различного числа входящих переменных
Результаты были получены с помощью собственной программы, написанной на Visual С на компьютере РШ 750MHz. Алгоритмы строились и отрабатывались на всех возможных функциях от количества входящих переменных до 4-х включительно. Это обусловлено размером множества всех вариантов =22". Для тестирования БДР, построенных от 5 и более входящих переменных, применялась генерация 200 случайных тестовых последовательностей из множества {0,1} размером 2" (то есть случайные вектора от п переменных) и брался средний результат процентного сокращения размера бинарных диаграмм. Результаты показаны на рисунках 4.1 и 4.2. На рисунке 4.1 представлены результаты работы описанных выше алгоритмов. Метод частичного перебора с использованием только соседних переменных (алгоритм А2) имеет наилучшие показатели процентного сокращения размера бинарной диаграммы, но рисунок 4.2 демонстрирует, что описанные алгоритмы при совместном использовании дополняют друг друга, улучшая результат при общем высоком быстродействии (на обработку всех 65536 функций от 4-х переменных затрачивается около 1 минуты). К сожалению, при росте количества переменных результаты уменьшения размера бинарных диаграмм от случайной функции в процентном отношении ухудшаются. Это можно легко объяснить. Преобразования ведутся синхронно на четверках элементов. На малых уровнях в каждой из четверок становится очень много элементов, и они стохастически друг друга уравновешивают. На больших уровнях возникает аналогичная проблема, но уже за счет большого количества синхронно преобразуемых четверок. Поэтому необходим более сложный критерий, компенсирующий эти явления, отработанный для функций от большого количества переменных.
Кроме тестов на случайных функциях были произведены тесты на функциях из LGSynth 93. Результаты показаны в таблице. Следует отметить, что для функций с несколькими выходами результаты обрабатывались как несколько функций с одним выходом.. Результаты представлены в двух видах. Сначала сложность функции определяется как сумма сложностей всех диаграмм функций, представляющих ее выходы, а потом с учетом изоморфности, то есть где общие части диаграмм сокращаются и имеют ссылки друг на друга, аналогично сокращениям диаграмм типа I. Функции XOR от большего количества переменных также успешно преобразуются как и XOR5. Результаты приведены для алгоритма А1А2. Результаты алгоритма А4А2 показаны в скобках.
На рисунке 4.2 показаны результаты композиции различных алгоритмов. Результаты продемонстрировали улучшение показателя сокращения размера по сравнению с отдельно взятыми алгоритмами. Но они также показали, что критерии, отработанные на небольшом размере таблицы истинности, не подходят для функций зависящих от 6 переменных и более. Это можно легко объяснить. Преобразования ведутся синхронно на четверках элементов. Получается, что на малых уровнях в каждой из четверок становится очень много элементов, и они стохастически друг друга уравновешивают. На низких уровнях возникает аналогичная проблема, но уже за счет большого количества синхронно преобразуемых четверок. В принципе, это может частично решаться с помощью преобразования, описанного в пункте 2.1 (Линейное преобразование тща. хк=хк_2хк_1г хк_2=хк_2,хк_1=хк_1), но это требует существенного пересмотра логики алгоритмов, а также анализа и поиска характерных случаев при работе с большой размерностью переменных и эти исследования могут быть продолжены в дальнейшем.
Для представления функций с несколькими выходами используется совокупность диаграмм, каждая из которых представляет собой обычную булеву функцию с одним выходом. При этом возможны различные варианты их взаимодействия.
Самым простым был подход рассмотрения нескольких отдельно взятых булевых функций без учета того, что они представляют одну сложную. Под сложностью диаграммы подразумевается сумма сложностей диаграмм, представляющих булевы функции. Этот подход дал возможность тестировать алгоритмы на различных тестовых функциях, признанных как benchmark (LG Synth 93), но у него есть минусы. Для реального представления в виде одной большой схемы общие части схем, реализующих различные выходы, пересекаются между собой.
Следовательно, описанный подход не совсем корректен. Более корректным является подход, где общие части диаграмм сокращаются и имеют ссылки друг на друга, аналогично сокращениям диаграмм типа I. Поэтому он также был опробован, и были получены результаты отличные от первого. Казалось бы, как может уменьшиться количество узлов в совокупности? Ответ на этот вопрос дает приведение функции по принципу сортировки значений. Если после критерия, влияющего на однородность функции, применить критерий, который уточняет его, расставляя элементы функции без нарушения однородности, то становится ясно, что получится сразу два интересных уточнения: 1. Сократится получаемое полученное после применения алгоритмов. 2. В рассматриваемом случае увеличится количество одинаковых блоков булевых функций, которые можно будет сократить преобразованием типа I, примененным между диаграммами, реализующими различные выходы функций.