Содержание к диссертации
Введение
Глава 1. Анализ существующих методов оценки риска 12
1. Методики оценки риска в бизнесе 12
2. Методики оценки риска в технических системах 31
3. Методы оптимизации для многоэкстремальных и многопараметрических функций .36
4. Описание объектов таблицей "объект-признаки" 47
5. Цели и задачи работы .48
Глава 2. Разработка методики логико-вероятностной (лв) оценки риска с учетом групп несовместных событий (ГНС) 52
1. Основные определения теории ЛВ-оценки риска 52
2. Постановка комплексной задачи оценки риска : 53
3. Методика ЛВ-оценки риска с учетом ГНС 57
4. Примеры ЛВ-моделей риска с ГНС 63
5. Анализ индивидуального и среднего рисков 65
6. Выводы 67
Глава 3. Разработка методов идентификации в-моделей риска по статистическим данным 69
1. Постановка задачи идентификации В-модели риска
2. Алгоритм оптимизации 73
3. Метод случайного поиска 76
4. Метод малых приращений 76
5. Метод случайного поиска без учета ГНС 79
6. Оценка временной сложности алгоритма оптимизации 80
7. Иллюстрации по идентификации В-моделей риска 84
8. Идентификация В-модели риска методом анализа причин неуспеха 89
9. Выводы 90
Глава 4. Исследования по идентификации в-моделей риска 92
1. Выбор значений допустимого и среднего рисков 92
2. Определение глобального экстремума и выход из тупиков 93
3. Управление точностью и скоростью обучения 95
4. Задание начальных условий и учет отсутствующих градаций 101
5. Точность оценок вероятностей Pjr и параметров Pm, Pad, dPc 104
6. Обучение и контроль В-модели риска 106
7. Оценка точности и стабильности классификации объектов 117
8. Выводы 119
Глава 5. ЛВ-модели риска в прикладных областях 121
1. Л В-модели кредитного риска физических лиц 121
2. Л В-модели кредитного риска юридических лиц 124
3. Анализ кредитной деятельности банка 130
4. Л В-модели риска мошенничества в бизнесе 138
5. Исследование Л В-моделей риска в бизнесе 147
6. ЛВ-модели риска в структурно-сложных технических системах 151
7. ЛВ-модели риска потери качества 157
8. Выводы 166
Заключение 168
Литература
- Методы оптимизации для многоэкстремальных и многопараметрических функций
- Примеры ЛВ-моделей риска с ГНС
- Метод малых приращений
- Точность оценок вероятностей Pjr и параметров Pm, Pad, dPc
Введение к работе
Настоящее исследование посвящено разработке и исследованию тогико-вероятностных (ЛВ) моделей риска (вероятности) неуспеха в эизнесе и методов их идентификации с учетом групп несовместных юбытий (ГНС).
Актуальность темы. Существуют целые отрасли управления зиском с многочисленными институтами, компаниями и ассоциациями, :пециализируюшимися на задачах измерения и управления риском, іапример Институт по Управлению Риском (IRM), Ассоциация Ірофессионалов Риска (GARP) и др.
Имеется несколько подходов к решению задач риска в бизнесе и :ачестве. Одни из них основаны на экспертных оценках и на системе ейтингов. В других методах оценка риска рассматривается как задача лассификации и используются методы дискриминантного анализа и :ейронные сети. Эти методы не позволяют вычислить риск объекта как ероятность неуспеха (неблагоприятного события).
Возникла необходимость создания новой методики комплексной исленной оценки риска неуспеха, которая демонстрировала бы сущест-енно большую точность и стабильность в классификации объектов и ешала бы также задачи численной оценки и анализа риска, определения ены за риск и управления риском.
В работах научной школы И.А. Рябинина создан эффективный тпарат ЛВ-моделирования риска в технических системах. Однако в ;хнике не решен ряд задач для бизнеса и банков: 1) события зссматриваются только на двух уровнях, в то время как в бизнесе и інках события имеют число уровней от 2 до 10 и нужно вводить ГНС; і задача идентификации ЛВ-моделей риска по статистическим данным шее не решалась, так как катастрофы и аварии единичны и при оценке их іска считают известными вероятности отказов элементов системы; структурная и логическая модели риска эквивалентны реальной схеме, тример электрической, однако в банках и бизнесе модели риска ляются ассоциативными, построенными на здравом смысле связи бытии при неуспехе и могут рассматриваться только как гипотезы.
Отсутствие методов идентификации ЛВ-моделей риска по статис-ческим данным препятствует применению таких моделей для оценки іска в областях, где риск носит массовый и обычный характер и имеются ютоколы данных об успехе или неуспехе каждого объекта. К таким об-стям относятся: банки, бизнес, управление качеством, страхование и др.
Цель работы заключается в разработке и исследовании логико-роятностных моделей риска.(вероятности) неуспеха в бизнесе с учетом 1С и методов идентификации ЛВ-ыоделей риска неуспеха по статисти-жнм данным.
Для реализации поставленной цели в работе решаются следующие задачи:
-
Анализ существующих методов оценки риска в экономике і технике и методов идентификации моделей с большим числом параметров:
-
Постановка комплексной задачи риска;
-
Разработка методики для ЛВ-оценки и анализа риска неуспеха учетом ГНС:
-
Разработка и исследование методик идентификации ЛВ-моделеі риска неуспеха по статистическим данным:
5. Апробация предложенных методик для оценки и анализа риск,
для систем разной логической сложности и в разных предметных областя:
с использованием созданных программных средств.
Методы исследования. Исследования проводились с использова нием логико-вероятностной теории, методов искусственного интеллекта вычислительной математики, исследования операций, адаптивного управ ления, алгоритмов классификации и распознавания образов. Основны! методом исследования являлся вычислительный эксперимент на персональ ных ЭВМ типа IBM PC и сопоставление точности разных методик пр: использовании одних и тех же статистических данных. Комплекс програм мных средств, реализующих методики, разработан в среде Borland C++ 3. для MS-DOS и в Visual C++5.0 и DELPHI 4.0 для WINDO WS 95.
Научная новизна исследования заключается в решении новых зада моделирования и анализа риска в новых предметных областях риска н основе логико-вероятностного подхода. Впервые решены следующи задачи:
-
Сформулирована комплексная задача риска неуспеха, включак щая в себя численную ЛВ-оценку риска (вероятности) неуспеха, классифк кацию объекта по риску, анализ индивидуального и среднего рисков назначение цены за риск.
-
Разработана методика ЛВ-оценки и анализа риска неуспеха учетом ГНС.
-
Разработаны методики идентификации вероятностных моделе (В-моделей) риска с учетом ГНС и выполнены соответствующие расчетны исследования.
Практическая ценность. Разработанные методики позволяю решать следующие практически важные задачи:
-
Вычислять риск неуспеха объекта, сравнивать его риск с средним и допустимым риском, рисками других- объектов, обосноваун назначать цену за риск, анализировать вклады в риск объект инициирующих событий.
-
Осуществлять анализ совокупноцти объектов или их состояли по риску с оценкой вкладов признаков и градаций з средний риск и те; самым управлять риском.
3. Существенно увеличить точность и стабильность классификации объектов по сравнению с западными методиками.
Реализация и внедрение. Научные результаты работы и программы внедрены:
- в АКБ "Петровский" создан тренажер для обучения сотрудников принятию решений по кредитным рискам;
- в учебном процессе и лабораторных работах студентов СГУАП.
Апробация работы. Результаты диссертации докладывались на: конференции "Региональная информатика- 96", СПб., СПИИ РАН; Межд. конф. "Приборостроение в экологии и безопасности человека", СПб., ISA, 1996, 1998; Школе "Фундаментальные и прикладные проблемы теории точности и качества машин, приборов и систем", 1998, СПб., ИПМАШ РАН; Международном конгрессе ICSC "Computational intelligence: method and applications (CIMA'99), Rochester Institute of Technology, RIT, Rochester, N.Y., USA, 1999, June; 2-ой Межд. конф. по проблеме логико-лингвистического управления динамическими объектами, СПб., ИПМАШ РАН, июнь, 1999; Межд. конф. по адаптивному управлению, С-Петербургский Гос. Университет.сентябрь, 1999.
Публикации. Результаты работы отражены в 2 книгах и 6 статьях.
Структура и объем работы. Диссертация состоит из введения, пяти глав, заключения и списка литературы. Общий объем работы t?страниц с ад рисунками, .&Q. таблицами и списком литературы из &3наименований.
Методы оптимизации для многоэкстремальных и многопараметрических функций
Объекты риска Т ={ 1,2,...,N} в изложенных выше методиках описываются набором признаков (характеристик) S = {l,2,...,j,...,n}, каждый из которых имеет свой набор градаций Gj = {l,2,...,Nj}, jeS. Объект - это изделие, которое может потерять качество в процессе производства, кредит, который может быть не возвращен, и т.д [54,55].
При описании отдельного объекта каждый признак] принимает одно значение г є Gj. Таким образом объект описывается п градациями (гі,Г2,...,Гп) где г, є Gj и j є S. Признаки - это параметры или характеристики объекта, для измерения которых используются шкалы логическая (истина или ложь, 1 или 0), качественная (синий цвет, красный и т.д.), линейного порядка (аі 3,2 ... ап), числовая (интервалы [a,b], [Ь,с] и др.). Градации - это конкретные значения параметров или характеристик.
Градации не являются линейно упорядоченными и нельзя сказать, что одна градация хуже или лучше другой для итогового события. Итоговый признак также имеет градации. Например, множество возможных состояний технической системы может разделить на следующие состояния (градации, подклассы): 1- система исправна и работоспособна; 2 - система неисправна, но работоспособна; 3 - система неработоспособна, но может быть восстановлена; 4 - система работоспособна, но ее эксплуатация нецелесообразна из-за больших эксплуатационных затрат. Или для кредита имеем следующие градации: 1 - кредит возвращен; 0 - кредит не возвращен.
Набор данных представляют таблицей (табл. 1.1) со строками-объектами Ті, Тг,..., TN. Такой набор данных является моделью для множества объектов или моделью состояний одного объекта. Связи в таблице выражены в неявной форме. Под "объектом" принято понимать каждую строку таблицы, а под "признаком" - столбцы, помеченные именем признака Si, S?,..., Sn. Номер строки таблицы отождествляется с номером "объекта" или экспериментальных (статистических) данных. Тіт2TN 1 Gjr, r=l,Nj Модель данных в виде таблицы "объект-признаки" (табл. 1.1) всегда привлекала внимание исследователей. По сути речь идет об извлечении закономерностей из набора экспериментальных данных. Эта направление рассматривается в разделе "Data Mining" искусственного интеллекта и признается одним из актуальных. Основой классификации объектов в Data Mining является анализ частот признаков и градаций и их логических комбинаций в "плохих" и "хороших" объектах [56,57]. Настоящая работа также посвящена этой проблеме и решает ее ЛВ-методом.
Исходя из вышеизложенного, можно сделать следующие важные выводы:
1. Для работы банков и прочих финансовых институтов характерно большое разнообразие рисков, но риск кредитования является наиболее важным ключевым фактором, определяющим эффективность их деятельности. Следовательно, оценка кредитного риска, определяемого как вероятность невозврата кредита, является главной задачей.
2. Для оценки риска кредитования существует ряд методик, таких как системы рейтингов, статистические методы [58], методы распознавания образов [59,60,61,62,63], искусственного интеллекта [56,57,64,65,66] и нейронных сетей [17,67]. Наилучшие результаты показывает методика на основе нейронных сетей, однако она не может дать оценку риска кредитования как вероятности невозврата кредита, вследствие накладываемых на нее жестких ограничений. В тоже время представляется возможным поставить задачи риска на единой строгой методической основе, а именно с использованием логико-вероятностного метода [2 4,24,68,69].
3. Все имеющиеся методики обладают рядом недостатков [70], а именно: - качественная оценка риска невозврата кредита ( "хороший" кредит или плохой", 0 или 1, величина того, насколько он "плох" или "хорош" не учитывается); - невозможно оценить вклад каждой характеристики кредита в риск; - невозможно установить допустимый риск и обоснованно назначать цену за риск. - невозможно получить однозначную оценку риска; - невозможно учесть результаты статистического анализа случаев невозврата кредитов; - невозможно прогнозировать размер ущерба.
Для эффективной оценки банковских рисков необходимо создать новую методику точной численной оценки риска, которая была бы лишена упомянутых недостатков.
4. Мошенничество является актуальной задачей. В любом финансо вом институте или банке имеется риск мошенничества. О наличии мошен ничества говорят определенные симптомы. Чтобы принять решение о расследовании необходимо оценить риск мошенничества на основании этих симптомов [9]. Западная методика позволяет оценить вероятность мошенничества только качественно. Актуальность задачи выявления мошенничества приводит к необходимости разработки новой эффективной методики количественной оценки риска мошенничества.
5. Объекты риска в бизнесе описываются набором признаков, каждый из которых имеет свой набор градаций. События, связанные с неуспехом объекта вследствие признаков, являются случайными независимыми событиями, а совокупность событий для градаций образует ГНС.
Риск в бизнесе является обычным и массовым явлением и имеются статистические данные по неуспехам объектов за предыдущий период времени.
5. В настоящее время в технике широко используются логико-вероятностные методы (ЛВМ) оценки риска функционирования структурно-сложных систем. ЛВМ позволяют объективно выявлять наиболее опасные места, причины и инициирующие условия. С помощью этой модели удается также вычислить вклад любого инициирующего условия в общий риск системы. К основным достоинствам ЛВМ относится также получение точной численной оценки риска системы, которая выражается как вероятность отказа [2-4,20,21].
Однако для задач оценки риска в бизнесе и банках методы ЛВТ не применялись из-за отсутствия методов идентификации В-моделей по статистическим данным. До настоящего момента не предпринималось никаких попыток создать на основе ЛВТ новую эффективную методику численной оценки банковских рисков и мошенничеств в бизнесе. В областях экономики, непосредственно связанных с риском, теория логико-вероятностного моделирования не известна.
Примеры ЛВ-моделей риска с ГНС
В главе изложены результаты исследований по идентификации В-моделей риска, приведены приемы по выбору значений допустимого и среднего рисков, определению глобального экстремума и выхода из тупиков, изложено управление точностью и скоростью обучения, задание начальных условий и учет отсутствующих градаций, приведены результаты по обучению и контролю В-модели риска, точности и стабильности классификации объектов. Исследования по идентификации В-моделей риска выполнены с помощью созданного программного комплекса, позволяющего проводить анализ кредитного риска для физического лица и обучать соответствующую В-модель по статистическим данным.
При идентификации В-модели необходимо решить задачи определения расчетного числа хороших объектов Ngc; выбора значения среднего риска РаУи значения допустимого риска Pad.
Цена ошибок при классификации хорошего и плохого объектов разная. Отношение этих ошибок (3.3) считается заданным. В случае кредитных рисков его значение равно Egb=2-M-. Нужное значение Ngc определяют после выполнения нескольких расчетов при разных Ngc по величине Е8ь (рис.4.1,а). При этом наряду с Ngc, получаем также значения допустимого риска Pad и характеристику распределения рисков dPc.
Из таблицы известно среднее статистическое значение риска Pav. В процессе обучения В-модели риска получают среднее расчетное значерше риска РІШ. Возникают вопросы, при каком среднем значении риска Pz обучать В-модель риска и как влияет величина Pz на значение целевой функции Fmax. Результаты идентификации В-модели риска при разных значениях Р7, приведенные на рис. 4.1 ,Ь позволяют сделать ряд выводов: 1) максимальное значение целевой функции Fmax не зависит от величины Pz; то есть задача оптимизации имеет много решений с максимальным значением г 2) при разных Pz, естественно, получаем другие значения вероятностей Pjr, допустимого риска Pad и характеристики распределения рисков объектов dPc; 3) вероятностный смысл В-модель риска получает при Pz = P,m 4- Pav, так как в этом случае все результаты согласуются со средним риском по реальным данным. 2. Определение глобального экстремума и выход из тупиков
В зависимости от параметров kl, k2, k3 формулы обучения (ЗЛО) при выбранных Ngc и Р7 получают разные значения целевой функции Fmax (разные локальные экстремумы). Решение в каждом локальном эксгремуме можно характеризовать как Fmax, Pjr, }=\,Щ r=l,Nj, так и разностью максимального и минимального риска объектов dPc Pi max - Pi min в таблице "объект-признаки". Строится ступенчатая зависимость функции Fmax от параметра dPc (рис.4.1,с), позволяющая определить глобальный экстремум. Изменяя параметры kl, k2, кЗ, определяющие интенсивность обучения, можно получить оптимальное значение dPc и соответственно максимальное значение Fmax.
В процессе обучения ЛВ-модели встречаются тупики, когда в цикле из Nmc попыток поиска оптимальных Pljr не произошло ни одного
Зависимости для целевой функции оптимизации: а - выбор расчетного числа хороших кредитов; b - задание среднего риска; с - определение глобального экстремума. улучшения целевой функции Fmax. Для методов оптимизации на основе случайного поиска (ЗЛО) и малых приращений (3.11) предложены способы выхода из тупиков. Например, в методе случайного поиска для выхода из тупика используется выражение (3.9).
Управление процессом обучения осуществляется в режиме диалога. Необходимость управления возникает при идентификации новой модели риска и для существенного ускорения счета.
Экран дисплея разделен на три окна (рис. 4.2). Первое окно содержит название параметров и поля ввода их значений. Во второе окно выводятся основные параметры результатов счета, позволяющие судить о процессе оптимизации. Третье окно задает клавиши, чтобы остановить программу для изменения параметров (F1), запустить программу после изменения параметров (F2), выйти из программы (ESC).
На рис. 4.2 используются следующие обозначения параметров: kl - коэффициент скорости обучения в формулах (3.10) или (3.11) в зависимости от метода обучения; к2 - модуль наибольшей величины случайных чисел при оптимизации методом случайного поиска; кЗ - величина малого приращения вероятностей в формуле (3.15); к4 - коэффициент формулы для выбора начального приближения при поиске допустимого риска: Pad=Pim+k4 dP, (4.1) Управление обучением JIB - модели риска с экрана дисплея кб - число последних циклов оптимизации, для которых заданы постоянные dPjr, dPljr; k7 - номер оптимизации, с которого результаты записываются в файл; Pav - средний риск по таблице "объект-признаки"; Nmc - число попыток Монте-Карло в методе случайного поиска для улучшения целевой функции в одном цикле оптимизации; Ngc - заданное расчетное число хороших объектов; Nopt - заданное число оптимизаций для процесса поиска максимального значения целевой функции. Состояние и динамика обучения выводятся на экран (рис.4.2,окно 3). Поясним только параметры, которые не были описаны ранее: Ncurmc - текущий номер попытки оптимизации в цикле из Nmc попыток; №Ргтс - номер попытки, в которой произошла оптимизация в предыдущем цикле и получены результаты, приведенные в окне 3; dPc, dP - характеристики распределения рисков объектов; в формулы (4.2), (4.4) подставляются за предыдущий цикл.
Время обучения. Время идентификации рассмотрим на примере идентификации В-модели кредитного риска. Оно зависит от ряда параметров: 1) Числа попыток оптимизации Nmc методом случайного поиска в одном цикле. Задавалось равным Nmc=250r300. В начале оптимизация идет за счет случайного поиска, а далее часто встречаются "тупики". После отступления (3.8) от достигнутого Fmax лучшее решение находится уже за 1-30 попыток и можно уменьшить ЧИСЛО Nmc 2) Числа оптимизаций Nopt. Значение целевой функции в основном увеличивается на 2 и ее начальное значение задается равным Fmax=N/2. Тогда число оптимизаций следует задать Nopt=N/4. В начале процесса оптимизации целевая функция увеличивается на 2т20 единиц. Некоторая избыточность Nopt нужна из-за большого числа "тупиков". 3) Времени поиска допустимого риска Pad = Pad + dPad. В качестве ПерВОГО Приближения ИСПОЛЬЗуеТСЯ Pad = Pim + lu dP, ГДЄ dP=Pad - Pim В предыдущем цикле оптимизации. Коэффициент к.4 в процессе оптимизации можно увеличивать от 0 до 0.9 и тем самым существенно увеличить скорость вычислений.
Метод малых приращений
О мошенничестве со стороны руководителей свидетельствуют особые симптомы. Описанию этих симптомов были специально посвящены некоторые публикации отдельных специалистов и Ассоциации дипломированных бухгалтеров (СРА). При оценке степени риска в отношениях с клиентом метод симптомов стал в последнее время обычным в деятельности аудиторов [ 9 ].
Для того чтобы эффективно выявлять мошенничество необходимо разработать его структурную модель, то есть "дерево событий". О вероятности конечного события - мошенничества со стороны менеджера фирмы - можно говорить при наличии соответствующих симптомов или признаков. Несмотря на существование в литературе огромного количества различных признаков мошенничества со стороны менеджеров, все они разделяются на четыре основных категории: 1. Аномалии в деятельности предприятия; 2. Личные качества менеджеров, свидетельствующие о наличии у них возможных мотивов; 3. Аномалии в организационной структуре фирмы; 4. Особые отношения со сторонними партнерами. В свою очередь эти группы включают в себя другие настораживающие моменты и причины, которые приводят к появлению данных признаков мошенничества. Таким образом эти причины "более низкого уровня" будут инициирующими событиями для основных признаков, а основные признаки будут производными от них событиями.
Например, для признаков первой категории инициирующими событиями будут признаки мошенничества в финансовой отчетности и других документах предприятия; для признаков второй категории - качества менеджера, которые могут стать сигналом о его нечестности; для третьей категории - непонятные на первый взгляд или не имеющие под собой законного основания организационные особенности фирмы; для четвертой категории - создание таких отношений с партнерами по бизнесу, которые способствуют совершению мошенничества или помогли бы его скрыть.
Поскольку наличие определенных симптомов не является доказательством совершения преступления, то соответствующие им инициирующие события имеют определенную вероятность и являются случайными совместными и независимыми событиями.
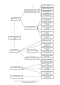
В соответствии с вышеизложенным и исходя из западной методики выявления мошенничества [ 9 ], предлагается следующая структурная модель мошенничества со стороны менеджера, представленная на рис. 5.3.
На схеме номерами 53 - 93 задаются инициирующие события, а номерам 94 - 103 соответствуют производные. Ниже приведены описания событий: вероятность мошенничества со стороны менеджеров. 99 - вероятность мошенничества в связи с личными качествами менеджеров, свидетельствующими о наличии у них возможных мотивов.
События 53-58 инициируют мошенничество в связи с наличием личных долгов или финансовых запросов; пристрастием к азартным играм и рискованным сделкам; неясным или уголовным прошлым; зависимостью финансового благополучия только от деятельности данной фирмы; нечестным или неэтичным поведением на работе. - вероятность мошенничества вследствие аномалий в организационной структуре фирмы.
События с номерами 59-64 инициируют мошенничество вследствие наличия излишне усложненной организационной структуры; отсутствия эффективно работающего подразделения внутрифирменного аудита; отрасли, связанной с высоким риском и приверженности к высокорискованным операциям; использования устаревших или изношенных средств производства; частых изменений в рядах высшего звена управления и директоров; крупных сделок с родственными партнерами. -вероятность мошенничества из-за аномалий в деятельности фирмы. События 65-75 инициируют мошенничество из-за необъяснимых изменений в балансовой отчетности; работы на грани кризиса; необходимости показывать в отчете высокую доходность; необычных или крупных выгодных сделок в конце отчетного периода; ухудшения качества прибыли; недостаточности основного капитала; высокой задолженности или большого удельного веса накладных расходов; трудностей во взимании дебиторской задолженности и проблем, связанных с движением финансовых средств; более быстрого роста расходов по сравнению с доходами; зависимости от производства лишь одного-двух изделий (услуг); участия фирмы в крупных судебных процессах. - вероятность мошенничества в связи с особыми отношениями со сторон ними партнерами.
Точность оценок вероятностей Pjr и параметров Pm, Pad, dPc
В данной структурной модели РПК можно рассмотреть отдельно каждый из двухсторонних зазоров в паре канал-колесо и размеры других деталей, влияющих на состояния Zji, Zji, Zj3. Тогда получится другие Л- и В-модели риска. Однако это не является препятствием для вычисления и анализа риска и обучения модели риска по данным таблицы "объект -признаки".
Пример 2. Рассмотрим еще один пример РПК из-за неточности изготовления деталей. Пусть нашими деталями являются большие разные кубики. РПК всего изделия зависит от суммарного размера В для п деталей, расположенных в линию вплотную друг к другу (рис. 5.10, а). Допуск на размер 1-ой детали dBi = Bi max - Bi min разбит на Ni градаций, допуск на размер 2-ой детали ёВг разбит на N2 градаций, допуск на размер 3-ей детали сШз разбит на Кз градаций и т. д. Число градаций для размера каждой детали составляет, например, от 2 до 11 и число деталей равно п=20. Разное количество возможных сборок является громадным числом порядка 520.
Размеры Bi, В2, ..., Вп измеряются с помощью калибров (скоб), номера которых соответствуют градациям соответствующего размера. Каждый из размеров Bi, В2, ..., Вп невозможно измерить с помощью стандартного штанген-циркуля.
Итоговый размер В = Bi + В2+ ... + Вп можно измерить после сборки, например по расстоянию последней детали до некоторой известной (контрольной) плоскости, и присвоить ему одну из трех градаций: 1 - размер меньше нормы, 2 - размер в норме, 3 - размер больше нормы.
В-модель риска может быть обучена по статистическим данным по многим сборкам. Тогда по значениям градаций деталей Bi, В2,.... Вп можно прогнозировать риск неуспеха каждого нового изделия.
Если имеется возможность для некоторых других промежуточных измерений размеров, например от четырех последовательных деталей, от десяти деталей и т. д. и введены градации для этих измерений, то можно составить несколько Л-функций риска и их комбинаций. Если строится из "кубиков" какое-то изделие не в линию, а на плоскости, то также можно записать несколько Л-функций риска и их комбинаций. Для пространственного расположения "кубиков" (рис.5.10, б) точно также можно записать ЛВ-модели РПК.
Пример 3. Риск потери качества из-за комплектующих. Объект использует п комплектующих (признаки), каждое из которых в период времени Т может отказать. Отказ может быть с одним, двумя, тремя, или всеми комплектующими. События, заключающиеся в отказе комплектующих, будем считать независимыми. РПК объекта будем описывать структурной моделью риска типа "узел", приведенной на рис. 2.1,а и соответствующими Л- и В-моделями риска (2.21), (2.23).
Выполнено обучение модели риска (2.23) для объекта из п=20 комплектующих, каждое из которых имело от 2 до 11 градаций. Всего градаций 94. Обучение выполнено по таблице из 1000 объектов. По каждому объекту известны градации его признаков и итогового события. Средний риск отказа объектов по таблице равен Pav=0.3.
Смысл градаций для модели РПК может быть таким: время установки комплектующего с момента его изготовления. Для каждого комплектующего j=l,n число градаций по величине срока разное. Например, первое комплектующее имеет такие градации: 1 - до 3-х месяцев; 2 - до 6-ти месяцев и т.д. Всего 5 градаций.
Пример 4. Обучение модели риска потери качества для изделия "мостик". Для обучения модели РПК изделия типа "мостик" (рис. 2.1,Ь) использовалась таблица с 1000 объектами и Л-модель риска (2.25), имею-. щая повторные элементы. Объект риска потери качества имеет 5 признаков, которые имеют от 4 до 11 градаций; всего 40 градаций.
Возможная интерпретация для градаций инициирующих и итогового признаков для мостика следующая. Узлы Хі,Х2,Хз,Х4,Х5 изделия "мостик" собирают соответственно бригады Аі,А2,Аз,А4,А5 с числом рабочих (с личным клеймом) равным числу градаций в признаке. Собранные изделия поступают на испытания, которые успешны (градация 1) или неуспешны ( градация 0 ). Протокол испытаний составляется в форме таблицы "объект-признаки". Естественно, вместо рабочих может быть разное технологическое оборудование, станки, фирмы, поставляющие комплектующие.
Среди N=1000 объектов испытания выявили Ng=700 хороших и Nb=300 плохих объектов. По таблице "объект-признаки" и В-модели риска (2.23) нужно определить вероятности Pjr, j=l,n; r=l,Nj, связанные с градациями признаков. В-модель мостика успешно обучена методом случайного поиска с учетом ГНС. Общее число независимых оцениваемых параметров-вероятностей равно Х"=і " ї- Результаты исследований в табл.5.9 - 5.11 позволяют сделать следующие выводы:. 1) Наибольшие вероятности Pjm и вклады в средний риск вносят признаки 1 и 4. 2) Средние вероятности для признаков Pjm отличаются почти в два раза (табл.5.10). Наименьшую вероятность имеет признак 5, имеющий наименьший структурный вес. 3) Относительные частоты градаций Wjr и их вероятности Pljr в ГНС, хотя и составляют каждая в сумме 1, могут существенно отличаться между собой (например, Wjr и PlJr в табл.5.11). Такое сравнение полезно для анализа риска таблицы объектов.