Содержание к диссертации
Введение
1. Линейная оценка прогнозирования и ее динамические свойства 15
1.1. Задача линейного прогнозирования. Синтез адаптивного алгоритма 15
1.2. Анализ динамических свойств. Теоретико-информационный подход 32
1.3. Результаты математического моделирования 39
Выводы 43
2. Проблема случайных импульсных искажений в данных 44
2.1. О влиянии случайных импульсных искажений на точность и динамические свойства линейной оценки прогнозирования 44
2.2. Синтез оптимального алгоритма 56
2.3. Результаты математического моделирования 62
Выводы 69
3. Обнаружение случайных импульсных искажений 70
3.1. Задача обнаружения разладки случайного временного ряда 70
3.2. Синтез алгоритма 74
3.3. Оптимизация порога обнаружения 79
3.4. Результаты математического моделирования 80
Выводы 86
4. Разработка автоматизированной системы прогнозирования и примеры ее практического применения 87
4.1. Разработка программного обеспечения 87
4.2. Разработка автоматизированной системы прогнозирования 90
4.3. Задача прогнозирования динамики рыночной конъюнктуры 101
4.4. Задача селекции движущихся радиолокационных целей на фоне комбинированной помехи 108
4.5. Задача распознавания речевых сигналов при действии импульсных помех 115
4.6. Выводы 122
Заключение 123
Список литературы 126
Приложение 135
- Анализ динамических свойств. Теоретико-информационный подход
- О влиянии случайных импульсных искажений на точность и динамические свойства линейной оценки прогнозирования
- Задача обнаружения разладки случайного временного ряда
- Задача селекции движущихся радиолокационных целей на фоне комбинированной помехи
Введение к работе
Временной ряд - это расположение во времени статистического показателя, отражающего ход развития изучаемого процесса. Временные ряды исследуются с различными целями. Из них можно выделить две основные цели:
определение природы ряда;
прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям).
Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана. Как только модель определена, можно с ее помощью интерпретировать рассматриваемые данные (например, использовать в теории для понимания сезонного изменения цен при анализе социально-экономических процессов). Не обращая внимания на глубину понимания и справедливость теории, можно экстраполировать затем ряд на основе найденной модели, т.е. предсказать его будущие значения.
Исходный временной может представляться суммой случайных и детерминированных компонент, или являться коррелированным случайным процессом. Детерминированная (строго определенная) компонента может состоять из циклических компонент и так называемого тренда. Ярким примером циклической компоненты может служить сезонность - зависимость от времени года. Встречаются также циклы другой длительности, обусловленные появлением новых, а значит исчезновением старых товаров, технологий и научных методов. Тренд есть общее направление развития процесса в рассматриваемом периоде времени и чаще всего это результат постоянного воздействия какого-либо важного фактора. Однако тренд может быть всего лишь частью некоторого цикла с периодом большим, чем рассматриваемый временной отрезок.
Случайная составляющая временного ряда возникает в результате воздействия на исследуемый процесс огромного количества благоприятных и
5 неблагоприятных для данного процесса факторов с различными последствиями,
сроками действия. Применительно к экономическим процессам, например, к
курсовой стоимости акций, можно сказать, что рынок формируется
множеством покупателей и продавцов, каждый из которых преследует свои
цели, - это может быть и спекулятивная игра, и скупка контрольных пакетов
акций, и просто вложение временно свободных средств в надежде на прибыль.
Вдобавок, рынок весьма неоднозначно реагирует на разного рода заявления
политиков, экономистов, различного рода скандалы и слухи.
Однако не всегда удается добиться достаточного качества обработки временного ряда ввиду возможного наличия в исследуемом периоде данных большого количества непредсказуемых событий (помех), особенно в задаче экономического прогнозирования. К непредсказуемым событиям относятся такие, для предвидения которых в момент составления прогноза нет необходимых данных, или такие, природа которых неопределенна. Таким образом, кроме детерминированных и случайных величин бывают ещё и неопределенные [39]. Между тем, математическая модель может содержать либо детерминированные, либо случайные величины.
Непредсказуемые события могут быть двух видов: приводящие к долговременным изменениям статистических характеристик ряда (ступенчатое изменение) (рис. В. 1.6) и кратковременные случайные импульсные отклонения (импульсные помехи) (рис.В.І.а). В первом случае нарушается стационарность случайного процесса и осуществляется скачкообразный переход от одних статистических закономерностей к другим. При этом вся предшествующая выборка оказывается непригодной для последующего использования. Воздействие единичной импульсной помехи (ИП) не приводит к глобальным изменениям статистических характеристик случайного процесса. Однако выборка в данном случае оказывается также непригодной для получения каких-либо приемлемых статистических оценок. В указанном случае могут быть предложены несколько вариантов решения этой проблемы:
a)
б)
Рис. B.l - Возможные состояния временного ряда до и после воздействия непредсказуемых событий (случайное импульсное отклонение (а) и ступенчатое изменение (б)).
- отказ от использования выборки до момента воздействия импульсной
помехи включительно. В этом случае проблема малых выборок обостряется в значительной степени, т.к. имеющегося объема наблюдений для настройки любой модели может оказаться недостаточно;
- устранение пораженного отсчета из выборки. В этом случае возможно
нарушение сезонных циклических составляющих случайного процесса;
- устранение влияния пораженного отсчета путем его восстановления.
Последний вариант является наиболее предпочтительным, т.к. позволяет
сохранить целостность выборочных данных.
Кроме рассмотренных социально-экономических процессов, эти проблемы возникают и при анализе процессов в радиосистемах. Обработка информации на фоне помех на протяжении многих лет является одной из актуальных задач радиотехники. Например, решение задачи защиты от стационарных коррелированных помех может осуществляться с использованием процедур декорреляции (обеления) выборочных данных [44] с использованием устройств автокомпенсации [90]. Т.к. в большинстве случаев вероятностные характеристики случайных процессов и помех неизвестны, или они изменяются во времени, то целесообразно использовать адаптивные алгоритмы декорреляции. Во многих случаях они имеют явные преимущества по сравнению с другими методами статистической обработки данных.
В общем виде структура обеляющего фильтра показана на рис. В.2.а. Ключевым звеном обеляющего фильтра является фильтр линейного предсказания (ФЛП). Его решетчатая реализация показана на рис. В.2.6. При анализе блок-схемы решетчатого ФЛП становится очевидной природа негативного влияния импульсных помех на качество обработки входной последовательности х(п). При прохождении импульсной помехи через ФЛП, она воздействует на него, как минимум, в промежуток времени At=M, где М -количество звеньев в фильтре. В этом случае не происходит полного
As
x(n)
Tj(n)
-aM (X
-aj (X) -a2 (X
x(n -1) x(n - 2)
x(n-M)
Фильтр линейного предсказания
a)
б)
Рис. В.2. - Структурная схема обеляющего фильтра (а) и решетчатая реализация фильтра линейного предсказания (б).
9 «обеления» случайного процесса х(п), и, следовательно, снижается
эффективность подавления комбинированной помехи.
Проблема импульсных помех также актуальна при решении широкого рода задач, а не только задачи прогнозирования временных рядов. Одной из них является задача подавления активных и пассивных помех в системах селекции движущихся целей в РЛС [90]. Любая РЛС подвержена воздействию пассивных помех, представляющих собой отражения от подстилающей поверхности, гидрометеоров (облака, дождь, туман и т.д.) и сосредоточенных местных предметов, как правило, искусственного происхождения (инженерные сооружения, здания, трубы заводов и т.д.). Пассивные помехи в общем случае нестационарны во времени и неоднородны в пространстве, их мощность может намного превышать мощность полезного сигнала.
Также проблема импульсных помех стоит очень остро и в задаче распознавания речевых сигналов. Импульсные искажения здесь возникают в основном в аналоговых и цифровых системах передачи речи и могут иметь различную природу: ненадежная работа системы питания, помехи от системы зажигания в автомобиле и т.п. В этом случае также необходима защита от импульсных помех для обеспечения надежности работы подобных систем.
Однако существует ряд методов, направленных на устранение импульсных помех. Вопросам построения систем, устойчивых к воздействию импульсной помехи, посвящено большое число работ [48, 79 и др.]. Многочисленные алгоритмы можно разделить на три группы [51]. К первой принадлежат способы борьбы, основанные на ограничении сигналов (схемы типа ШОУ, ШОС) или схемы с ключевыми АРУ. Однако, они применимы только к некоторым типам сигналов, приводят к их искажению, существенно уменьшают отношение сигнал/шум.
Ко второй группе принадлежат алгоритмы, основанные на непараметрических методах статистики [48], устойчивые к действию помех. Однако они требуют некоторой обучающей выборки из ансамбля помех, относительно которой формируется решающая статистика. Причем элементы
10 выборки из ансамбля помех должны быть независимыми. Применение таких
методов к типичной задаче обнаружения сигнала с неизвестным временным
положением на интервале, содержащем много элементов разрешения по
задержке на фоне коррелированных шумов, вызывает большие затруднения.
К третьей группе принадлежат адаптивно-компенсационные алгоритмы. Они весьма сложны и работоспособны при очень большом отношении помеха/сигнал, из-за чего резко уменьшаются границы их применения.
Также существует ряд алгоритмов сглаживания импульсных помех. Сглаживание импульсного шума, очевидно, требует обнаружения искаженных элементов сигнала и последующего оценивания их значений по значениям неискаженных элементов. Вообще говоря, алгоритмы сглаживания таких помех должны быть двухпроходовыми с разметкой искаженных элементов на первом проходе и оценкой их сглаженных значений на втором проходе. Но для упрощения можно сделать алгоритм однопроходовым, совместив операции обнаружения и оценивания в одном проходе.
Разметка элементов изображения на искаженные шумом и не искаженные (обнаружение выбросов шума) может быть выполнена на основании проверки гипотезы о принадлежности центрального элемента некоторой локальной окрестности той же выборке, что и заданное большинство остальных элементов окрестности, или выпадения ее из этой выборки. Для решения этой задачи обычно используются алгоритмы, основанные на ранговых статистиках [6]. После этапа обнаружения элементы изображения, отмеченные как выбросы импульсного шума, заменяются их оценкой. В качестве оценки здесь обычно используются значения, полученные тем или иным сглаживанием по окрестности этих элементов, причем из этой окрестности исключаются элементы, отмеченные при обнаружении выбросов шума.
Характерными при сглаживании импульсных помех являются ошибки ложного обнаружения, которые приводят к нежелательному сглаживанию деталей изображения, и ошибки пропуска, из-за которых на изображении могут остаться несглаженные выбросы помех. Это обуславливается применением
низкоэффективных методов обнаружения помех и недостаточно точным их восстановлением, не учитывающим корреляционные свойства случайного процесса. Также надежность этих методов снижается также из-за возможного наличия в окрестности не одного, а нескольких выбросов помех.
Наличие проблемы пораженных и недостоверных данных в выборке при отсутствии эффективных, а тем более универсальных методов их восстановления и обуславливает, в конечном итоге, актуальность данной работы.
Целью работы являются исследование влияния импульсных помех на качество линейной оценки прогнозирования (ЛОП), а также разработка метода защиты ЛОП от интенсивного потока импульсных помех.
Для достижения поставленной цели в диссертационной работе были рассмотрены следующие задачи:
Вывод и обоснование критерия качества линейной оценки прогнозирования на основе информационной метрики Кульбака-Лейблера;
Анализ влияния случайных импульсных искажений на качество обработки информации при решении задач различного рода с использованием критерия минимума информационного рассогласования (МИР);
Разработка цифрового алгоритма восстановления данных, подверженных воздействиям импульсных помех;
Разработка цифрового алгоритма обнаружения импульсных помех и исследование его эффективности;
Анализ эффективности ЛОП с защитой от ИП в задаче прогнозирования социально-экономических процессов.
Анализ эффективности разработанного алгоритма в задачах подавления комбинированных помех в радиотехнических системах и распознавания речевых сигналов методом обеляющего фильтра.
12 Методы исследования. При решении поставленных задач использовались
методы теории вероятностей и математической статистики, теории
информации, а также метод математического моделирования в лабораторных и
натурных условиях с применением разработанного программного пакета на ПК.
Научная новизна диссертационной работы состоит в следующих
полученных результатах:
Разработан критерий критерия минимума информационного рассогласования для оценки динамических свойств линейной оценки прогнозирования;
Исследована проблема наличия импульсных помех в выборке и подтверждена ее актуальность;
Разработан цифровой алгоритм восстановления данных, подверженных воздействиям импульсных помех;
Исследовано влияние основных параметров импульсных помех на качество обработки информации;
Проведен анализ эффективности разработанного алгоритма с использованием предложенного критерия минимума информационного рассогласования;
Обосновано преимущество разработанного алгоритма по сравнению с традиционными алгоритмами борьбы с импульсными помехами.
Практическая ценность работы состоит в разработке и исследовании новых алгоритмов защиты от импульсных помех, а также реализации программного пакета автоматизированной системы обработки данных и прогнозирования «Invest-XP», предназначенного для решения широкого круга практических задач. Практическая ценность диссертационной работы подтверждается актами об использовании ее результатов в учебном процессе Нижегородского государственного лингвистического университета и Нижегородского государственного технического университета.
Основные результаты диссертационной работы апробированы в докладах на научных конференциях:
- II Всероссийской НТК "Методы и средства измерений физических
величин" (Н. Новгород, НГТУ, 1997);
Всероссийской НТК посвященной 80-летию нижегородской радиолаборатории (Н. Новгород, НГТУ, 1998);
Всероссийской конференции "Общие проблемы управления и их применение к математической экономике "ОПУ-2000" (Тамбов, ТГУ, 2000);
V Всероссийской НТК "Методы и средства измерений физических величин" (Н. Новгород, НГТУ, 2000);
V Всероссийской НТК "Информационные технологии в науке, проектировании и производстве" (Н. Новгород, НГТУ, 2002).
По материалам диссертации опубликовано 10 научных работ, в том числе 4 статьи, кроме того, при участии автора было подготовлено и опубликовано учебное пособие.
Диссертация состоит из введения, четырех глав, заключения, списка литературы и приложения.
В первой главе ставится и решается задача оптимального прогнозирования СВР, рассматривается понятие линейной оценки прогнозирования на основе линейной авторегрессионной модели, описывается алгоритм оценивания АР-параметров на основе метода максимальной энтропии, исследуются динамические свойства алгоритма прогнозирования, рассматривается проблема малых выборок, обосновывается выбор информационного критерия эффективности оценки прогнозирования в условиях ограниченных выборок наблюдений.
Во второй главе ставится и решается задача автоматического восстановления данных, искаженных воздействием импульсных помех, приводится анализ влияния импульсных помех на динамические свойства линейной оценки прогнозирования, исследуется эффективность предлагаемого метода в задаче прогнозирования случайных процессов на примере процесса типа «авторегрессия» с использованием критерия МИР.
14 В третьей главе ставится задача обнаружения импульсных помех,
обосновывается выбор метода обнаружения импульсных помех на основе
спектрального оценивания, рассчитываются его основные характеристики,
проводится анализ его эффективности по сравнению с другими методами
обнаружения помех.
В четвертой главе описана автоматизированная система обработки информации и прогнозирования, рассмотрены примеры применения предлагаемого алгоритма при решении некоторых практических задач: прогнозирования социально-экономических процессов, распознавания речевых сигналов и подавления пассивных помех в системах СДЦ.
Каждая глава завершается перечислением основных полученных результатов и выводами.
В заключении сформулированы основные результаты работы и выводы по теме исследований, а также даны предложения по их практическому применению и дальнейшему развитию.
В приложении помещены акты использования результатов диссертационной работы.
Анализ динамических свойств. Теоретико-информационный подход
Полученное выражение называется уравнением Юла-Уокера [44] и определяет оптимальное в смысле минимума дисперсии ошибки прогнозирования значение вектора коэффициентов а в линейной оценке прогнозирования (1.4). Видно, что его значение зависит исключительно от корреляционных свойств анализируемого ВР X(t).
К сожалению, на практике, как правило, мы не имеем достоверных сведений о корреляционных свойствах процесса X(t). В условиях априорной неопределенности возникает необходимость в оценивании коэффициентов автокорреляции в выражении (1.6) по имеющейся выборке наблюдений.
Проблема состоит в том, что в пересчете к результирующей ошибке прогнозирования погрешности оценивания АР-коэффициентов многократно усиливаются, особенно при большом порядке АР-моделей. Поэтому такие известные методы авторегрессионного анализа, как метод наименьших квадратов, Блэкмана-Тьюки и другие, весьма эффективные при иных обстоятельствах, применительно к задаче прогнозирования часто не обеспечивают приемлемых для практики результатов. Сделанный вывод строго обосновывается в законе «большого параметра» [42]: сфера применения адаптивного подхода в классической интерпретации ограничивается кругом задач, в которых отношение N/M»\, т.е. при весьма больших объемах наблюдений. В зависимости от применяемого способа оценивания параметров АР модели получают различные модификации линейной оценки прогнозирования. При этом достигаемая скорость ее сходимости к оптимальному виду описывается степенным законом и неулучшаема по порядку /дг- Причем указанное свойство характерно для всех без исключения новых методов. Проблема поиска оптимального прогноза таким образом переходит в совершенно иную плоскость: поскольку в асимптотике, т.е. при бесконечном объеме выборки наблюдений, все известные методы дают одинаковые оценки коэффициентов авторегрессии, то основное различие между методами заключается в их быстродействии или скорости сходимости выборочных оценок к их истинным значениям. К сожалению не все задачи, особенно задачи экономического анализа, отвечают данному требованию. Для многих задач характерным является противоположный случай N/M 10 [39, 77]. Во-первых, число используемых наблюдений ограничено конечной длиной интервалов стационарности социально-экономических процессов. Во-вторых, порядок АР-моделей (1.3) вынужденно устанавливается заведомо большим, чтобы учесть все основные действующие в реальных процессах закономерности [57]. И, в-третьих, вышеописанные проблемы обостряются в значительной степени при наличии в обозримой ретроспективе выборочных данных одного или нескольких недостоверных отсчетов, например, отсутствующих, или пораженных импульсными помехами. В указанных условиях необходим иной подход, принципиально нацеленный на обработку конечных массивов данных. И такой подход существует в информационной теории адаптивного спектрального оценивания случайных процессов и полей, построенных вокруг принципа минимакса энтропии наблюдений [55] и информационного критерия оптимальности АР модели. Вернемся к исходному уравнению авторегрессионной модели (1.3) и перепишем его в инверсном виде Полученное уравнение можно рассматривать как линейное преобразование случайного процесса - (0 в «белый» или независимый шум r/{t). Преобразование такого рода называется «обелением» или декорреляцией случайных процессов [1, 44]. Практической реализацией декорреляции служит линейный обеляющий фильтр. В контексте сказанного уравнение (1.7) описывает динамику трансверсального обеляющего фильтра М-го порядка с постоянными коэффициентами ах,...,ам. Задать такой фильтр - это значит задать его вектор весовых коэффициентов. С другой стороны, задаваясь обеляющим фильтром вполне определенной структуры (1.7), одновременно будем иметь соответствующий вариант прогноза (1.4). Поэтому задача прогнозирования в формулировке (1.4)...(1.6) может быть сведена к эквивалентной задаче поиска оптимальной структуры обеляющего фильтра (1.7). В условиях априорной неопределенности относительно истинных параметров АР-модели (1.3) искомый обеляющий фильтр должен быть выполнен в адаптивном варианте, предполагающим заданный алгоритм настройки его параметров ах,...,ам по имеющейся выборке наблюдений. В основе таких алгоритмов применяются разнообразные методы стохастической аппроксимации [87, 88]. Причем предпочтение отдается методам с улучшенными динамическими свойствами, ориентированным на обработку небольших массивов данных. Наиболее впечатляющие результаты в этом перспективном научном направлении достигнуты в области синтеза и анализа адаптивных методов нелинейного спектрального оценивания [44]. Разработанные здесь в рамках универсального теоретико-информационного подхода методы авторегрессионного анализа, такие как методы линейного предсказания, максимальной энтропии, максимального правдоподобия и другие, используют обеляющий фильтр в качестве ключевого звена адаптивной обработки информации. По своим скоростным характеристикам они намного превосходят классический метод наименьших квадратов. Благодаря такому обстоятельству открываются реальные возможности для преодоления проблемы малых выборок наблюдений [55].
О влиянии случайных импульсных искажений на точность и динамические свойства линейной оценки прогнозирования
Параметры линейной оценки прогнозирования были установлены следующим образом: порядок модели М=\0, а объем выборки варьировался в широких пределах N=20.. .300.
На рис. 2.4 различные кривые соответствуют различным параметрам помех, причем сплошными линиями показаны кривые адаптации при наличии помех в исследуемой выборке (кривые 2 и 3) при различных их параметрах, а пунктирной линией (кривая 1) показана кривая адаптации, но в отсутствие помех.
Из графиков видно, что даже при низкой интенсивности помех и их дисперсии, много меньшей дисперсии входного процесса, мы имеем значительное отклонение от кривой, полученной в отсутствие помех, причем в худшую сторону. Также можно заметить, что повышение интенсивности помех приблизительно эквивалентно возрастанию их дисперсии. Особенно сильное влияние на качество линейной оценки прогнозирования помехи оказывают при малых объемах выборки.
Характер зависимости величины информационного рассогласования от интенсивности импульсных помех можно проиллюстрировать с помощью полученных результатов, показанных на рис. 2.5. Результаты были получены также для АР-процесса 10-го порядка при использовании выборки небольшого объема 7V=100. Из рисунка видно, что при увеличении интенсивности помех информационное рассогласование также увеличивается. Причем закон этой зависимости близок к линейному. Проблема малых выборок в данном случае обостряется ещё в более значительной степени при увеличении интенсивности помех.
Вышеописанные экспериментальные исследования над АР-моделью ещё раз подчеркивают актуальность проблемы наличия пораженных отсчетов в выборке. Очевидно, что даже при незначительных интенсивностях и мощностях помех не удается получить точную оценку прогноза поведения анализируемого процесса в будущее, особенно при небольших объемах выборки.
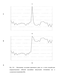
Поскольку, в результате, наши исследования направлены на получение качественного прогноза, точно описывающего динамику исследуемого процесса, проанализируем, как, в конечном итоге, импульсные помехи влияют на искомую динамику прогноза. Это влияние показано на рис. 2.6, благодаря проведенному эксперименту над анализируемым АР-процессом Х{п). Его порядок М был установлен равным 10. Для расчета оценки прогнозирования использовалась АР-модель такого же порядка Л/=10. Для моделирования импульсных помех использовались отсчеты БГШ с дисперсией о ип = Jex .
На графике (рис. 2.6) пунктирной линией (кривая 1) отображен участок входного процесса, а кривая 2 соответствует прогнозам на 10 шагов в будущее в отсутствии помех. Кривая 3 на рисунке показывает прогнозы входного процесса, подверженного действию импульсной помехи.
Видно, что импульсное искажение отсчетов кардинальным образом меняет динамику прогноза даже в случае однократного воздействия ИП. Несомненно, данный прогноз является непригодным для дальнейшего использования.
При этом возникает естественный вопрос о природе влияния помех на оценки прогнозирования при использовании обеляющего фильтра для получения неизвестных АР-параметров модели. Всё дело в том, что в рассмотренном случае помеха дважды воздействует на качество получаемой линейной оценки прогнозирования:
При настройке АР-параметров в адаптивном фильтре. Такое воздействие помехи будет продолжаться в течение времени, соответствующее N отсчетам, где N — объем выборки, используемой для обучения фильтра. В этом случае вектор АР-параметров { 2j} не сможет настроиться должным образом, и полученная АР-модель анализируемого процесса не будет должным образом соответствовать самому процессу;
Непосредственно при прогнозировании пораженный отсчет может входить в формулу (1.4), то есть иметь индекс (/7-М),..., (я-1). В этом случае помеха напрямую влияет на оценку прогноза. А т.к. всегда выполняется соотношение M N (порядок модели всегда меньше, чем объем обучающей выборки), то это воздействие всегда усугубляется воздействием, описанным выше (пункт 1). Причем, чем выше порядок модели М, тем более продолжительным будет это воздействие. Другими словами, чем выше сложность анализируемого процесса, и, следовательно, выше порядок модели, тем сильнее влияние помехи на качество получаемых оценок прогнозов. С другой стороны, искусственное занижение порядка АР-модели приводит к тому, что она становится неадекватной анализируемому процессу и непригодной для использования при его прогнозировании.
Все вышесказанное подтверждается рядом кривых на рис. 2.7. На рисунке кривая 2 показывает временную зависимость величины информационного рассогласования анализируемого процесса и линейной оценки прогнозирования (п+\)-го отсчета, полученную в момент времени п при воздействии импульсной помехи в момент времени n=tn. Для сравнения, кривая 1 показывает среднее значение информационного рассогласования при прогнозировании процесса без помех. Кривые были получены путем усреднения 1000 соответствующих результатов экспериментов над АР-процессом 10-го порядка. Порядок АР-модели был также установлен равным М—Ю. Из рисунка видно, что влияние помехи распространяется на длительный временной интервал n tn, а не только на момент времени действия помехи, и не ограничивается моментом времени n=tu+M.
Таким образом, благодаря проведенным экспериментальным исследованиям над процессом типа «авторегрессия», удалось однозначно выявить негативное воздействие импульсных помех на точность прогнозирования. А так как класс авторегрессионных процессов является достаточно широким для того, чтобы охватить множество реально существующих процессов, то, несомненно, импульсные помехи будут уменьшать качество обработки сигнала даже при единичном своем воздействии. Это, в конечном итоге, может привести к негодности получаемых оценок к использованию. Чтобы уменьшить это влияние, необходим механизм устранения помех, который позволит восстановить всю имеющуюся последовательность выборочных данных.
Задача обнаружения разладки случайного временного ряда
Программа экспериментов включала в себя исследование динамических свойств алгоритма прогнозирования в случае наличия случайных импульсных искажений в данных. Программа исследований содержала также анализ эффективности предложенного алгоритма восстановления данных в зависимости от параметров импульсных помех.
Выводы теоретических исследований получили подтверждение по результатам ряда проведенных экспериментов над анализируемым процессом Х{п) типа "авторегрессия" 10-го порядка. Как и в проведенных экспериментах (рис. 2.4 - 2.7), входная последовательность формировалась согласно блок-схеме на рис. 2.2.
Следует отметить, что нижеописанные эксперименты проводились при условии известности всех моментов действия помех. Это позволяет исследовать обоснованность самой идеи восстановления данных независимо от метода обнаружения помех. Естественно, что при использовании различных методов обнаружения помех, будем иметь результаты, имеющие различную надежность.
Рассмотрим вначале изменение динамики прогноза АР-процесса при использовании предлагаемого алгоритма для вышеописанного случая (рис. 2.6). При проведении эксперимента пораженные отсчеты восстанавливались по формуле (2.8). Результаты эксперимента показаны на рис. 2.9. На графике пунктирной линией показан участок АР-процесса, кривая 1 показывает прогноз на 10 шагов в будущее при отсутствии ИП, кривая 2 - при их наличии, а кривая 3 - результат, полученный при задействовании алгоритма восстановления. Проанализировав полученный результат, можно придти к выводу, что благодаря применению метода восстановления пораженных данных удается практически полностью устранить влияние помех на точность прогнозирования динамики процесса типа «авторегрессия». При этом изменения в динамике и точности прогноза по сравнению с результатами, описанными кривой 1 (при отсутствии помех), являются незначительными. Видно, что в данном случае удалось восстановить пригодность прогноза к дальнейшему использованию.
Дополнительно были получены количественные характеристики эффективности предлагаемого алгоритма при различных параметрах импульсных помех. Результаты показаны на рис.2.10. На графике можно выделить зависимости величины информационного рассогласования адаптивной оценки прогнозирования при различных параметрах потока помех без восстановления отсчетов (кривые 2 и 3) и при использовании алгоритма восстановления (кривые 2 и 3 ) от объема обучающей выборки N Результаты были получены путем последовательного восстановления отсчетов по формуле (2.8). Дополнительно на рисунке 2.11 представлены зависимости величины информационного рассогласования от интенсивности потока импульсных помех / при использовании алгоритма их устранения (кривые Г и 2 ). Сравнивая эти графики с аналогичными кривыми, полученными без устранения ИП (кривые 1 и 2), приходим к выводу, что эффективность предлагаемого алгоритма возрастает при увеличении интенсивности помех и при увеличении дисперсии потока. При этом, абсолютное значение величины удельного информационного рассогласования увеличивается незначительно как при увеличении интенсивности помех /, так и при увеличении их мощности тип .
Благодаря использованию предлагаемого метода восстановления, нам удается значительно улучшить скоростные характеристики адаптивной оценки прогнозирования при любых параметрах помех и объеме выборки. Для иллюстрации метода восстановления по формуле (2.8) и ранее описанного метода (формула (2.6)) приведем результат их сравнения, показанный на рис.2.12. Здесь кривая 1 описывает кривую адаптации при восстановлении пораженных отсчетов путем их замены значением прогноза на предыдущем шаге (формула (2.8)), 2 - при восстановлении по формуле 2.6. Из графика видно, что, в целом, оба метода могут быть признаны эффективными при некотором преимуществе интерполяционного метода восстановления (2.6). Однако применение упрощенной формулы (2.8) не приводит к значительным ухудшениям динамических свойств ЛОП. Таким образом, воздействие импульсных помех приводит к существенному ухудшению качества обработки сигнала, причем, чем выше интенсивность потока импульсных помех, тем больше это влияние. Применение алгоритма с восстановлением отсчетов пораженного сигнала эффективно защищает систему от воздействия импульсных помех. Причем выигрыш возрастает при увеличении интенсивности и мощности импульсных помех. 1. Воздействие случайной последовательности импульсных помех в существенной степени ухудшает качество линейной оценки прогнозирования, а также ее динамические свойства. При этом эффективность применения методов с высокими динамическими характеристиками практически сводится к нулю. Особенно сильно влияние помех при небольших объемах выборки, используемой в процессе настройки адаптивного фильтра, что значительно усугубляет и без того остро стоящую проблему малых выборок. 2. Синтезированный алгоритм восстановления искаженных выборочных данных позволяет практически полностью устранить негативное влияние действия импульсных помех на качество обработки сигнала, в частности, прогнозирования случайных процессов. При этом удается значительно снизить информационное рассогласование используемой модели и исследуемой выборки данных. 3. Путем математического моделирования с использованием в качестве входного сигнала процесса типа «авторегрессия» доказана высокая надежность предложенного алгоритма. Причем достигаемый эффект - улучшение точности прогнозирования в условиях действия ИП. Этот эффект возрастает при увеличении интенсивности помех по частоте повторения /, а также их мощности УИП .
Задача селекции движущихся радиолокационных целей на фоне комбинированной помехи
Инвесторы опасались, что снижение ставок приведет к падению прибыли компании.». Это позволяет нам предполагать, что данный выброс не приведет к долгосрочным изменениям статистических свойств процесса, а является единичным проявлением реакции рынка на некоторый положительный фактор. После восстановления отсчета, полученного 01.10.2002, нам удалось получить более качественный прогноз в смысле описания динамики поведения анализируемого процесса на следующие 10 торговых дней (кривая 3 на рис. 4.8).
Однако наличие процедуры восстановления не является гарантией получения качественных прогнозов в любой ситуации. Более того, точность получаемых прогнозов может варьироваться в широких пределах в зависимости от ситуации.
Предлагаемый алгоритм позволяет в режиме реального времени отслеживать изменения структуры временного ряда и свести к минимуму вероятность получения неадекватных прогнозов. Тем самым появляется возможность, не отрицая самой идеи прогнозирования и не отказываясь от прогнозов вообще, устанавливать для конкретных ситуаций при решении практических задач ту или иную степень "доверия" к прогнозам. К получаемым после восстановления прогнозам следует относиться с особой осторожностью, используя их в совокупности с альтернативными прогнозами, полученными без восстановления.
Всё-таки основной целью прогнозирования экономических рядов является не следование руководствам прогноза, а лишь дополнительное обосновании уверенности трейдера в предвидении поведения рынка при планировании операций на рынке ценных бумаг. И лишь при использовании совокупности экономического, политического и технического типов анализа появляется возможность успешной работы на рынке.
Обнаружение движущихся целей на фоне пассивных помех является одной из важнейших проблем, с которыми приходится сталкиваться при разработке РЛС различного назначения. Одним из научных направлений в решении указанной проблемы является теория обнаружения сигналов на фоне помех, которая располагает методами анализа и синтеза алгоритмов обработки в устройствах селекции движущихся целей (СДЦ) и в адаптивных антенных решётках (ААР), а также методами адаптивной цифровой фильтрации.
В настоящее время для обработки радиолокационной информации широко применяются цифровые методы, что обусловлено рядом преимуществ этих методов по сравнению с аналоговыми. Развитие цифровых методов позволило повысить эффективность устройств СДЦ за счёт создания радиолокационных карт помех, применения вобуляции частоты повторения, использования быстрых дискретных преобразований, в частности быстрого преобразования Фурье (БПФ).
В настоящее время продолжаются интенсивные теоретические и экспериментальные исследования адаптивных цифровых устройств (АЦУ) СДЦ, способных обнаруживать цели на фоне пассивных помех с изменяющимися в широких пределах во времени и в пространстве характеристиками. При этом в перечисленных источниках в качестве перспективных рассматриваются алгоритмы параметрической оценки, максимальной энтропии, процедуры ортогонализации Грама-Шмидта и использования БПФ.
Непреходящий интерес к синтезу адаптивных алгоритмов обработки свидетельствует о том, что проблема полностью не решена и поиски адаптивных алгоритмов, удовлетворяющих противоречивому требованию получения максимального ОСПШ при минимальных вычислительных затратах, ведутся в различных направлениях. Для подавления пассивных помех в РЛС применяются различные устройства и методы. Они должны обеспечивать эффективное выделение сигнала при воздействии различных пассивных помех и их комбинаций. Первоначально устройства СДЦ предназначались исключительно для подавления отражений от местных предметов. В настоящее время их роль и предъявляемые к ним требования существенно возросли. Задача современных систем СДЦ - подавление пассивных помех любых видов. Проектирование современных РЛС во всё большей степени идёт по пути применения адаптивных принципов в двух основных направлениях, характеризуемых: способностью РЛС автоматически фиксировать изменение рабочих условий; способностью автоматической установки параметров, включая форму зондирующих сигналов, их поляризацию, методы обработки эхо-сигналов, форму диаграммы направленности и чувствительность приёмного тракта. Вопросы адаптации, таким образом, касаются анализа помеховой обстановки с одной стороны, и способности перестройки в реальном масштабе времени схемы РЛС для обеспечения постоянного уровня ложных тревог с другой. Вторая часть задачи решается как при изменении формы зондирующих сигналов, так и при изменении методов обработки эхо-сигналов. С точки зрения временных характеристик процесса можно рассматривать: статическую адаптивность к мешающим отражениям, практически неподвижным в пространстве и медленно флуктуирующим во времени; динамическую адаптивность к мешающим отражениям, быстро изменяющимся как в пространстве, так и во времени с сильными флуктуациями по амплитуде и доплеровской частоте. Как было уже отмечено, основной задачей, стоящей перед РЛС с СДЦ, является обнаружение целей, движущихся на фоне пассивных помех, определение координат и параметров их движения, а также сопровождение целей. Поэтому при анализе РЛС с СДЦ основными являются целевые показатели эффективности, учитывающие вероятность обнаружения цели и точность определения координат объектов при определенной помеховой обстановке. В режиме обзора наибольшее распространение получили характеристики обнаружения или рабочие характеристики приемника (РХП) РЛС с СДЦ, представляющие собой графические зависимости вероятности обнаружения цели от отношения мощностей сигналов цели и помех при заданных вероятностях ложных тревог.
РХП дают достаточно полную оценку технической эффективности РЛС с СДЦ, недостатком их является сложность определения и недостаточная критичность по отношению к параметрам, оценивающим качество работы основных узлов станций.
К числу вероятностных показателей качества РЛС с СДЦ относится также «пороговый сигнал» - минимальный по величине сигнал, который еще обнаруживается с заданной вероятностью на фоне помехи данного вида и уровня, вызывающий ложную тревогу с фиксированной вероятностью. Отношение «порогового сигнала» к уровню помехи называют «пороговым отношением сигнал - помеха».
Сложность определения вероятностных показателей качества РЛС с СДЦ приводит к тому, что на практике большее распространение получили энергетические показатели, которые, несмотря на присущую им известную ограниченность, имеют достаточно простую физическую трактовку и достаточно просто могут быть определены.