Содержание к диссертации
Введение
Постановка задачи исследования 9
1.1. Задача активной идентификации 9
1.2. Структура математической модели 13
1.3. Современное состояние проблемы активной идентификации стохастических линейных непрерывно-дискретных систем... 15
1.4. Выводы 18
Оценивание неизвестных параметров 20
2.1. Вычислительные аспекты задачи оценивания неизвестных параметров 20
2.2. Алгоритм нахождения значения функции правдоподобия 25
2.3. Алгоритм нахождения значения градиента функции правдоподобия 28
2.4. Выводы 34
Вычисление информационной матрицы одноточечного плана 35
3.1. Вывод соотношения для информационной матрицы одноточечного плана 35
3.2. Алгоритм вычисления информационной матрицы одноточечного плана 52
3.3. Выводы 54
Планирование d- и а- оптимальных входных сигналов 56
4.1. Синтез входных сигналов с использованием методов нелинейного программирования 56
4.1.1. Запись экстремальной задачи 56
4.1.2. Вычисление градиентов критериев оптимальности..,. 58
4.1.3. Синтез оптимальных входных сигналов для системы регулирования температуры в жилом помещении 60
4.1.4. Синтез оптимальных входных сигналов для системы управления боковым движением автобуса 66
4.2, синтез входных сигналов с использованием методов теории планирования экспериментов 73
4.2.1. Теоретические основы 73
4.2.2. Прямая градиентная процедура построения непрерывных оптимальных планов ... 76
4.2.3. Двойственная градиентная процедура построения непрерывных оптимальных планов 79
4.2.4. Синтез оптимальных входных сигналов для системы регулирования температуры в жилом помещении 81
4.2.5. Синтез оптимальных входных сигналов для системы управления боковым движением автобуса 84
4.3. Выводы 89
Активная идентификация на примерах динамических моделей различной природы 91
5.1. Система регулирования температуры в жилом помещении... 92
5.2. Система управления боковым движением автобуса 100
5.3. Выводы 104
Заключение 105
Список использованных источников
- Структура математической модели
- Алгоритм нахождения значения функции правдоподобия
- Алгоритм вычисления информационной матрицы одноточечного плана
- Прямая градиентная процедура построения непрерывных оптимальных планов
Введение к работе
Актуальность темы исследований. Математические модели играют важную роль при изучении различных явлений и создании новых технических систем Еще несколько десятилетий назад при проектировании сложных объектов (самолетов, судов, мостов и др ) использовали в основном физические модели - макеты, то есть уменьшенные копии этих объектов На них проводили многочисленные натурные эксперименты, выявляли слабые и сильные стороны проекта, полученные результаты затем использовали при создании этих объектов
В настоящее время благодаря успехам вычислительной техники и наличию разнообразных математических моделей стало возможно вместо натурных проводить вычислительные эксперименты, которые имеют преимущества перед натурными Они существенно удешевляют и ускоряют процесс проектирования и, как правило, позволяют найти не просто хорошие, а оптимальные решения
Идентификацией динамической системы (процесса) называется получение или уточнение по экспериментальным данным математической модели этой системы или процесса, выраженной посредством того или иного математического аппарата Идентификация проводится обычно в целях облегчения предсказания поведения идентифицируемой системы в будущем Очевидно, что модели могут принимать самую разную форму и записываться с разной степенью математической детализации Выбор того уровня сложности, который делает модель полезной, определяется планируемым использованием
Проблема идентификации является одной из основных проблем теории и практики автоматического управления Первоначально методология построения динамических моделей развивалось в рамках пассивного подхода, при котором идентификация проводилась в режиме нормальной эксплуатации исследуемой системы и заключалась в оценивании неизвестных параметров, входящих в модель Современная теория идентификации включает в себя также методы активной идентификации, сочетающие решение задачи параметрического оценивания с идеями теории планирования эксперимента, повышающими эффективность проводимых исследований
Обозначим основные этапы процедуры активной идентификации динамических систем оценивание параметров модели согласно выбранному критерию идентификации по имеющимся экспериментальным данным соответствующим некоторому начального входного сигналу (пассивная идентификация), построение оптимального по заданному критерию входного сигнала отвечающего вычисленным оценкам (планирование), регистрация выходных данных системы с использованием найденного входного сигнала, пересчет оценок неизвестных параметров В случае необходимости этапы 2-4 повторяются
С начала 70-х годов начинает интенсивно развиваться теория идентификации динамических моделей, опирающаяся на теорию оптимального управления и теорию оптимального эксперимента Современный этап развития теории и практики параметрической идентификации характеризуется все более широким распространением идей и методов активной идентификации Этому способствовали, в частности, труды А Ж Абденова, Ю П Адлера, В Г Горского, В И Денисова, Г К Круга, В Н Овчаренко, А А Попова, Ю А Сосулина, А М Талалая, В А Фатуева, В М Чубича в нашей стране и Дж К Гудвина (G С Goodwin), М Б Зейропа (М В Zarrop), Р К Мехры (R К Mehra ), Р Л Пейна (R L Payne) за рубежом
Для непрерывно-дискретных систем наиболее развиты в теоретическом и прикладном отношениях вопросы планирования оптимальных входных сигналов для детерминированного случая
Вопросы активной идентификации стохастических непрерывно-дискретных систем менее изучены По-видимому, причина во многом обусловлена самой сложностью проблемы
На момент написания настоящей диссертационной работы для многомерных стохастических линейных непрерывно-дискретных систем, описываемых стационарными моделями в пространстве состояний, были сформулированы и доказаны основополагающие теоремы о свойствах информационных матиц, об эквивалентности D- и G- оптимального планирования, получены выражения для элементов информационной матрицы одноточечного плана для случая вхождения неизвестных параметров только в матрицы состояния и управления, предложена прямая градиентная процедура синтеза D-оптимальных входных сигналов
В данной диссертационной работе предпринята попытка распространить концепцию активной идентификации на указанные системы, описываемые стационарными моделями в пространстве состояний, для наиболее общего случая, когда неизвестные параметры в различных комбинациях содержались в матрицах состояния, управления, возмущения, измерения, в начальных условиях и в ковариационных матрицах помех динамики и ошибок измерений, проанализировать целесообразность ее применения, разработать и реализовать соответствующие алгоритмы активной идентификации и исследовать их эффективность на примерах динамических моделей различной природы
Цель исследования. Целью работы является распространение концепции активной идентификации на математические модели многомерных стохастических линейных непрерывно-дискретных систем, а также развитие теоретических и методологических основ этого вопроса
Методы исследования. Теоретические и прикладные исследования базируются на использовании разделов теории планирования эксперимента, математической статистики, теории случайных процессов, вычислительной математики, теории управления и линейной алгебры
Достоверность и обоснованность научных положений, рекомендаций и выводов обеспечивается корректным применением аналитических методов,
результатами исследования процедур активной идентификации с использованием статистического моделирования, решением прикладных задач
Научная новизна. Получены следующие новые результаты, которые выносятся на защиту
получено выражение для информационной матрицы одноточечного плана,
разработан алгоритм вычисления информационной матрицы одноточечного плана,
проведен структурный анализ соотношения для информационной матрицы, позволивший оптимизировать процесс нахождения планов экспериментов,
предложен подход к построению локально-оптимальных входных сигналов, основанный на решении соответствующей задачи нелинейного программирования с ограничениями в классе кусочно-постоянных функций,
на основе прямого и двойственного подходов к планированию разработаны градиентные алгоритмы синтеза D- и А- оптимальных входных сигналов, в которых вычисление производных осуществляется в соответствие с полученными аналитическими соотношениями,
разработана и реализована процедура активной идентификации, позволяющая синтезировать входные сигналы как на основе подхода связанного, с решением задачи нелинейного программирования, так и с помощью методов теории планирования экспериментов,
численные исследования на примерах моделей систем регулирования температуры в жилом помещении и управления боковым движением автобуса позволили сделать вывод о целесообразности и эффективности применения разработанной процедуры активной идентификации
Личный творческий вклад автора заключается в проведении исследований, обосновывающих основные положения, выносимые на защиту, в разработке программного обеспечения
Практическая полезность и реализация результатов работы. Разработанное программно-математическое обеспечение может использоваться для решения задачи активной идентификации стохастических линейных непрерывно-дискретных систем Отдельные программные модули могут быть использованы для решения задач параметрической идентификации и синтеза D- и А- оптимальных входных сигналов, а также сигналов в соответствии с другими критериями оптимальности Отечественные или зарубежные аналоги разработанного программного обеспечения нам не известны
Полученные результаты исследований используются в учебном процессе при проведении лекционных занятий по курсу «Математические методы планирования эксперимента» для магистрантов, а также при выполнении дипломных работ и магистерских диссертаций студентами, обучающимися по направлению подготовки 010500 - прикладная математика и информатика в Новоси-
бирском государственной техническом университете (НГТУ), что подтверждается актом о внедрении
Апробация работы. Основные результаты диссертационной работы опубликованы в ряде статей, докладывались и обсуждались на следующих всероссийских конференциях научной конференции молодых ученых «Наука Технологии Инновации» (Россия, Новосибирск, 2003), научно-технической конференции «Информатика и проблемы телекоммуникаций» (Россия, Новосибирск, 2007), а также на научных семинарах кафедры прикладной математики НГТУ
Публикации. По материалам диссертации опубликовано 8 печатных работ, в том числе 2 - в ведущих научных журналах и изданиях, входящих в перечень, рекомендованный ВАК РФ, 4 - в сборниках научных трудов, 2 - в материалах всероссийских конференций
Диссертационная работа выполнялась при финансовой поддержке Министерства образования и науки РФ в рамках программы «Развитие научного потенциала высшей школы» (код проекта РНП 2 1 2 43)
Структура и объем работы. Диссертация состоит из введения, пяти глав основного содержания, заключения, списка использованных источников из 67 наименований и двух приложений Общий объем диссертации составляет 129 страниц, включая 8 таблиц и 29 рисунков
Структура математической модели
В пространстве состояний математическая модель динамической системы включает в себя модель состояний (модель динамики) и модель наблюдений.
Рассмотрим следующую непрерывно-дискретную линейную стационарную модель управляемой, наблюдаемой и идентифицируемой динамической системы в пространстве состояний: x(t) = Fx(t)+Gu(t) + rw(t), t є [t0,Tl y(tk)=Hx(tk)+v(tk), k = l,2,...,N, где x(t) - п-вектор состояния системы в момент времени t; u(t) - r-вектор управления; w(t) - р-вектор возмущения; y(tk) - m-вектор измерений в момент tk; v(tk) - m-вектор ошибок измерений. Будем считать, что F, Г, G, Н - соответственно матрицы состояния, возмущения, управления и наблюдения системы требуемых размеров; F устойчива (собственные значения A,j матрицы F удовлетворяют условию Re Я, j 0); пары (F,G) и (F,r) управляемы: rg[GFG...Fn-IGj=n и rg[rFr...[Fn_1rJ=n; пара (F,H) -наблюдаема: rg Нт FTHT і... /1-1 Нт =п; случайные процессы (w(t),t[t0,T]} и {v(tk),к = 1,2,...,N} являются стационарными белыми гауссовскими шумами, причем E[w(t)]=0, Elw(t)wTWj=Q5(t), (1.2) E[v(tk)] = 0, E[v(t, T(tj)J=R5kj, (1.3) E[v(tk)wT(t)J=0, Vtk,t, где 8(t- т) - дельта-функция Дирака; 5;k - символ Кронекера; Q, R неотрицательно-определенная и положительно-определенная матрицы интенсивностей помех размеров рхр и mxm соответственно; начальное состояние x(t0) имеет нормальное распределение с математическим ожиданием E[x(t0)] = xo (1.4) и ковариационной матрицей E{[x(t0)-xo]-[x(t0)-xo]Tj=Po (1.5) и не коррелирует с w(t) и v(tk) при любых значениях переменных t Htk.
Структура модели (1.1) известна с точностью до неизвестных параметров 0 = (0 02,...,05), которые могут входить в различных комбинациях в матрицы F, G, Г, Н, а так же в ковариационные матрицы Q, R и начальные условия хо, Ро Необходимо для математической модели (1.1) с учетом высказанных априорных предположений (1.2)-(1.5) разработать процедуру активной идентификации, исследовать ее эффективность и оценить целесообразность применения этой процедуры для стохастических линейных непрерывно-дискретных систем. Решение этой задачи . потребовало получения аналитических выражений для информационной матрицы Фишера и ее производных по компонентам входного сигнала, разработать соответствующие алгоритмы их вычисления, предложить алгоритмы синтеза оптимальных входных сигналов и разработать соответствующее программное обеспечение.
С начала 70-х годов начинает интенсивно развиваться теория идентификации динамических моделей, опирающаяся на теорию оптимального управления и теорию оптимального эксперимента. Современный этап развития теории и практики параметрической идентификации характеризуется все более широким распространением идей и методов активной идентификации. Этому способствовали, в частности, труды А.Ж. Абденова, Ю.П. Адлера, В.Г. Горского, В.И. Денисова, Г.К. Круга, В.Н. Овчаренко, А.А. Попова, Ю.А. Сосулина, A.M. Талалая, В.А. Фатуева, В.М. Чубича в нашей стране и Дж.К. Гудвина (G.C. Goodwin), М.Б. Зейропа (М.В. Zarrop), Р.К. Мехры (R.K. Mehra ), Р.Л. Пейна (R.L. Payne) за рубежом.
Алгоритм нахождения значения функции правдоподобия
Введем в рассмотрение обновляющую последовательность и ее ковариации: e(tkje)=y(tk)-M{y(tk)y(tk_1),y(tk_2),...,y(t1)}, (2.8) B(tk,e) = M tk,e)sT(tk5e)j. (2.9) Они могут быть определены при помощи фильтра Калмана для системы (1.1) по следующим уравнениям [30, 31, 56]: ix(ttk_1) = Fx(ttk_1)+Gu(t), tk_, a tk, x(t0t0)=xo, (2.10) at p(ttk_1)=FP(ttk_1)+p(ttk_1)F + rQrT,tk_1 t tk,P(t0to) = Po.(2.11) at s(tk)=y(tk)-Hx(tktk_,}, B(tk) = HP(tktk_1)HT + R; K(tk) = P(tktk_1)HTB-1(tk), (2.12) x(tktk)=x(tktk4) + K(tk)8(tk}, P(tktk)=[l-K(tk)H]p(tkltk_i). Здесь x(t tk_j) = E[x(t) Y "1 J; tk_! t tk - оценка одношагового предсказания состояния x(t), полученная по измерениям чГ = {y(ti y(t2X-,y(tk-i)}; Р( І к-і) tk_j t tk - ковариационная матрица ошибок одношагового прогнозирования; x(tk tk)= E[x(tk) Y]J - оценка фильтрации состояния x(tk), полученная по измерениям Yj = {y(ti),y(t2),-, y(tk )}? p(tk I tk) -ковариационная матрица ошибок фильтрации. Определим условную плотность распределения вероятности f [y(tk) I Y\ J по уравнениям фильтра Калмана: = /,,1 , exP(-i[y(tk)-y(tktk.1)]TB-1(tk)[y(tk)-y(tkltk-l)]} = V(2;t)sdetB(tk) I 2 J exp-isT(tk)B-1(tkHtk)}; k = 2,3,..,N. (2.13) (27t)sdetB(tk) Заметим, что f[y(ti)]= r— -=-expj- fa OiMti)}. (2.14) Учитывая, что {y(tk), k=l,2,...} - гауссовский процесс и воспользовавшись соотношениями (2.13), (2.14) можно построить функцию правдоподобия L(Y1 0)=f[y(O].f[y(t2)y(tO].f[y(t3)Y12J-..,f[y(tJYrJ= ехр (2,)Tfl(detB(tk))1 2 k=l - hT(h) lihHh)\- (2.15) 2k=l
Для определения неизвестных параметров, необходимо максимизировать функцию L(YJ ; 0] относительно векторного аргумента 0 или, что гораздо удобнее, минимизировать функцию
1. Приведен критерий идентификации, позволяющий решать методом максимального правдоподобия задачи оценивания неизвестных параметров моделей стохастических линейных непрерывно-дискретных систем в наиболее общей постановке, когда неизвестные параметры в различных комбинациях содержатся в матрицах состояния, управления, возмущения, измерения, в начальных условиях и в ковариационных матрицах помех динамики и ошибок измерений.
2. Разработаны и подробно изложены алгоритмы вычисления логарифмической функции правдоподобия и ее градиента с использованием уравнений фильтра Калмана.
3. Представлен обзор методов нелинейного программирования, использующихся для решения задачи оптимизации функции правдоподобия.
4. Обеспечено выполнение этапа процедуры активной идентификации, отвечающего параметрическому оцениванию.
С математической точки зрения задача синтеза оптимального входного сигнала представляет собой задачу оптимизации некоторого выпуклого функционала от информационной матрицы - (М).
Таким образом, для реализации процедуры активной идентификации необходимо уметь вычислять значение информационной матрицы Фишера М (при фиксированном значение вектора параметров 0).
Теорема. Для математической модели (1.1) с априорными предположениями (1.2)-(1.5), когда неизвестные параметры могут входить в различных комбинациях в матрицы F, G, Г, Н, а так же в ковариационные матрицы Q, R и начальные условия хо, Ро, элементы информационной матрицы плана, сосредоточенного в одной точке, определяются выражениями
Алгоритм вычисления информационной матрицы одноточечного плана
Для многомерных линейных стохастических непрерывно-дискретных систем, описываемых моделями в пространстве состояний, получено выражение (3.1), позволяющее находить элементы информационной матрицы Фишера при наиболее общем характере вхождения неизвестных параметров в модель. 2. Проведен анализ структуры соотношения для информационной матрицы Фишера, позволивший оптимизировать процесс нахождения планов экспериментов. 3. Показано совпадение полученного обобщенного выражения для информационной матрицы Фишера (3.22) с ранее представленными частными результатами из [36, 37]. 4. Разработан алгоритм вычисления значения информационной матрицы одноточечного плана. 5. Заложена основа для построения численных процедур синтеза оптимальных планов для стохастических линейных непрерывно-дискретных систем.
При активной идентификации динамических систем могут использоваться различные способы управления экспериментом, такие как выбор оптимальных моментов измерений, планирование оптимальных входных сигналов, планирование начальных условий [11-12]. Ограничимся задачей планирования оптимальных входных сигналов.
Оптимальный выбор входных сигналов позволяет экспериментатору при заданном числе запусков системы подготовить наиболее информативные данные наблюдений, используемые в дальнейшем для нахождения оценок неизвестных параметров. Отметим, что свобода в выборе входных характеристик существенно различается в зависимости от приложений. В экономических и экологических системах у экспериментатора нет возможности воздействовать на систему с целью проведения идентификационных экспериментов, в то время как в лабораторных условиях и на стадиях разработки нового оборудования выбор входных величин имеет лишь амплитудные и мощностные ограничения.
Планирование оптимальных экспериментов опирается на критерии оптимальности планов. Поскольку в нашем случае структура математической модели динамической системы задана и требуется синтезировать наиболее информативный входной сигнал с тем, что бы повысить точность оценивания неизвестных параметров, можно использовать, например, критерии D- и А-оптимальности [8-11, 13], решая следующую экстремальную задачу: u (t)=arg min Мм(и(1Й]} te=[t0,T], (4.1) u(t)eQu где 4 (11(1),0)) = - 1 det M(u(t),0j в случае критерия D-оптимальности и [M u ), 0j] = Sp M (u(t), 0j для критерия А-оптимальности.
Заметим, что D-оптимальный входной сигнал минимизирует объем эллипсоида рассеивания оценок неизвестных параметров, А-оптимальный -сумму квадратов длин осей и длину диагонали параллелепипеда, описанного около этого эллипсоида.
Поскольку для модели (1.1) информационная матрица M(u(t),)) и сам оптимальный входной сигнал u(t) зависят от оценок неизвестных параметров 0, здесь и далее будем вести речь о локально-оптимальном планировании.
От задач поиска оптимального входного сигнала с непрерывным временем (4.1), следуя методике, изложенной в [47], перейдем к одной из двух следующих задач с дискретным временем [58]: u (ik)= argmin 4 ( ),...,11(1 ),0)] (4.2) u( l)v,u(iN-l) или ч[ч)= argmin [МЦІ!),..., 11(1 ), ,...,TN_I )] (4-3) U( I),-,U(TN-I),TI,-.,-CN-1 при этом будем искать оптимальное управление и(т) в классе кусочно-постоянных функций:
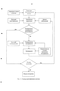
Прямая градиентная процедура построения непрерывных оптимальных планов
Задачу оптимизации (4.18) будем решать методами численного поиска экстремума (см., например, [47-54]). При этом возможны два подхода. Первый из них (прямой) предполагает поиск минимума функционала [м( )] в пространстве элементов информационной матрицы. Характерной его особенностью является большая размерность экстремальной задачи. Поскольку [м( )] - выпуклый функционал, здесь мы имеем задачу выпуклого программирования, для решения которой предлагается следующий алгоритм поиска оптимального решения. Шаг 1. Задать начальный невырожденный план Pi $ = иг ui „о Р2 и о q sUjeQu, р?=-, i = l,2,...,q, q в котором q = — - + 1. Вычислить информационные матрицы M Uj ) одноточечных планов для і = 1,2,..., q и по формуле (4.17) информационную матрицу всего плана о Положить 1 = 0. Шаг 2. Считая веса pj, р2, ...,рі фиксированными, для задачи [м(У- min , UJeQu, i = l,2,...,q uj,...,uj, выполнить одну итерацию метода проекции градиента [53]: 01+1 = п0и,+1-р 0х[мЫ]}, где U =(Uj U2 — UlJ - вектор размерности q-N-r; лп (Z) проекция точки z є Rq г на множество QQ ; pj 0 - длина шага. Составить план U = h uj+1 и2+1 ... uq+1 J J J Pi P2 - Pq j где Uj - точки, найденные на шаге 2. Вычислить MUj ], і = 1,2,...,q. ШагЗ. Зафиксировать точки спектра полученного плана и для задачи Чм(іі)]- mm, р!=1, р! 0, i = l,2,...,q Pi»—»Pq i=l выполнить одну итерацию метода проекции градиента Розена p + p -pi AV M ,)], где p = (pi,p2v3Pqj Pi 0 - длина шага, А - матрица оператора проектирования. Составить план Шаг 4. Если выполняется неравенство q s i=lL UJ -Ш +\pi -pi) 5, где 8 - малое положительное число, перейти на шаг 5. В противном случае для 1 = 1 + 1 повторить шаги 2 и 3. Шаг 5. Поверить необходимое условие оптимальности плана: Ни!+и1+1)-л 5, i = l,2,...,q. (4.19)
Если оно выполняется, закончить процесс. В противном случае повторить все сначала, скорректировав начальное приближение 0.
Соответствие значений параметров [М )], i(U, ), г прямой процедуры критериям D- и А-оптимальности такое же, как в табл. 4.5. Приведенный алгоритм требует вычисления градиентов V0T[Mfe)] = F[Mfe)] auj(tk) , k=0,...,N-l, j=l,...,r; (4.20) Vp[Mfe)b apj , i=l,...,q. (4.21)
Выражения для градиентов (4.20) получены в п. 4.1.2 и определяются соотношениями (4.5) и (4.7) для критериев D- и А-оптимальности соответственно.
Запишем соотношения необходимые для вычисления градиентов по весам. Начнем с критерия D-оптимальности: Другой подход (его называют двойственным) к решению оптимизационной задачи основан на соответствующих теоремах эквивалентности и заключается в минимизации [М )] по набору q аргументов {UjjpJjLj при ограничениях U;Qxj, р; 0, 2ІРІ=1. В і=1 этом случае рассматриваемая задача уже не является задачей выпуклого программирования, но размерность вектора варьируемых параметров может оказаться значительно меньше, чем при прямом подходе. Шаг 1. Задать начальный невырожденный план 0 и по формуле (4.17) вычислить нормированную информационную матрицу м( 0) плана. Положить 1 = 0. Шаг 2. Найти локальный максимум U = arg max a(u, ]) методом проектирования градиента. Если окажется, что Ди ,% j-rj 5, закончить процесс. Если ди ,\ ) ц, перейти на шаг 3. В противном случае искать новый локальный максимум.