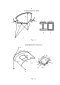Содержание к диссертации
Введение
1. Обзор литературы и состяние вопроса .6
Выводы к разделу 1 15
2. Теоретические исследования неразрезной балки на ступенчато-переменном упругом основании. вывод матричного уравнения 16
Выводы к разделу 2 28
3. Разработка программного обеспечения для расчета на эвм неразрезных балок на ступенчато-переменном упругом основании и его применение к прикладным задачам 29
3.1. Криволинейный брус двутаврового сечения 29
3.2. Криволинейный брус прямоугольного сечения
3.3. Расчет неразрезных балок на упругом основании с применением ЭВМ 33
3.4. Достоверность предлагаемых методов расчета 42
Выводы к разделу 3 48
4. Пространственное нагружение тонкостенных криволинейных узлов рам тележек подвижного состава 50
4.1. Постановка вопроса 50
4.2. Экспериментальное исследование напряженного состояния модели тонкостенного кривого бруса при пространственном нагружении .52
4.3. Методика расчета напряженного состояния криволинейных тонко стенных стержней с деформируемым контуром 59
4.4 Анализ результатов, рекомендации по расчету узлов боковой рамы тележки грузового вагона 66
Выводы к разделу 4 67
5. Применение предлагаемых методов к оценке напряженного состояния реальных конструкций подвижного состава 68
5.1. Расчет напряженного состояния боковой рамы тележки УВЗ-10м грузового вагона 68
5.2. Сравнительная оценка напряженного состояния буксовых проемов различных боковых рам тележек грузовых вагонов 74
5.3. Напряженное состояние несущей балки транспортера сцепного типа грузоподъемностью 340т 94
Выводы к разделу 5 101
6. Экономическая эффективность работы 103
6.1. Оценка экономического эффекта 103
Выводы к разделу 6 106
Заключение 107
Список использованных источнжов
- Криволинейный брус прямоугольного сечения
- Достоверность предлагаемых методов расчета
- Экспериментальное исследование напряженного состояния модели тонкостенного кривого бруса при пространственном нагружении
- Напряженное состояние несущей балки транспортера сцепного типа грузоподъемностью 340т
Введение к работе
Актуальность темы. Основной задачей железнодорожного транспорта является полное обеспечение страны в перевозках народно-хозяйственных грузов и пассажиров. Проектом Федеральной программы предусмотрено обновление подвижного состава, начиная с 2006 года до 400 локомотивов и 40 тыс. вагонов ежегодно. Подвижной состав нового поколеній должен обладать более высокими техническими показателями (повышение веса, скорости движения поездов и др.). Тем не менее, при повышении требований к подвижному составу он должен остаться прочным и надежным в эксплуатации.
Повышение скоростей движения, увеличение веса поездов и грузоподъемности вагонов, осуществляемые на железнодорожном транспорте, ведут к росту динамических воздействий на ходовую часть экипажей. Поэтому ходовая часть подвижного состава должна быть не только достаточно прочной, но и легкой конструкцией. Существенную роль в создании конструкций рам кузовов и тележек, отвечающих требованиям эксплуатационной практики, играют методы прочностных расчетов, наиболее полно учитывающие условия работы и конструктивные особенности рам подвижного состава.
Наиболее опасными элементами рам подвижного состава являются криволинейные узлы сложного очертания, сопрягающие отдельные прямолинейные участки рам. Подобные узлы имеются у рам тележек электровозов ВЛ8, ВЛ60, ВЛ80, ЧС1, тепловоза ТЭП60, боковых рам ЦНИИ-ХЗ, УВЗ-9м, соединительных и шкворневых балках, грузовых вагонов, главных и соединительных балках железнодорожных транспортеров и др. Многочисленные эксперименты и опыт эксплуатации конструкций подвижного состава показывает, что наибольший уровень напряжения достигают именно в криволинейных узлах.
Расчету наиболее напряженных узлов рам уделяли свое внимание многие ученые, предлагавшие все более совершенные теории и методы. Несмотря на большое число работ задача прочностного расчета рам подвижного состава еще далека от своего завершения. Проведение дальнейших исследований, связанных с совершенствованием методов оценки напряженного состояния конструкций подвижного состава, является несомненно актуальным.
Цель работы. Разработка уточненной методики оценки напряженно-деформированного состояния криволинейных узлов рам подвижного состава для создания обоснованной расчетной базы проектирования новых конструкций локомотивов и вагонов.
Методы исследования. При теоретических и экспериментальных исследованиях использовались: матричный метод решения в строительной механике, теория Е.А. Бейлина - Э.Л. Аксельрада, теория неразрезных балок на сплошном упругом основании.
Научная новизна. Предложена и обоснована усовершенствованная методика прочностного расчета криволинейных узлов рам подвижного состава, отличительной особенностью которой является использование теории изгиба неразрезных балок на ступенчато-переменном упругом основании при вычислении важнейших характеристик поперечных сечений рамы. Подобный подход наиболее точно учитывает реальные особенности работы конструкции.
Создан матричный метод расчета неразрезных балок на упругом ступенчато-переменном основании и составлена программа для ЭВМ реализующая данное решение. Решение подобной задачи в литературе неизвестно.
Предложено при пространственном нагружении рам подвижного состава оценку напряженного состояния узлов проводить согласно теории тонкостенных криволинейных стержней Е.А. Бейлина-Э.Л. Аксельрада, которая позволяет учесть деформацию контура поперечного сечения узла при нагружении из плоскости кривизны и стесненном кручении. В такой постановке указанная задача ранее не рассматривалась.
Практическая ценность. Созданы алгоритмы и программные комплексы, позволяющие наиболее достоверно судить о напряженно-деформированном состоянии конструкций, значительно сократить объем проектных разработок и дорогостоящих натурных испытаний при назначении безопасных геометрических параметров рам. уменьшив одновременно их металлоемкость.
Достоверность результатов исследований подтверждается сравнением расчетных напряжений с экспериментальными. В качестве экспериментальных данных взяты результаты, полученные как в лабораторных условиях на моделях, так и натурных испытаний. Среднее расхождение напряжений составило 10-15%.
Апробация работы. Основные результаты работы доложены, обсуждены и одобрены на межвузовской научно-технической конференции ОмГУПС (Омск, 1998 г.), международной конференции "Численные и аналитические методы расчета конструкций" Самарской государственной архитектурно-строительной академии (Самара, 1998г.), отраслевой научно-технической конференции ''Актуальные проблемы развития железнодорожного транспорта и роль молодых ученых в их решении" РГУПС (Ростов-на-Дону, 1998 г.), научно-практической конференции "Ресурсосберегающие технологии на предприятиях Западно-Сибирской железной дороги" ОмГУПС (Омск, 1999 г.), научно-техническом семинаре кафедр механического факультета ОмГУПС (Омск, 1999 г.).
Публикации. Основное содержание диссертационной работы представлено в 8 печатных работах и 2 отчетах по выполнению научно-исследовательских работ по программе ОмГУПС.
Структура и объем диссертации. Диссертация состоит из введения, шести разделов, заключения с выводами, списка использованных источников (90 наименований) и 1 приложения; изложена на 130 страницах текста, содержит 40 рисунков и 18 таблиц.
Автор считает своим долгом выразить благодарность доцентам кафедры "Прикладная математика и механика" (ОмГУПС) Лавриненко Л.Г. и Андросю-ку СП. за оказанные консультации при работе над диссертацией.
Криволинейный брус прямоугольного сечения
В предыдущих главах диссертации разработана теория неразрезных балок на сплошном упругом основании. Каждый пролет такой балки располагается на своём упругом моментном основании с коэффициентом жесткости г и силовом основании с коэффициентом S, а также характеризуется наличием или отсутствием равномерно распределенной нагрузки. Разработанная теория имеет самостоятельное значение в прочностных расчетах неразрезных балок. Помимо этого нас интересуют и другие аспекты прикладного значения. Так уже отмечалось, что тонкостенные криволинейные стенки рам конструкций подвижного состава, имеющие определенную форму поперечного сечения, согласно математической аналогии /4/ работают в условиях неразрезных балок на упругом основании. В свою очередь коэффициенты жесткости S и г для таких балок связаны с видом бруса и формой поперечного сечения. Кроме того, важной характеристикой при расчете тонкостенных кривых стержней является коэффициент использования поперечного сечения (коэффициент Кармана, коэффициент редукции). Приведем некоторые сведения о вычислении коэффициента редукции, коэффициентов жесткости основания S и г для криволинейных стержней различной формы поперечного сечения.
Рассмотрим одиночный криволинейный стержень двутаврового сечения (рис. 3.1) . Согласно математической аналогии доказана идентичность дифференциального уравнения изгиба цилиндрических стенок криволинейного стержня с дифференциальным уравнением изогнутой оси балки на упругом основании/13/: где v - один из основных параметров кривого бруса; а - коэффициент, зависящий от избранной функции поперечного распределения прогибов. Остальные обозначения понятны из рис. 3.1. В случае отсутсвия внешней нагрузки (Go=0) параметры основания находятся по формулам:
Рассмотрим одиночный криволинейный стержень прямоугольного сечения (рис. 3.2). Рассмотрим одиночный криволинейный стержень прямоугольного се-іения (рис. 3.2).
Дифференциальное уравнение цилиндрических стенок имеет прежний ид (3.1). Однако, в этом частном случае изменяются зависимости для ;арактеристик упругого основания /64/:
В выражениях (3.12), (3.13) коэффициент SP учитывает взаимное влия-;ие деформаций верхней и нижней стенок профиля:
На основе выше приведенной методики (глава 2) была разработана программа расчета неразрезных балок на упругом ступенчато-переменном основании. Программы позволяют реализовать расчеты различных произвольных вариантов неразрезных балок. В том числе возможно реализовать случаи расположения отдельных пролетов неразрезной балки на упругом основании с различными характеристиками постели, различными закреплениями границ участков, наличием или отсутствием на пролете внешней нагрузки. В программе используется методика матричного метода.
Программа реализована на алгоритмическом языке QUICK BASIC и состоит из отдельных модулей. Структура программного модуля, которая включает шесть основных блоков и алгоритм расчета неразрезной балки на упругом ступенчато-переменном основании представлены на рис. 3.3-3.9.
Каждый участок характеризуется параметрами: длиной її, шириной сечения mi, отношением ІІ/ПІІ и интенсивностью распределенной нагрузки .Программа работает в диалоговом режиме. Пользователю для расчета необходимо ввести следующие данные: количество участков, варианты закрепления крайних левого и правого сечений, тип сечения и его геометрические параметры.
Варианты закрепления крайнего левого сечения балки определяется элементами матрицы В, которая формируется переменными bw, Ьф, bM, bQ. Варианты закрепления правого сечения определяются матрицей А из элементов &w5 а р, ам, а 2.
При расчете неразрезной балки без опор, вектор неизвестных (W, ф, М, Q,) для каждого участка при изменении длины формируется в матрице D.
Сложностью задачи при расчете неразрезной балки с опорами заключается в определении дополнительных неизвестных реакций в опорах, для нахождения которых необходимо введение условий на границах участков, сформированных в векторе Сг. Для уменьшения количества неизвестных применяется матрица Сі, позволяющих выразить одно неизвестное через другое.
Использование метода начальных параметров предусматривает опре-деление переменных W, ф, М, Q (вектор АІ) на концах каждого участка, обозначенных в программе До, Аь А2. Вычисление вектора неизвестных в любом
Достоверность предлагаемых методов расчета
Результаты выводятся в виде таблице: граничные точки, прогиб W, угол поворота FI, изгибающий момент М, поперечная сила Q, безразмерная координата положения произвольного сечения KSI.
Ниже в качестве примера даны эпюры прогибов W, углов поворота ф, изгибающих моментов М и поперечных сил Q для неразрезной балки на упругом основании (рис.3.10), которая имеет следующие параметры: S=23,59; г=7,7; 1=28,27; и=2,079 полученные в результате реализации упомянутой выше программы.
Также приведены эпюры прогибов W и изгибающих моментов М для неразрезной балки на упругом ступенчато-переменном основании с промежуточными опорами (рис. 3.11) и без промежуточных опор (рис. 3.12) с различными упругими характеристиками S и г для сечения в виде двутавра. Рассмотренные схемы соответствуют сопряжению различных сочетаний криволинейных и прямолинейных участков узлов подвижного состава.
В результате вычислительного эксперимента были найдены значения коэффициентов жесткости основания S и г, при которых вид эпюр изгибающего момента М по длине балки имеет не характерный вид, так как, известно, что М изменяется по закону близкому к плавной выпуклой кривой. Полученные результаты меняют общепринятое представление из теории расчета балок на упругом основании.
В литературе /64/ имеются данные о результатах экспериментального исследования напряженного состояния модели, представляющей собой сопряжения криволинейного тонкостенного стержня двутаврого поперечного сечения с прямолинейными участками (рис.3.13). Эшоры прогиба W, изгибающего момента М, угла поворота р и поперечной силы Q для однопролётной балки на упругом ступенчато-переменном основании
В соответствии с теорией расчётов тонкостенных рам подвижного состава цилиндрические стенки модели работают в условиях неразрезной балки, состоящей из трёх участков (рис.3.14). Средний криволинейный участок имеет равномерно распределённую нагрузку. Характеристики упругого основания первого и третьего участков определяются зависимостями (3.7), (3.8), а для среднего по формулам (3.2), (3.3).
Произведен расчёт деформаций неразрезных балок в соответствии с разработанной в настоящей диссертации методикой. Для выбранных сечений I и II (см. рис.3.13) вычислены приведенные прогибы для точек принадлежащих как верхней, так и нижней цилиндрическим стенкам модели. По известным приведённым прогибам найдены коэффициенты редукции и в заключение вычислены нормальные напряжения в крайних наиболее напряженных точках сечений.
Результаты расчёта и экспериментальные данные сведены в табл. 3.1. В ней также приведены расчётные напряжения, найденные по прежней методике, не использующей особенностей работы цилиндрических стенок как неразрезных балок на упругом основании. Таблица 3.1
Анализ табл. 3.1 показывает, что предлагаемая методика расчета дает достоверные результаты вычисления напряжений. При этом они оказываются более точными по сравнению с данными, полученными по ранее существующим методикам. Наиболее существенно это заметно при расчете максимальных напряжений во втором сечении.
В настоящей главе разработаны алгоритм и программы расчета тонкостенных криволинейных узлов рам подвижного состава на основе теории неразрезных балок на упругом ступенчато-переменном основании. Приведены зависимости для определения коэффициентов жесткости упругого основания, коэффициента редукции для криволинейного бруса двутаврового и прямоугольного сечения. Дана структура программного модуля, алгоритм расчета неразрезной балки на упругом основании с опорами и без опор, описание программы. Эти программы позволяют определять прогиб, угол поворота, изгибающий момент и поперечную силу в произвольном сечении неразрезной балки, содержащей неограниченное число пролетов, лежащий каждый на своём моментном и силовом упругих основаниях, с различными закреплениями границ участков, наличием или отсутствие на пролете внешней нагрузки. По результатам вычислительного эксперимента построены эпюры внутренних усилий для различных видов неразрезной балки, сделан анализ влияния жесткости основания на внутренние усилия.
В предыдущих разделах настоящей работы использовалась теория изгиба криволинейных тонкостенных брусьев. Подобная задача является плоской. Однако внешняя эксплуатационная нагрузка экипажей подвижного состава представляет собой, в том числе и пространственную нагрузку, что несомненно должно учитываться при прочностных расчетах.
В качестве примера приведем работу конструкции боковой рамы тележки грузового вагона модели 18-755 (осевая нагрузка 245 кН) /37/.
Среди спектра нагрузок, воздействующих на боковую раму в эксплуатации и приводящихся в соответствие с нормами /38, 77/ к эквивалентным статическим, рассматривается и боковая сила Нб=55 кН (рис. 4.1), действующая на наиболее нагруженную буксу при движении в кривой (нагрузки заимствованы из заводского расчета /37/).
В результате оценки напряженного состояния в боковой раме тележки модели 18-755 выявлена основная причина, снижающая прочностную надежность конструкции. Этой причиной являются высокие уровни напряжений при восприятии боковых нагрузок, которые приводят к скручиванию и изгибу из плоскости боковой рамы. Конструкция, в следствии малых моментов сопротивления сечений в местах нижнего и верхнего узлов рессорного проема -не приспособлена к восприятию этих нагрузок. К тому же, открытый профиль консольной части буксового проема плохо реагирует на скручивание." Он же отмечает, что изображенный на схеме случай (рис. 4.1) является самым неблагоприятным, напряжения во внешнем углу буксового проема достигают уровня (ОІ, сгь а3)=(201,116,-116) МПа.
Аналогичные выводы делает и ряд других авторов /17, 18, 23/ которые отмечают, что в эксплуатации наблюдаются случаи появления продольных трещин в верхней части буксового проема. Это свидетельствует о возникновении дополнительных напряжений вследствие скручивания боковой рамы при прохождении экипажем кривых малого радиуса. Это подчеркивает необходимость расчета конструкции на пространственное нагружение и возникающее при нем кручение.
Вопросы расчета боковой рамы литой тележки на скручивание и изгиб из плоскости неоднократно поднимались в литературе. Предложения по расчету колонки рамы на стесненное кручение были сделаны Л.А.Шадуром /1/. Идеи этого метода нашли отражение в инженерной практике и в учебниках по проектированию вагонов /36, 43, 75/.
Тем не менее предлагаемые методики не были достаточно совершенны. Как правило, тонкостенные элементы рамы рассчитывались на стесненное кручение при сохранении гипотезы о неизменности жесткости контура поперечного сечения. В тоже время в конце 60-х, начале 70-х годов была разработана теория тонкостенных стержней /12, 69, 70, 71/, в которой показано, что деформация контура тонкостенного сечения может возникать и при нагружении стержня из плоскости кривизны и при стесненном кручении. Более того доказано, что деформация контура и в этом случае может существенно повлиять на напряженное состояние стержня.
Однако до последнего времени эта теория не нашла достойного приложения в расчетах конструкций подвижного состава. Настоящая глава пытается восполнить указанный пробел.
Для доказательства достоверности предлагаемых зависимостей изготовлена и испытана модель тонкостенного кривого бруса при нагружении из плоскости кривизны, а также выполнен ряд расчетов по оценке напряженного состояния как модели, так и некоторых узлов рам подвижного состава.
Экспериментальное исследование напряженного состояния модели тонкостенного кривого бруса при пространственном нагружении
Для анализа напряженного состояния тонкостенного кривого бруса при пространственном нагружении проведены экспериментальные исследования. С этой целью изготовлена модель - кривой тонкостенный брус (материал -сталь; модуль упругости Е = 2-Ю5 МПа; коэффициент Пуассона ц = 0,3) (рис. 4.2), сечение которого имеет форму замкнутой прямоугольной коробки (рис. 4.3).
Экспериментальное исследование напряженного состояния модели тонкостенного кривого бруса при пространственном нагружении
Анализ полученных эпюр по результатам эксперимента показывает, что наибольшие продольные напряжения возникают в сечении П-П, VI-VI, а наибольшие поперечные в сечении IV-IV.
Характерно плавное увеличение напряжений вдоль горизонтальной стенки контура поперечного сечения, которые принимают максимальное значение в наиболее близкой точке к центру кривизны и составляют в сечениях П-П и VI-VI - 478 кгс/см2; Ш-Ш и V-V - 375 кгс/см2; 1-І и VII-VII-268 кгс/см2. Напряжения в середине вертикальной стенки контура поперечного сечения имеют значения близкие к нулю.
Мето ди к а расчета напряженного состояния криволинейных тонкостенных стержней с деформируемым контуром
Одной из важнейших особенностей тонкостенных криволинейных стержней является искажение контура поперечного сечения. В случаях на-гружения криволинейного стержня сосредоточенной силой перпендикулярной плоскости кривизны (рис. 4.7) в произвольном его сечении деформацию контура возможно представить линейной зависимостью /69/: W=WX+WW, (4.3) где Wx - функция, определяющая деформацию контура при изгибе из плоскости кривизны; Wco- функция, определяющая деформацию контура при стесненном кручении. Поперечное сечение криволинейного стержня
Характер деформации контура при указанных воздействиях приведен нарис. 4.8. где Мх - изгибающий момент из плоскости кривизны; EL - бимомент; (4.4) у,ю - линейная и секториальная координаты произвольной точки сечения; Jx, J»- осевой и секториальный моменты инерции; Кх.Ксо- коэффициенты, характеризующие изменение нормальных напряжений в связи с искажением контура сечения.
Коэффициенты Кх, К» изменяются как вдоль оси стержня (координата z), так и вдоль серединной линии поперечного сечения полок (координата у). Е.А.Бейлиным /69/ приводится следующее выражение для коэффициентов: Ki(y, z) = 1 - f,(z)(l - К), і = х, со (4.5) Функция fi(z) характеризует переменность коэффициентов Ki(y,z) вдоль оси стержня. Ее значение может быть найдено решением соответствующего дифференциального уравнения четвертого порядка /70/. При равномерном искажении профиля вдоль оси стержня fi(z)=l. Там же /70/ приведены аналитические зависимости для нахождения К Р (последние ввиду их громоздкости в настоящем параграфе не приводятся), а также графики, позволяющие определять КР в зависимости от геометрических параметров сече ния:
Изложенная методика была использована для расчета напряженного состояния модели тонкостенного кривого бруса при пространственном на-гружении. На рис. 4.9 показана половина модели с нагрузкой Р перпендикулярной плоскости кривизны, а также построены эпюры изгибающего момента из плоскости кривизны и крутящего момента согласно выражений:
На рис. 4.10 приведена эпюра секториальной координаты со, согласно которой наибольшие напряжения от стесненного кручения возникают в угловых точках прямоугольного сечения.
Согласно упомянутой выше методике для всех сечений модели были подсчитаны силовые факторы и найдены коэффициенты Кх и К (табл. 4.1). Эпюра секториальной координаты со
Анализ напряжений, приведенных в табл. 4.2, показывает правомерность оценки напряженного состояния модели при изгибе из плоскости кривизны и при стесненном кручении по приводимой методике расчета. Наибольшие расчетные напряжения, определялись по предлагаемым аналитическим зависимостям отличались от экспериментальных на 9-14%. Минимальные напряжения вычислялись с несколько большей ошибкой (до 23% в отдельных сечениях). Нам представляется подобный результат удовлетворительным для практических инженерных расчетов узлов рам подвижного состава. Аналогичный результат получен при расчете напряжений во внешнем углу буксового проема боковой рамы тележки грузового вагона модели 18-755 при нагружении ее из плоскости кривизны, согласно схеме, приведенной на рис. 4.1. Расчетные напряжения по предлагаемой методике составили 183 МПа (по оценке С.М.Щудрака /74/ 201 МПа).
Все вышеотмеченное позволяет высказать рекомендации о правомерности и несомненной полезности использования теории Е.А.Бейлина-Э.Л.Аксельрада к оценке напряженного состояния узлов рам тележек подвижного состава при их пространственном нагружении.
Напряженное состояние несущей балки транспортера сцепного типа грузоподъемностью 340т
Буксовый проем боковой рамы тележки 546 (рис. 5.9) образован двумя сопряженными эксцентричными кривыми брусьями различных типов и имеет замкнутое прямоугольное тонкостенное поперечное сечение.
Для исследования напряженного состояния выбрано шесть ломаных равносторонних сечений боковой рамы. Сечение I и II относятся к эксцентричному кривому брусу, ограниченному дугами двух эксцентрично расположенных окружностей с радиусами R\ и R2. Остальные сечения (сечение III, IV, V, VI) относятся к эксцентричному кривому брусу, ограниченному сверху прямой линией и снизу дугой окружности Rj. Размеры всех расчетных сечений и величины внешней нагрузки даны в табл. 5.9.
Рис. 5.10 а - верхняя стенка; б - нижняя стенка. Коэффициенты постели каждого пролета с интенсивностью распределенной нагрузки неразрезной балки подсчитаны в соответствии с выше приводимыми рекомендациями в зависимостями от кривизны, длин и формы поперечного сечения каждого участка стенки. Обратим внимание, что на участке 2-3 (сечение III) поперечное сечение имеет форму швеллера. Расчеты показали, что коэффициенты упругого основания г и S, найденные для швеллерного и прямоугольного поперечных сечений, мало отличаются друг от друга, поэтому, на участках 2-3 верхней и нижней стенок рассматривается одно упругое основание.
Отметим также, что для нижней стенки выполнено искусственное разбиение участка 1-3 на два пролета 1-2 и 2-3 с одинаковым упругим основанием внешней нагрузкой. Это вызвано желанием обеспечить устойчивое решение в операциях над матрицами в предложенных программах. Исследования показали, что устойчивость решения наблюдается при соотношениях 1/т 3.
Для каждой стенки боковой рамы нагрузка и характеристики упругого основания на каждом участке неразрезной балки приведены в табл. 5.10.
Эпюры приведенных прогибов Wnp и коэффициентов использования сечений получены по предлагаемой в работе методике и изображены на рис. 5.10. С учетом этих данных вычислены наибольшие напряжения в крайних точках каждого сечения. Значения напряжений, а также основных параметров и геометрических характеристик для всех сечений даны в табл. 5.11.
Из всех рассмотренных сечений боковых рам тележек, три относились к левой половине буксового проема (сечения, проведенные под углом 9 = 0, 15, 30, см. рис. 5.5, 5.7, 5.9) и четыре к правой части (сечения 6 = 0, 15, 30, 45). В этих сечениях проводилось сравнение величин нормальных напряжений, возникающих в боковых рамах от вертикальной нагрузки. Все значения напряжений сведены в табл. 5.12.
Анализ табл. 5.12 и графиков рис. 5.11 показывает, что наиболее напряжена у боковин правая часть буксового проема. По уровню наибольших напряжений боковые рамы располагаются в следующем порядке: боковая рама тележки 100: сттах =11910 кН/м , боковая рама тележки 117: атах =94,9-10 кН/м , боковая рама тележки 546: сттах =80,1-10 кН/м .
С этих позиций геометрические размеры, конфигурация, форма сечений и другие конструктивные признаки боковой рамы 546 выглядят предпочтительнее других вариантов. Выполненные исследования, их анализ и выводы представлены Уральскому вагоностроительному заводу и несомненно будут способствовать проектированию наиболее удачного варианта буксового проема боковой рамы тележки грузового вагона.
Напряженное состояние несущей балки транспортера сцепного типа грузоподъемностью 340т
Для перевозки сверхтяжелых, имеющих большие размеры, грузов (мощных трансформаторов, реакторов, турбогенераторов, ракет) используются железнодорожные транспортеры. Существует целый ряд различных железнодорожных транспортеров /67/, отличающихся конструктивными особенностями, грузоподъемностью количеством осей. Одной из наиболее интересных моделей является двадцати четырехосный транспортер сцепного типа грузоподъемностью 340т (модель 14-6061) /67/, рис.5.12. Изменение наибольших напряжений по длине буксового проема в различных
Основным элементом транспортера является несущая балка (рис. 5.13), представляющая собой сложную конструкцию, состоящую из отдельных криволинейных и прямолинейных, сопряженных между собой участков. Подобная балка имеет ярко выраженное переменное по высоте тонкостенное поперечное сечение сложной формы. Исследования /68/ показали, что расчет напряженного состояния криволинейных участков несущих балок практически невозможен методами сопротивления материалов, основанных на гипотезе плоских сечений. Достоверную картину напряженного состояния можно получить на основе методов /68/, использующих гипотезу неплоских сечений и учитывающих деформацию контура тонкостенного сечения.
На рис. 5.13 указан ряд расчетных сечений несущей балки транспортера, в которых выполнялся расчет напряженного состояния. Сечения II, III, IV относятся к криволинейным участкам несущей балки различной конфигурации.
Сечение II - к участку, ограниченному дугами эксцентрично проведенных окружностей; сечение III - к участку, ограниченному снизу прямой линией, сверху дугой окружности; сечение IV - к участку, ограниченному снизу дугой окружности, сверху прямой линией. Все перечисленные участки представляют собой частные случаи различных эксцентричных кривых брусьев, расчет на изгиб которых подробно рассмотрен в /68/. Все криволинейные участки имеют переменную высоту сечений и, согласно /68/, расчетные сечения по участкам проведены как ломанные равносторонние.
Форма поперечных сечений балки приведена на рис. 5.14. Во всех случаях сечения состоят из четырех прямоугольных коробок с развитыми верхними и нижними стенками. Для сечения II имеется пластина, перекрывающая две смежные коробки. На рис. 5.14 указаны также места наклейки датчиков омического сопротивления при проведении натурных испытаний железнодорожного транспортера ОКБ Луганского производственного объединения тепловозостроения, выпускающим настоящие транспортеры.