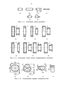Содержание к диссертации
Введение
Глава 1. Современное состояние проблемы контроля формы поверхностей качения подшипников 10
1.1. Типы асферических поверхностей качения прецизионных подшипников и требования к точности их формы 10
1.2. Существующие методы контроля поверхностей качения подшипников 16
Глава 2. Теоретические основы интерферометрического метода 40
2.1. Идея метода и оптические схемы измерительной ветви интерферометра 40
2.2. Определение оптимальных оптических схем объективов измерительной ветви 58
2.3. Методика дешифрирования интерференционных картин 76
2.4. Предельные возможности метода 99
Глава 3. Экспериментальное исследование метода 104
3.1. Лабораторный макет интерферометра 104
3.2. Подготовка эксперимента 110
3.3. Выполнение эксперимента и его результаты 115
Глава 4. Требования к оптическим и механическим узлам интерферометра 128
4.1. Требования к качеству изготовления основных оптических деталей 128
4.2. Оценка чувствительности измерительной ветви к погрешностям установки оптических элементов и требования к ее механическим узлам 135
4.3. Способы повышения контраста интерференционных картин и точности измерений 153
Заключение 158
Литература 159
- Существующие методы контроля поверхностей качения подшипников
- Определение оптимальных оптических схем объективов измерительной ветви
- Выполнение эксперимента и его результаты
- Оценка чувствительности измерительной ветви к погрешностям установки оптических элементов и требования к ее механическим узлам
Введение к работе
Подшипники качения нашли широчайшее применение в машиностроении и приборостроении благодаря малым потерям на трение, большой грузоподъемности, простоте монтажа, ухода и обслуживания. При их использовании хорошо выполняются условия взаимозаменяемости и унификации элементов узла; в случае выхода из строя подшипник легко может быть заменен новым, так как все его параметры стандартизированы. Все это обусловило массовый характер выпуска подшипников.
Высокие эксплуатационные свойства подшипников не могут быть достигнуты без получения точных поверхностей качения. Влияние качества дорожек качения (желобов) колец и механически сопряженных с ними поверхностей шариков или роликов на общую точность подшипника особенно велико, так как они, находясь во взаимном контакте, во многом определяют его кинематику. Искажение формы поверхностей качения, а также наличие на них отдельных дефектов ведет к появлению пространственных колебаний оси вращения, сокращению срока службы, усилению шума при работе, особенно на больших оборотах. Если отклонение от круглости шариков диаметром 8 мм возрастает с 0,125 мкм до 0,5 мкм, шум подшипника усиливается на 15 - 20 дБ. Это, например, совершенно недопустимо в механизмах подводных лодок.
Для выполнения жестких требований к качеству поверхностей необходим надежный контроль их формы. В настоящее время он основывается на применении сложных и весьма дорогих контактных устройств. В целом они обеспечивают приемлемые погрешности измерений, но их возможности уже
5 близки к своему пределу. Существующие измерительные приборы позволяют получить только набор сечений и не дают интегральной оценки формы поверхности. Сам процесс измерений является трудоемким и длительным.
В связи с этим понятен интерес к использованию для контроля поверхностей качения подшипников оптических методов, способных обеспечить выполнение жестких требований к правильности их формы. В настоящее время эти требования для прецизионных подшипников стали сопоставимыми с требованиями, предъявляемыми к поверхностям оптических деталей. Применение оптических методов становится возможным, так как малая шероховатость поверхностей качения (порядка 0,08 мкм) позволяет получить от них зеркальное отражение оптического излучения.
Анализ имеющихся литературных источников позволяет сделать вывод о перспективности использования для контроля поверхностей качения интерферометрических методов. Они обеспечивают как качественную оценку, так и количественные измерения погрешностей формы поверхности. Известные из немногочисленных опубликованных работ интерферометры предназначены для контроля сферических и торических поверхностей, характерных для шарикоподшипников. Их применение ограничивается рядом недостатков. Чаще всего — это невозможность контроля сразу всей поверхности или ориентированность на какой-то конкретный тип деталей. Для другой, весьма многочисленной группы подшипников качения — роликовых — пригодные к использованию методы фактически отсутствуют.
Исходя из этого автор поставил цель создать интерфе-рометрический метод, обеспечивающий полноценный качест-
6 венный и количественный контроль формы асферических поверхностей качения как шариковых, так и роликовых подшипников. Для достижения этой цели были решены следующие задачи:
1. Анализ номенклатуры выпускаемых подшипников и оп ределение типов асферических поверхностей качения. Систе матизация погрешностей формы данных поверхностей и выяв ление их характерных значений.
2. Разработка функционально связанных между собой схем измерительной ветви интерферометра, обеспечивающих интегральную оценку формы поверхностей качения. Создание методики расчета её конструктивных параметров.
Разработка методов дешифрирования интерференционных картин.
Исследование чувствительности измерительной ветви интерферометра к малым перемещениям оптических элементов или контролируемых деталей. Определение требований к её оптическим и механическим узлам.
Экспериментальное исследование метода.
Решение поставленных задач осуществлялось математическим моделированием с использованием теории интерферометров и теории аберраций оптических систем. При проведении исследований использовались пакеты прикладных программ «MapleV», «MathCad», «OPTIC» и «Призма».
Научная новизна работы заключается в следующем: 1. Предложен и обоснован новый интерферометрический метод контроля формы торических, цилиндрических, конических и бочкообразных поверхностей качения подшипников, основанный на применении оптических систем, строящих кольцевое изображение осевой предметной точки. Это позво-
7 ляет формировать измерительный пучок лучей, охватывающий одновременно всю контролируемую поверхность и при этом использовать известные двухлучевые схемы интерферометров.
2. Показано, что использование телескопической линзы в качестве коррекционного элемента позволяет значительно снизить остаточную сферическую аберрацию двузеркальных реверсивных объективов при высокой светосиле последних.
3. Разработана методика определения погрешностей формы цилиндрических и конических поверхностей по интер- ферограмме, полученной при автоколлимационно-реверсивном ходе лучей в измерительной ветви интерферометра и нерав ных углах падения лучей на контролируемую поверхность.
Практическая ценность работы заключается в том, что разработанный метод обеспечивает полноценный контроль формы асферических поверхностей качения и может быть использован в исследовательских целях для выявления причин возникновения погрешностей формы данных поверхностей, а также коррекции и совершенствования технологических процессов изготовления прецизионных подшипников. Полученные в ходе работы результаты позволяют:
Рассчитать универсальную измерительную ветвь интерферометра для контроля асферических поверхностей качения подшипников, полностью совместимую с серийными двух-лучевыми интерферометрами.
Для измерительной ветви интерферометра рассчитать конструктивно простой объектив с высокой степенью коррекции сферической аберрации, обладающий одновременно высокой светосилой и большим рабочим отрезком.
Определить допустимые погрешности юстировки измерительной ветви интерферометра и оценить её чувствитель-
8 ность к малым перемещениям оптических элементов, включая контролируемые детали.
Минимизировать влияние факторов, снижающих контраст интерференционных картин.
Определить по интерферограммам реальные значения погрешностей формы контролируемой поверхности качения с учетом особенностей хода лучей в измерительной ветви интерферометра и дать заключение о ее качестве.
На защиту выносятся следующие основные положения:
1. Разработанный интерферометрический метод обеспе чивает качественный и количественный контроль формы асфе рических поверхностей качения подшипников в широком раз мерном диапазоне с получением интегральной оценки формы поверхности.
Методика выбора и расчета объективов измерительной ветви интерферометра обеспечивает получение оптических схем объективов, сочетающих необходимое относительное отверстие и большой рабочий отрезок с высоким уровнем аберрационной коррекции.
Методика дешифрирования интерференционных картин позволяет определять нормируемые погрешности формы поверхностей качения даже при неравенстве углов падения лучей на контролируемую поверхность и автоколлимационно-реверсивном ходе лучей в измерительной ветви.
Требования к точности установки основных оптических элементов, определенные на основе анализа оптических свойств измерительной ветви интерферометра, практически всегда выполнимы.
Апробация работы.
Материалы диссертации обсуждались на научных семина-
9 pax кафедры «Оптико-электронные приборы научных исследований» (РЛЗ) МГТУ им. Н.Э. Баумана, были доложены на международной конференции «Прикладная оптика — 98» (г. Санкт-Петербург) и отражены в трех публикациях (статья и тезисы докладов на двух конференциях). Кроме того, при определении оптимальных оптических схем объектива измерительной ветви интерферометра использованы материалы статьи автора, посвященной расчету асферического зеркала для формирования параболического волнового фронта (принята к публикации в журнале «Вестник МГТУ, серии «Приборостроение», №3, 2000 г., справка № ИРЖ-9 от 25.01.2000 г.).
Существующие методы контроля поверхностей качения подшипников
По способу обнаружения погрешностей формы контролируемых деталей все контрольно-измерительные средства можно разделить на механические (электромеханические), реализующие контактные методы измерений, и оптические (оптико-электронные) , являющиеся, за редким исключением, бесконтактными .
В настоящее время производственный контроль формы поверхностей качения подшипников базируется на применении контактных устройств — щуповых приборов, основанных на стрелочных индикаторах, кругломерах и профилографах (про-филометрах).
Контроль при помощи стрелочных индикаторов является самым простым и потому весьма распространенным. Овальность и четная огранка детали (Д) могут быть измерены двухконтактными приборами (рис.1.4 а). Огранка с нечетным числом граней такими приборами не обнаруживаются. Ее можно измерить в кольце (рис.1.4 б) или трехконтактными измерительными устройствами, например на призме (рис.1.4 в). При измерении в кольце за величину огранки принимают разность наибольшего и наименьшего показаний индикатора, при измерениях на призме — аналогичную величину, умноженную на коэффициент, зависящий от числа граней и угла призмы [ б]. Схемы рис.1.4 а-в характерны для тел качения. Способы базирования подшипниковых колец регламентированы ГОСТ 520-89 [5].
Для воспрогизведения реального профиля детали служат кругломеры с вращающимся наконечником или деталью (рис.1.4 г). Наконечник преобразователя совершает радиальные колебания, соответствующие изменению радиуса детали. Перемещения наконечника преобразуются в круглограмму детали с коэффициентом увеличения 50-200000 раз. Отклонение от круглости определяется по отклонению круглограммы от базовой окружности, радиус которой находится расчетным путем [б]. Погрешность измерения составляет, согласно ГОСТ 17353-89, 10-15% в зависимости от класса точности прибора [7].
Принцип действия профилографа основан на ощупывании исследуемой поверхности алмазной иглой с радиусом закругления 10 мкм, пространственные колебания которой преобразуются в соответствующие изменения напряжения (рис.1.4 д). Измерительный сигнал формируется за счет изменения индуктивности катушек преобразователя при колебаниях воздушного зазора между сердечником и якорем, на котором закреплена игла [б]. Погрешность измерения отклонений формы поверхности при помощи профилографов составляет 0,08...0,8 мкм, что в целом позволяет обеспечить контроль колец и тел качения большинства подшипников. С использованием в качестве чувствительного элемента алмазной иглы или тонкого наконечника связаны основные недостатки контактных методов. Во-первых, щуповые приборы обеспечивают за один прием контроль лишь узкого участка желоба или тела качения. Для получения информации обо всей поверхности необходимо измерение множества сечений. Этим объясняется высокая трудоемкость контактных методов. В конечном итоге оценка реальной формы поверхности качения неизбежно носит дискретный характер. Отсутствие интегральной оценки формы контролируемой поверхности усложняет подготовку или коррекцию технологических процессов. Во-вторых, к настоящему времени возможности совершенствования щуповых устройств приблизились к своему пределу. Дальнейшее повышение точности щуповых приборов сопряжено с их удорожанием и значительным усложнением конструкции. В-третьих, согласно ГОСТ 17353-89, установленная безотказная наработка кругломеров и профилографов составляет лишь 3000 измерений при средней наработке до полного отказа в 17500 измерений. Эти данные свидетельствуют о недостаточной надежности контактных устройств и их высокой подверженности износу. Указанные недостатки заставляют обратиться к бесконтактным оптическим методам контроля. С учетом принципов регистрации отклонений формы поверхности их можно распределить по следующим группам: - методы оптико-электронного сканирования/ - методы контроля по виду дифракционного кольцевого изображения; - автоколлимационные методы; - интерференционные методы. В основу оптико-электронных сканирующих методов и устройств положен принцип получения информации об объекте путем фотоэлектрического анализа изображения тест-объекта, сформированного пучком, при помощи которого последовательно «просматриваются» различные участки проверяемой поверхности. Эти устройства, в отличие от щуповых приборов, являются двухканальными, состоящими из проецирующей и регистрирующей систем. В качестве примера на рис.1.5 а показан прибор, построенный на базе двойного микроскопа с совмещенными предметными плоскостями [8] . В нем функцию анализа изображения тест-объекта (диафрагма с малым отверстием) выполняет щель, перемещаемая в плоскости рисунка перпендикулярно оптической оси микроскопа при помощи механизма, связанного с электромагнитным или пьезоэлектрическим преобразователем. Принцип действия измерительного устройства понятен из рис.1.5 б. Изображение тест-объекта S находится на контролируемой поверхности Р в положении Si , а в плоскости щелевой диафрагмы анализатора — в положении Si". Сканирование контролируемой поверхности осуществляется ее перемещением вдоль образующей или вращением вокруг оси симметрии. Если при этом высота профиля поверхности изменилась на величину h, то изображение сместиться в положение S2r, а в плоскости диафрагмы анализатора — в положение S2". Расстояние S!"S2" служит мерой отклонения профиля поверхности. Оно измеряется по величине напряжения, подаваемого на преобразователь и необходимого для смещения щели из положения Si" в положение S2". Диапазон измерений определяется глубиной резкости изображения микроскопа и зависит от апертуры его объектива. Например, по данным [8], для объектива с фокусным расстоянием 13,9 мм и апертурой 0,3 диапазон составляет 50 мкм. Порог чувствительности не превышает 0,05 мкм, что в сочетании с малошумящим электронным трактом обеспечивает получение более высокой точности по сравнению с точностью щуповых приборов.
Определение оптимальных оптических схем объективов измерительной ветви
Достоверность результатов измерений и предельные размеры контролируемых поверхностей качения в значительной степени определяются объективами, которыми комплектуется измерительная ветвь интерферометра. Именно от их качества зависит, насколько «идеальным» может считаться волновой фронт пучка, направляемого на контролируемую поверхность. Поэтому к объективам приходится предъявлять жесткие требования .
Размер захватываемого световым пучком фрагмента контролируемой поверхности зависит от угла сходимости пучка со (рис.2.2-2.5) . Чем выше апертурный угол объектива, тем большую ширину имеет интерференционное поле и тем легче проводить обработку интерферограмм. Поэтому применяемый объектив должен обладать возможно большей светосилой. Анализ геометрических параметров поверхностей качения и схем рис.2.2-2.5 показывает, что речь идет об относительных отверстиях (D/f), равных 1:1,5 — 1:0,8 и более. Свободный отрезок объектива должен быть достаточным для размещения всех элементов измерительной ветви или же для обеспечения ее фокусировки при контроле колец, диаметр которых может составлять сотни миллиметров.
Поскольку в предлагаемом методе измерительный пучок формируется оптическими элементами, установленными по ходу лучей после объектива, аберрации последнего для вне-осевых точек пространства предметов могут иметь любые значения. Однако ввиду двойного прохождения пучка через объектив вопросам коррекции его сферической аберрации должно быть уделено самое пристальное внимание. Сопоставляя требования к точности формы поверхностей качения различных подшипников, можно заключить, что для контроля большинства из них достаточно иметь объективы, у которых остаточная сферическая аберрация, выраженная в волновой мере, составляет %/б — Х/4, то есть, соответствует уровню критерия Рэлея {X — длина волны излучения). При контроле поверхностей качения особо ответственных подшипников небольшого диаметра желательно использовать объективы с остаточной аберрацией А,/10 — Х/8. Тогда они могут считаться идеальными, а влияние их собственных аберраций на форму волнового фронта не учитываться. И хотя эти требования несколько ниже предъявляемых при контроле оптических поверхностей, высокие относительные отверстия делают задачу аберрационной коррекции объективов весьма сложной.
Так как предлагаемый метод подразумевает использование лазера в качестве источника излучения, то необходимости в ахроматизации объективов измерительной ветви не возникает.
Очевидно, что большой (сотни миллиметров) свободный отрезок объектива при высокой светосиле неизбежно приведет к значительным световым диаметрам его оптических деталей и узлов. В этих условиях применение сложных многокомпонентных систем не гарантирует соответствия реальных аберраций расчетным значениям и их неизменность с течением времени; изготовление таких объективов сопряжено с технологическими трудностями. Поэтому конструкция объектива должна быть предельно простой. Указанные требования к объективу ставят его в ряд наиболее ответственных элементов измерительной ветви интерферометра.
Именно малый свободный отрезок и конструктивная сложность, быстро возрастающая с увеличением светосилы, являются основными причинами непригодности для нашего метода линзовых объективов. Например, при относительном отверстии 1:0,75 число линз объектива достигает 9 [22]. Немаловажно и то, что большое количество линз приводит к большим световым потерям. Это неприемлемо ввиду малых коэффициентов отражения от контролируемых поверхностей стальных деталей. Поэтому поиск оптимальных оптических схем объективов для измерительной ветви следует проводить среди зеркальных или зеркально-линзовых систем.
Конструктивное исполнение объективов может быть различным. Предлагаемые здесь решения являются наиболее рациональными с точки зрения автора. Для их реализации не требуется каких-то принципиально новых конструкторских и технологических решений. Если диаметр кольцевого изображения АА., формируемого в измерительной ветви, превышает диаметр входящего в него пучка, то в роли объектива может выступать одиночное зеркало (рис.2.7). Наилучшим объективом для таких схем является параболическое зеркало, полностью свободное от сферической аберрации. Однако его применение сдерживается трудностями изготовления и контроля. Отметим, что контроль высокоапертурных параболических поверхностей компенсационным методом может потребовать применение асферических поверхностей в самом компенсаторе для упрощения его конструкции и повышения надежности. Все это сводит на нет преимущества парболического зеркала, предоставляемые его коррекционными возможностями.
Выполнение эксперимента и его результаты
Подготовленный эксперимент позволил получить рабочую интерференционную картину и сделать ряд важных наблюдений, позволяющих избежать ошибок при практической реализации предлагаемого метода.
В ходе эксперимента были определены способы контроля правильности установки конической или цилиндрической отражающей поверхности в сходящийся пучок лучей. В лабораторном макете процесс установки контролировался по фигурам, наблюдавшимся на экране в фокальной плоскости коллиматора . Покажем, как по их виду можно оценить положение поверхности ролика или зеркала и направление необходимых юстировочных подвижек. Для этого исследуем, как меняется форма кольцевого изображения при поперечном смещении ролика. Принципиальной разницы между цилиндрической и конической поверхностью нет. Форма кольцевого изображения меняется одинаково. Разница лишь в том, что в первом случае оно остается в той же плоскости, а во втором — лежит на конусе с углом при вершине 180 —2#, проходящем через исходное кольцевое изображение. Поскольку нас интересует только форма изображения без учета дефокусировки, рассмотрим для простоты цилиндрическую поверхность. На рис. 3.4 приведено сечение измерительной ветви со стороны объектива, перпендикулярное к его оптической оси и проходящее через ролик радиусом гр. Центр С сечения ролика смещен относительно фокуса объектива F на величину е. Точка А кольцевого изображения является изображением точки F в плоском зеркале, совпадающем с касательной, проходящей через точку М падения луча.
Примем прямую, содержащую отрезок CF , за полярную ось, а фокус объектива F — за полюс. Тогда (р — полярный угол падающего луча, р , р — полярный угол и радиус-вектор точки А кольцевого изображения. Наша задача — получить уравнение кольцевого изображения при смещенном ролике
Если h — высота текущего сегмента ролика, то справедливы следующие соотношения: Кроме того, из геометрических соображений для полярного угла (р падающего в точку М луча и угла падения і можно записать следующие выражения:
Так как отрезки СМ и F A параллельны, то p = 2A4AcOSi или же, с учетом (3.1) и (3.3): Из соотношений рис.3.4, учитывая (3.2) и (3.3), получаем: Пусть е/гр=у. Используя известные тригонометрические соотношения, из (3.5) получаем формулу, выражающую ф че Раскрывая косинус разности в выражении (3.4) и подставляя в него (3.7) и (3.8), получаем искомое уравнение, описывающее кольцевое изображение АА при смещенном ролике:
Из уравнения (3.9) становится понятным поведение кольцевого изображения при различных положениях ролика. Если у 1, то оно принимает форму рис.3.5 а — грубая установка ролика; при у=1 — изображение превращается в кардиоиду (рис.3.5 б). При дальнейшем снижении децентрировок ролика (0 у 1) перегиб кольцевого изображения исчезает, и по мере приближения контролируемой поверхности к правильному положению оно становится все ближе к правильной окружности (рис.3.5 виг). Сравнение рис.3.4 и 3.5 показывает, что ось симметрии получающихся фигур соответствует положению плоскости смещения ролика или конического зеркала, а положения перегибов (петель) - направлению смещения. Именно это и наблюдалось во время эксперимента при установке ролика.
Нарушения осевой симметрии измерительной ветви могут быть обнаружены по интерферограмме. Смещения оптических элементов относительно оси пучка при контроле конических поверхностей приводит не только к дополнительному искривлению полос, но и к изменению их направления на различных участках картины. Указанный эффект хорошо просматривается на интерферограмме (рис.3.б). Это можно объяснить следующим образом.
Если поверхность качения имеет коническую форму, то при ее децентрировке каждая точка кольцевого изображения формируется лучами, не лежащими в одном меридиональном сечении, что ведет к перераспределению деформаций по волновой поверхности. Исключение составляют только лучи, падающие на коническую поверхность в плоскости ее смещения. Поведение лучей в остальных сечениях становится понятным из рис.3.7, где показан конический ролик со стороны малого торца, сдвинутый на величину е относительно оптической оси объектива с фокусом F .
Выберем для рассмотрения произвольный фрагмент пучка. Из схемы рис.3.7 видно, что после отражения в одной плоскости лежат лучи, падающие на коническую поверхность по линии МіМ2 в наклонном сечении. Данные сечения имеют криволинейный профиль. Следствием этого является дополнительное искривление волновой поверхности по направлению 1-2 (цифрами обозначены крайние лучи рассматриваемого фрагмента).
Оценка чувствительности измерительной ветви к погрешностям установки оптических элементов и требования к ее механическим узлам
Деформация волнового фронта, идущего из измерительной ветви, есть результат суммарного влияния погрешностей контролируемой поверхности и ошибок юстировки. Данные ошибки связаны с децентрировками элементов измерительной ветви и с появлением в ней продольных дефокусировок. Если децентрировки обнаруживаются по нарушению симметричности интерференционной картины и в принципе могут быть устранены в процессе юстировки, то дефокусировки сохраняют симметричность интерферограммы и не могут быть учтены непосредственно. Поэтому возникает вопрос: насколько точно нужно устанавливать оптические элементы измерительной ветви для надежного контроля поверхности качения, и какой чувствительностью должны обладать предназначенные для этого котировочные механизмы? Очевидно, что исследование всех схем измерительной ветви с полным учетом всех возможных комбинаций погрешностей — задача крайне сложная. Поэтому при определении требований к механическим узлам в первую очередь необходимо выделять и анализировать поведение элементов, характерных для абсолютного большинства схем.
Сравнивая влияние наклона на величину Ла конического зеркала или ролика с влиянием погрешности его угла Ла, убеждаемся, что механизмы возникновения дефокусировок при наличии данных погрешностей являются аналогичными. В обоих случаях изменяется высота Н и происходит продольное смещение кольцевого изображения. В результате оно «уходит» с поверхности сферического зеркала (рис.2.2 а и 2.3 а) или перестает совпадать с центрами кривизны профиля контролируемой торической поверхности. При перекосе зеркальной конической поверхности наибольшие дефокусировки будут иметь место в плоскости децентрировки. При одинаковой абсолютной величине в обоих полуплоскостях они будут отличаться по знаку, следствием чего и является нарушение симметрии интерференционных колец. Здесь предполагается, что поворот детали на угол Ла происходит относительно заднего торца — наиболее удобного места для ее крепления (рис.4.2). При отклонении угла конуса от номинального значения дефокусировка оказывается одинаковой по величине и знаку во всех меридиональных сечениях. Рассматривая перекос ролика в плоскости децентрировки, можно принять, что в разных полуплоскостях его образующие
приобрели погрешность угла конуса ±Ла. Эта значит, что одна и та же формула, связывающая модуль дефокусировки Л/ с величиной Ла, может быть использована как для назначения требований к котировочным механизмам, устанавливающим в правильное положение ролик (зеркало), так и для вычисления отклонения угла конуса от номинала, измеряемого по образцовой детали (схема рис.2.2 а). Величину Af необходимо определять вдоль радиуса сферического зеркала или дуги желоба, являющегося нормалью к поверхности. Так как реальные значения Ла малы, то погрешности, связанные с нарушением симметричности фрагментов отраженного пучка относительно центральных лучей, можно не учитывать. Из рис.4.2 видно, что если положение сферического зеркала остается неизменным, то величина дефокусировки
Входящие в формулу (4.8) Н и Rz являются по сути координатами точки Аг смещенного кольцевого изображения в системе координат с началом в центре кривизны сферического зеркала. Угол Q соответствует наклону центрального луча в идеально отъюстированной измерительной ветви, то есть
Входящая в (4.9) составляющая Az варьируется в зависимости от величины и знака Ла и может быть определена как приращение проекции на оптическую ось любого из лучей пучка на участке между точкой отражения от поверхности ролика и точкой изображения. Для определенности возьмем крайний верхний луч пучка, угол наклона ст3 которого определяется светосилой объектива. Тогда с учетом закона отражения проекция участка DA (рис.4.2) рассматриваемого луча на оптическую ось равна Искомое приращение Az определяется путем дифференцирования выражения (4.11) по углу а: