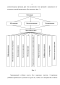
Содержание к диссертации
Введение
Глава 1. Методические основы создания учебника и учебно методического комплекса по математике для
1.1. Структурирование и создание учебников и учебно-методических комплексов по математике для общеобразовательных школ 10 - 32
1.2. Методические особенности определения основных содержательных линий школьного курса математики
1.3. Разработка общеобразовательных учебных программ по математике для основной и старшей школ на основе принципа преемственности обучения 49 - 55
Выводы по Главе 1 56 - 57
Глава 2. Методика организации обучения математике в
2.1. Особенности организации обучения математике в 5-9 классах 58 - 79
2.2. Особенности организации обучения математике в 10-11
2.3. Экспериментальная работа по организации обучения математике по учебникам и УМК для 5-11 классов 87 - 122
Выводы по Главе 2 123
Заключение 124 - 125
Список литературы
- Методические особенности определения основных содержательных линий школьного курса математики
- Разработка общеобразовательных учебных программ по математике для основной и старшей школ на основе принципа преемственности обучения
- Особенности организации обучения математике в 10-11
- Экспериментальная работа по организации обучения математике по учебникам и УМК для 5-11 классов
Методические особенности определения основных содержательных линий школьного курса математики
Структурные единицы учебника - главы и параграфы. Материалы главы и параграфа являются тематически завершенными, сюжетно целостными; а также их содержание и объем соответствуют возрастным особенностям учащихся.
При создании ряда учебников по математике для казахстанских школ авторы (Математика - 5-6, авторы: А.Е.Абылкасымова, Т.П.Кучер, З.А.Жумагулова; Алгебра - 7-9, Алгебра и начала анализа - 10-11, авторы: А.Е.Абылкасымова, З.А.Жумагу лова, В.Е.Корчевский и др.) стремились обеспечить возможность организации самостоятельного овладения учащимися математическими знаниями, т.е. условий для самообразования [9-17].
Основные положения концепции учебников авторского коллектива: сочетание в учебнике научности и доступности изложения текстов, использование наглядности; ориентация содержания учебного материала на фундаментальные знания, снижение информационной перегрузки; продолжение формирования математических понятий, в условиях, которые обеспечивают преемственность и перспективность образования; реализация в учебнике дидактических принципов последовательности и систематичности, единства обучения и воспитания; обеспечение условий для лучшего осмысления изучаемого материала через постановку проблем, возможности использования как активных форм обучения, так и пассивных в определённых условиях; создание условий для организации самостоятельной познавательной деятельности учащихся, умений применять полученные знания на практике; ориентация на применение современных (в том числе информационно-коммуникационных технологий) педагогических технологий, побуждающих у учащихся интерес и желание учиться; обеспечение различной глубины изучения материала через систему заданий разных уровней сложности, развитие творческого мышления учащихся в том числе с использованием дивергентных задач; развитие интеллектуального уровня на основе общечеловеческих ценностей и лучших традиций национальной культуры, обогащение социально-нравственного опыта, расширения представлений об окружающем мире; в учебниках сохранена традиционная для отечественного образования фундаментальность изложения теории, формирования умений и навыков. Изложение материала осуществляется кратко, глубоко, экономно и строго, раскрывая его сущность через постановку проблем и их решение и демонстрируя применение теории на примерах; важное внимание уделяется осознанности усвоения теории благодаря вплетению нового материала в известный, постановке проблем, требований объяснить полученные результаты при изложении теоретического материала; материал учебников изложен с учетом возрастных особенностей учащихся, в частности, уровнем развития их мышления. Овладение новым материалом осуществляется на основе организации деятельности учащихся с помощью системы упражнений и привлечением наглядности, которые подведут учащихся к открытию новых для них знаний, самостоятельной формулировке выводов, правил, алгоритмов; усилена коммуникативная направленность изложения учебного материала, созданы предпосылки для формирования теоретического мышления, разработаны упражнения для организации совместной деятельности учащихся по открытию новых для них знаний для групповой, индивидуальной и самостоятельной работы.
Надо отметить, что особое значение для авторов учебников имело психоэмоциональная составляющая обучающихся, а именно, для какого уровня образования создавался тот или иной учебник. Так, например, «переход из начального уровня школьного образования в основной средний уровень для учащихся является весьма сложным процессом, который сопровождается повышенным уровнем эмоциональности, вызывает у них тревогу. Поначалу многие даже способные дети с трудом перестраиваются на новую для них систему обучения. Поэтому в начале 5 класса содержание материала нами было направлено на систематизацию знаний и сформированных математических умений в 1-4 классах и на их углубление. Тем самым была обеспечена преемственность в обучении учащихся математике на начальном и основном уровнях среднего образования.
Структура учебников математики начальных классов и 5-6 классов существенно отличаются. Учебник начальных классов строится поурочно и материал излагается по концентрам (концентрическое изложение материала). Основное содержание каждого урока - это упражнения по формированию математических умений и навыков. Для формирования новых математических знаний младших школьников используются иллюстрации, объяснительные тексты отсутствуют. В то время, как учебник математики для 5 класса основного уровня среднего образования помимо упражнений содержит объяснительные тексты, в которых дается изложение теоретического материала. Особенностью составления учебника по математике для 5 класса является изложение материала на индуктивной основе, с использованием конкретных примеров. Так, первый раздел учебника «Натуральные числа и нуль» содержит не только упражнения, но и обобщенный теоретический материал, изученный в курсе математики начальных классов школы, и включает элементы нового. Рассмотрим это на примере нескольких тем:
1) «Сравнение натуральных чисел» - в начальных классах учащиеся научились сравнивать натуральные числа по их записи и на основе порядка при счете. При изучении данной темы дети учатся сравнивать натуральные числа на основе расположения чисел на координатном луче;
2) «Сложение натуральных чисел» - свойства сложения были изучены учащимися в начальных классах. А новым для детей является обоснование изученных свойств с помощью координатного луча;
3) «Текстовые задачи» - новым в данной теме является то, что учащиеся рассматривают текстовые задачи, в которых за неизвестное необязательно должно быть принято то, что требуется найти в задаче. В этом случае после решения уравнения ответ задачи можно получить, выполнив действия, связывающие корень уравнения и искомое в задаче;
4) «Угол» при изучении данной темы идет актуализация знаний об углах, их видах и обозначениях. А новым для учащихся является ознакомление с термином «градус», формирование умений строить и измерять углы с помощью транспортира.
Для обеспечения преемственности при создании учебника по математике для 6 класса мы сохранили такую же структуру построения учебника, как и в 5 классе. Объяснительные тексты, как и в пятом классе, раскрывают теоретические сведения с помощью примеров. Пояснительный текст учебника построен на известных учащимся знаниях, приведенные рассуждения в процессе изложения нового материала настраивают учащихся на творческую, мыслительную деятельность» [46].
Разработка общеобразовательных учебных программ по математике для основной и старшей школ на основе принципа преемственности обучения
В многонациональном Казахстане целью общеобразовательной школы является воспитание общей культуры личностей, обучающихся путем соединения национальных и общечеловеческих духовных ценностей, создание благоприятных условий для разностороннего развития личности. Поэтому нами наряду с содержанием образования пересмотрены формы, методы и средства обучения на основе единства национальных, мировых, духовных, культурных ценностей в соответствии с современным уровнем развития науки, научно-технического прогресса Это, в свою очередь, предполагало создание казахстанских учебников и других учебно-методических пособий нового поколения. Так как в 90-е годы прошлого века учебники математики в основном были переводные (с русского на казахский), при этом не учитывались особенности родного языка, растительного и животного мира, социально-исторические, а также географические особенности республики. Например, названия некоторых населенных пунктов, растений, фамилии, имена и т.д., которые редко употребляются в национальных языках, тексты задач не были обогащены краеведческими материалами и т.д. Все это снижало воспитательную возможность учебника математики.
Исследования Д. Икрамова показали, что объем почти всех переведенных учебников превышает объем учебников-оригиналов, вследствие указанных выше недостатков [55]. Учет этих недостатков позволил усилить интерес к математике, так как задачи, построенные на региональном, местном материале содействуют осуществлению принципа воспитывающего обучения, приобщает детей к интересам, которыми живет окружающее их взрослое население страны. Включение национального материала: познание своей культуры, познание и понимание других культур, воспитание чувства национального достоинства и уважения к другим нациям и культурам, позволили расширить возможности математики. Например, при введении понятия геометрической прогрессии в учебнике «Алгебра» - 9 класс, мы приводим пример из национальной игры (отдаленно напоминающей шахматы) «Тогыз кріалак;» («Девять камушков»). Кроме того, при написании исторических данных мы включали сведения о трудах среднеазиатских ученых, об их вкладе в развитие математической науки [13].
Одним из принципов построения базового курса математики, в соответствии с нашей методикой, на основе выявленных основных принципов отбора учебного материала является ориентация на развитие личности учащегося.
Возникает вопрос, как необходимо построить содержание учебника по математике, чтобы обучение математике привело к развитию личности. Для этого мы обратились к одному из принципов теории развивающего обучения, разработанных Л.В.Занковым, о том, что процесс учения должен быть осознан обучающимися [52].
Говоря о развитии мышления обучающихся в процессе обучения математике, мы подразумеваем под этим - дифференцированный подход к обучению. В разработанных нами учебно-методических комплексах по математике, особенно в дидактических материалах и сборниках задач, это проявляется в том, что в них предлагаются системы упражнений разных уровней. Кроме того, в 10-11 классах идет дифференцированное обучение по двум направлениям: общественно-гуманитарному и естественно-математическому. Содержание базового курса математики является дифференцированным для обучающихся 10-11 классов. Поэтому в учебнике «Алгебра и начала анализа» для общественно-гуманитарного направления упражнения каждого параграфа разделены на две группы [15, 17]: А - обязательные задания для всех учащихся; В - задания определенной сложности, носящие поисковый характер. В отличие от учебника «Алгебра и начала анализа» для общественно-гуманитарного направления в учебнике «Алгебра и начала анализа» для естественно-математического направления упражнения каждого параграфа разделены на три группы [14, 16]: А - обязательные задания для всех учащихся; В - задания средней сложности; С - задания повышенной трудности, носящие поисковый характер. Учебники ориентирует учащихся на фундаментальные знания, формирует интеллектуальные и практические умения и навыки, создает основу для организации самостоятельного получения знаний, развития творческого, обеспечивает дифференцированный и индивидуальный подход.
Предусмотренные в учебниках задания разноуровневого характера (группы А, В, С) позволяют учителю создавать на уроке проблемные ситуации, развивать творческий потенциал учащихся, развивать критическое мышление. Имеется возможность и организации групповой формы работы учащихся, создания коллаборативной среды обучения. Ученик может переходить от ученического уровня усвоения знаний и приобретения навыков и умений к алгоритмическому, а затем к эвристическому и творческому. Следовательно, учитель имеет возможность организовать обучение учащегося по его индивидуальной траектории.
Тем самым, в этих учебниках упражнения направлены на развитие математических способностей учащихся и их интереса к математике. Такая дифференциация для учащегося дает определенное направление на организацию самостоятельной учебно-познавательной деятельности.
Влияние учебного материала, как и всякого другого материала, на мышление, умственное развитие многообразно. Развитие учащегося определяется совершенствованием содержания обучения, введением новых тем, в связи с социальным заказом общества, использованием различных дидактических средств и прежде всего решением задач.
Особенности организации обучения математике в 10-11
На уровне общего среднего образования вводятся систематические курсы «Алгебра и начала анализа» и «Геометрия». Как было сказано выше, обучение математике на данном уровне ведется по двум направлениям: естественно-математическому и общественно-гуманитарному. Отбор содержания курса алгебры и начала анализа для каждого направления определены типовыми учебными программами. В разделе 1.2 данной работы рассматривается различие отбора учебного материала по алгебре и началам анализа в 11 классе для обеих направлений. Для организации учебного процесса в 10-11 классах, используются учебники отдельно для каждого направления. При разработке учебников и учебно-методических комплексов для 10-11 классов нами учитывались и особенности изучения курса математики в данных классах.
Содержание курса математики для изучения в классах общественно-гуманитарного направления ориентировано на общекультурное развитие, формирование таких математических знаний и умений, которые нужны современному человеку для полноценной деятельности Особенность курса математики общественно-гуманитарного направления - снижение нагрузки за счет уменьшения числа строгих доказательств теорем при этом объяснения проводятся с опорой на наглядность и примеры. Таким образом овладение математическими знаниями осуществляется чаще всего на уровне ознакомления, без доказательств [79].
Важное место отводится использованию исторических сведений, в классах, где изучение языков осуществляется углубленно особое внимание надо уделить вопросам возникновения математических символов и терминов.
Содержание курса математики естественно-математического направления ориентировано на формирования у учащихся целостной картины окружающего мира, общенаучных умений, на развитие математических способностей, обеспечение сформированное умений для дальнейшего изучения реальных процессов и явлений, и решения прикладных задач.
Для организации самостоятельной работы учащихся с текстом, Ю.К. Бабанский предложил включить в содержание учебника текст, «который заранее может ориентировать учеников на самостоятельное изучение отдельных текстов без объяснения их учителем на уроках. К этим текстам будут предусмотрены определенные указания по самостоятельному изучению материала, образцы, планы работы» [27].
В объяснительном тексте темы «Производные тригонометрических функций» в учебнике «Алгебра и начала анализа» естественно-математического направления (10 класс) даны следующие задания для самостоятельного выполнения учащихся:
1. Используя формулу приведения и формулу нахождения производной сложной функции, докажите самостоятельно формулу (cosx) = -sinx. 2. Используя формулу tgx sin x cos x и формулу нахождения производной частного, докажите самостоятельно формулу (tgx) = cos2x [14].
Для самостоятельного выполнения учащихся тексте темы «Логарифм числа Основное лограифмическое тождество. Свойства логарифмов» в учебнике «Алгебра и начала анализа» естественно-математического направления (11 класс) даны следующие задания:
1. Самостоятельно напишите формулу перехода от натурального логарифма числа N к десятичному логарифму этого же числа.
2. Самостоятельно составьте алгоритм решения неравенств, содержащих переменные под знаком модуля. Это задание вы можете выполнить, используя алгортим решения уравнений, содержащих переменные под знаком модуля [16].
В.КДайнеко считает, что «для всех учебников по предметам естественнонаучного цикла необходимо принять систему изложения «в трех уровнях» (выделение в учебниках совершенно обязательного, обязательного и необязательного материала), что будет способствовать решению проблемы разгрузки учебников. Первый уровень - наиболее важные определения и самое главное в каждой теме, без чего понимание остального материала невозможно; второй уровень - основной по объему материал, обязательный (в совокупности с первым уровнем) для всех учащихся; третий уровень - дополнительный материал, на данном этапе обучения для всех необязательный, но помогающий лучше понять основные закономерности или расширяющий кругозор учащегося» [41].
Так, например, в 10 классе при изучении темы «Способы решения тригонометрических уравнений и их систем», в учебнике общественно-гуманитарного направления рассматриваются - тригонометрические уравнения, которые сводятся к алгебраическим уравнениям; решаемые путем преобразований тригонометрическими формулами и путем понижения степени уравнения; однородные тригонометрические уравнения; в естественно-математическом направлений дополнительно рассматриваются уравнения, решаемые путем введения дополнительного угла. А при изучении темы связанной с применением производной для исследования функции, учащиеся естественно-математического направления находят асимптоты и множество значений функции.
Как было сказано ранее, система упражнений по каждой теме в учебнике общественно-гуманитарного направления состоит из двух групп (обязательные задания и задания средней сложности), а в учебнике для естественно-математического направления - из трех групп (обязательные задания, задания средней сложности и задания повышенной трудности).
Приведем примеры системы упражнений темы «Решение показательных неравенств и их систем» из учебников «Алгебра и начала анализа» для 11 классов по общественно-гуманитарному (ОГН) и естественно-математическому (ЕМН) направлениям (таблица 21) [16, 17].
Экспериментальная работа по организации обучения математике по учебникам и УМК для 5-11 классов
Данные таблиц 30-31 позволяют сделать первичное заключение об определенных преимуществах эффективности экспериментальной методики. Кроме этого, приведенные оценки говорят о несколько более высоком уровне усвоения учебного материала и по классам и по направлениям. Мы видим, что учащиеся 11 классов показали более полные и прочные знания, чем десятиклассники, а также, что учащиеся, обучающиеся на естественно-математическом направлении, усваивают учебный материал на более высоком уровне.
Таким образом, экспериментальное исследование о степени влияния предложенной нами структурной особенности разработки учебников и учебно-методических комплексов и внедрения его в практику обучения подтвердили наше предположение о том, что целенаправленное создание и использование учебников и учебно-методических комплексов по математике для общеобразовательной школы способствует повышению уровня математической подготовки учащихся, развитию их интереса к предмету, что в целом способствует совершенствованию процесса обучения математике.
Для изучения современного состояния практики осуществления преемственности в обучении математике между начальным и основным средним уровнями образования было проведено анкетирование учителей, работающих в пятых классах школ города Астаны. В анкетировании приняли участие 24 (100%) учителя математики школ №15, №51, №64. Среди них 8% (2) учителей математики со стажем работы в школе до 5 лет, 21% (5) учителей со стажем работы в школе от 5 до 10 лет, 46% (11) - от 10 до 20 лет и свыше 20 лет - 25% (6) учителей математиков (рис. 23).
Приведем итоги анкетирования, проведенного среди учителей математики, работающих в 5 классах. На вопрос анкеты: «Какие проблемы возникают в начале учебного года у учащихся при обучении математике в 5 классе?» было выявлены следующие основные недостатки: - в математической подготовке учащихся начальных классов школы. Все учителя отмечают плохое знание детьми таблиц умножения и 50% учителей математиков - несформированность у пятиклассников навыков устного счёта. - Указание учителей математиков в соответствии со стажем их работы на несформированность навыков устного счёта как проблему, возникающую в начале учебного года при обучении учащихся математике в 5 классе даны на рисунке 24. - у 38% из числа опрошенных учителей математиков возникают проблемы в обучении решению текстовых задач.
Указание учителей математиков в соответствии со стажем их работы на несформированность умений решения текстовых задач как проблему, возникающую в начале учебного года при обучении учащихся математике в 5 классе изображены на рисунке 25. - в организации процесса обучения математике. Так, почти половина (46%) из числа опрошенных учителей математиков отметили, что у детей не сформированы навыки самостоятельной работы, пятая часть (21%) - что учащиеся всё время ждут помощи.
В зависимости от стажа работы учителя, указанная проблема отмечена учителями в соотношении, изображённом соответственно на рисунках 26 и 27. - четвёртая часть (25%. Из них по указанному выше стажу соответственно: 0%; 0%; 33%; 67%) учителей математиков указали на неорганизованность учащихся; - третья часть (33%. Из них по указанному выше стажу соответственно: 0%; 13%; 50%; 37%) - что нет скорости выполнения заданий; - в контрольно-оценочной деятельности учителей начальных классов школы, которые привели к тому, что дети учатся ради оценок (это отметили более половины (54%) из числа опрошенных учителей математики), при получении низких оценок дети плачут (отметили 33% учителей пятых классов).
В зависимости от стажа работы учителя, указанная проблема отмечена учителями в соотношении, изображённом соответственно на рисунках 28 и 29. - большинство опрошенных учителей математиков (75%) указали на важность развития математической речи учащихся.
В зависимости от стажа работы учителя, ответы на этот вопрос отмечены учителями в соотношении, изображённом на рисунке 30. Развитие математической речи До 5 л ет 5-Юлет 11-20 лет Ют20лет - 17% учителей математики, отвечая на этот вопрос анкеты, указали на необходимость знания математики учителем начальных классов.
В зависимости от стажа работы учителя, ответы на этот вопрос отмечены учителями в соотношении, изображённом на рис. 31. Анализируя ответы учителей математиков на второй вопрос анкеты: «В Вашей практике обучения пятиклассников, какие темы по математике вызывали особые затруднения у учащихся?» оказалось, что особые затруднения у учащихся вызывает: - выполнение деления (отметили все опрошенные 24 учителя, т.е. 100%); - решение уравнений (отметили 88% учителей математиков: по указанному выше стажу соответственно: 14%; 18%; 41%; 27%); - решение текстовых задач (отметили 83% учителей математиков: по указанному выше стажу соответственно: 5%; 20%; 45%; 30%); - нахождение значений выражений, в которых несколько арифметических действий (отметили 67% учителей математиков: по указанному выше стажу соответственно: 8%; 6%; 44%; 38%); - выполнение умножения (отметили 50% учителей математиков: по указанному выше стажу соответственно: 8%; 17%; 33%; 42%); - решение логических заданий (отметили 33% учителей математиков: по указанному выше стажу соответственно: 0%; 12%; 38%; 50%).
С учетом выявленных критериев был осуществлён отбор и разработка упражнений для углубленного изучения математики, алгебры, алгебры и начал анализа учащимися, выбравшими одно из направлений: естественно-математическое или общественно-гуманитарное.
Нами предложены пути использования учеб но-мето дичее ко го комплекса по математике при обучении учащихся и даны рекомендации применения определенного пути для развития умения работы с учебной литературой. При этом использование учителем учебников и учебно-методического комплекса по математике помогло повысить качество знаний учащихся, их интерес к математике. Результаты проведенного эксперимента подтвердили выдвинутую гипотезу исследования.