Содержание к диссертации
Введение
ГЛАВА 1. Обзор методов измерении быстро меняющихся процессов 24
1.1. Применение динамических моделей 24
1.2. Динамические модели как инструмент описания хаотических процессов 29
1.2.1. Примеры хаотических процессов и систем 30
1.2.1.1. Детерминированный хаос 30
1.2.1.2. Диссипативные системы 32
1.2.2. Динамические модели 35
1.2.2.1. Описание динамических моделей 35
1.2.2.2. Виды динамических моделей 35
1.3. Квазистационарные динамические модели использующие авторегрессию с внешними входами 37
1.3.1. Линейные модели (ARX, ARMAX) 39
1.3.2. Нелинейные модели (NARX, NARMAX) 41
1.4. Выводы 46
ГЛАВА 2. Описание результатов измерении нестационарных температур с помощью алгоритмов построения нелинейных моделей 47
2.1. Представление методов измерения нестационарных температур 48
2.2. Фильтр Кал мана как метод коррекции динамических погрешностей при измерении нестационарных температур 52
2.3. Понятие динамических погрешностей 55
2.4. Выводы 57
ГЛАВА 3. Применение метода narmax для описания измерений нестационарных температур 58
3.1. Алгоритмы построения нелинейных динамических моделей
3.1.1 OLS алгоритм 58
3.1.2 FROLS алгоритм 62
3.2. Принцип действия метода NARMAX для построения нелинейных динамических моделей
З. З. М етодика исследования 6 7
3.4. Применение метода NARMAX для коррекции динамических погрешностей при измерении нестационарных температур 69
3.5. Результаты построения нелинейных динамических моделей и их исследование 78
3.5.1. Построение модели экспериментально зарегистрированных колебаний зданий (SISO случай) 78
3.5.2. Обработка синхронно зарегистрированных рядов наблюдений температурных колебаний при дыхании и сердцебиения (кардиопотенциала) (MISO - случай) 84
3.5.3. Построение модели концентрации углекислого газа при дыхании человека совместно с давлением воздуха при вдохе и выдохе человека (МІМО - случай) 90
3.6. Выводы 95
ГЛАВА 4. Результаты описания экспериментов с помощью динамических моделей 96
Выводы 116
Заключение 117
Литература
- Примеры хаотических процессов и систем
- Фильтр Кал мана как метод коррекции динамических погрешностей при измерении нестационарных температур
- Применение метода NARMAX для коррекции динамических погрешностей при измерении нестационарных температур
- Построение модели концентрации углекислого газа при дыхании человека совместно с давлением воздуха при вдохе и выдохе человека (МІМО - случай)
Введение к работе
Актуальность работы
и в
Нерегулярные хаотические процессы широко распространены в природе технике. К ним следует отнести турбулентное движение жидкостей и газов, связанное с процессами дыхания живых организмов, кипение жидкостей, а также колебания зданий и т.п., поэтому поведение температуры при её измерениях в турбулентных течениях жидкостей или газов имеет аналогичную структуру, то есть нерегулярную и хаотическую.
Для измерения температуры в указанных процессах часто приходится применять датчики, обладающие значительной инерционностью, которые могут не успевать реагировать на резкие скачки температуры в ходе измерений.
То же можно сказать и об измерениях других, быстроменяющихся физических величин как, например, изменение давления, концентрации газа, механические и акустические колебания.
Массивы информации, образующиеся при измерениях
быстроменяющихся процессов, занимают значительные объёмы. Их компактное, сжатое описание могло бы существенно сократить требуемые для хранения объёмы памяти. Такое аналитическое описание помогло бы решить и задачу коррекции динамических характеристик датчиков. Исходя из сказанного, можно выделить следующие задачи обработки экспериментальных данных:
-
Создание динамических моделей быстроменяющихся, в том числе, хаотических процессов;
-
Применение этих моделей для хранения информации об указанных процессах в сжатой форме; для динамической фильтрации, осуществляемой в процессе измерения; для динамической коррекции сигнала с выхода инерционного датчика.
Такие вопросы как хранение данных в сжатой форме, прогнозирование в процессе мониторинга, фильтрация временных рядов наблюдений, например, температурных измерений, требуют решения с помощью построения моделей процессов. Существуют также задачи, требующие описания хаотических нестационарных процессов при помощи методов динамического моделирования.
Динамическое моделирование подразумевает представление
наблюдаемого процесса в виде так называемого «серого ящика», внутренняя структура которого отражает особенности исследуемого процесса. Динамическая модель должна подстраиваться под исследуемый процесс так, чтобы не потерять его характерные особенности. Динамические методы применяются для теоретического описания и анализа систем и процессов, а также практического создания их моделей - как линейных, так и нелинейных.
Актуальность работы обусловлена рядом преимуществ применений нелинейных динамических моделей:
- возможность описания обширной области нелинейных динамических
процессов, таких, например, как процессы дыхания и сердцебиения у человека,
а также колебания зданий и сооружений т.п.;
— возможность выполняв фильтрацию потока данных - результатов
измерений в темпе измерения с одновременным построением модели.
Например, в работах [1-7] был проведен анализ колебаний воздуха в носовых ходах человека. Выявлено, что они носят нелинейный характер и являются хаотическими. В этих работах были исследованы такие характеристики этих процессов, как спектральная плотность мощности (СИМ) и хаотические инварианты: корреляционная размерность и корреляционная энтропия. Отсутствие аналитического описания для таких процессов приводит к необходимости хранить значительные массивы информации. Наличие такого, сжатого, описания с применением нелинейных динамических моделей, позволило бы существенно упростить их анализ.
Для описания процессов колебания температуры в различных средах, давления воздуха и концентрации СО2, автором была разработана и применена компактная компьютерная модель, которая существенно уменьшила затраты вычислительных ресурсов для хранения и анализа результатов этих измерений.
Особенностью этой модели является то, что она, несмотря на свою компактность, сохраняет все характеристики исходных процессов. Для этого автор разработал и применил компьютерную программу на основе алгоритмов реализующих нелинейное динамическое моделирование.
Динамические погрешности измерений хаотических, быстроменяющихся процессов, могут внести существенный вклад в общую погрешность измерения. Особенно это актуально для температурных измерений, когда по ряду причин датчик имеет значительные размеры и неспособен реагировать на быстрые изменения температуры. Расширение возможностей существующих методов и средств измерений температуры с помощью динамических моделей позволит снизить динамическую погрешность измерения.
Цель работы состоит в расширении возможностей существующих методов и средств измерений температуры на основе применении метода нелинейного динамического моделирования, а также для сжатого описания нерегулярных хаотических процессов и применения этого описания для решения следующих задач:
Экспериментального исследования живых систем, на основе измерений температуры, давления и концентрации углекислого газа;
Динамической коррекции показаний инерционных датчиков температуры;
Нелинейной фильтрации экспериментальных данных;
Анализа результатов колебаний зданий. Задачи:
Выбор метода для создания динамических моделей быстроменяющихся, в том числе, хаотических процессов;
Применение этого метода для построения моделей, способных хранить информацию об указанных процессах в сжатой форме;
Применение этого метода для динамической фильтрации и динамической
коррекции экспериментальных данных указанных хаотических процессов.
Объемами исследований являются процессы, протекающие в живых и технических системах, к которым относятся процессы дыхания и сердцебиения у человека, а также колебания зданий и сооружений и т.п.
Предметом исследования являются результаты измерений температуры, давления концентрации газов и вибраций, протекающих в нестационарном, хаотическом режиме, и применение для их анализа и их описания нелинейных динамических моделей.
Методы исследований основаны на применении динамических моделей для решения указанных задач.
Научная новизна диссертационной работы:
Впервые было выполнено нелинейное динамическое моделирование для сжатого описания процессов с проверкой адекватности описания на основе сравнения корреляционной размерности и энтропии для исходного процесса и его нелинейной динамической модели;
Метод впервые был применен для динамической коррекции реакции датчиков температуры на изменение температуры;
Метод нелинейного динамического моделирования был применен для нелинейной фильтрации экспериментальных данных.
Корректность моделей и полученных с их помощью результатов была подтверждена путем вычисления и сравнения между собой СПМ, корреляционной размерности и корреляционной энтропии параллельно для исходных данных и для полученных для них нелинейных моделей.
Теоретическая ценность полученных результатов состоит в новом подходе к описанию нелинейных динамических процессов как новой измерительной технологии, протекающих в живых и технических системах.
Практическая ценность полученных результатов состоит в разработке нелинейных динамических моделей температурных измерений процессов, протекающих в живых и технических системах, являющихся продуктом функционирования детерминированных систем.
В ходе выполнения работы на основе модельного сжатого описания были решены следующие проблемы, которые были вынесены на защиту.
Положения, выносимые на защиту:
-
Построена компактная нелинейная динамическая модель для описания процесса дыхания, состоящая из 3-7 коэффициентов и сохраняющая все характеристики исходного процесса [8-Ю].
-
Получена экспериментальная нелинейная динамическая модель, корректирующая показания инерционного термоприёмника. Проведена экспериментальная проверка этой модели сравнением с показаниями малоинерционного приемника.
-
Алгоритм модификации a-матрицы нелинейной динамической модели, на основе которого получен и опробован алгоритм динамической фильтрации экспериментальных данных. Адекватность и правильность
фильтрации подтверждена сравнением значений хаотических инвариант фильтруемых и отфильтрованных сигналов, а именно, корреляционной размерностью и энтропией.
Апробация результатов исследования:
Основное содержание работы докладывалось на следующих научных конференциях:
VIII Всероссийская межвузовская конференция молодых ученых (Санкт-Петербург, Россия, 2011 г.);
I Всероссийский конгресс молодых ученых (Санкт-Петербург, Россия,
2012 г.);
XLII научная и учебно-методическая конференция НИУ ИТМО (Санкт-Петербург, Россия, 2013 г.)
II Всероссийский конгресс молодых ученых (Санкт-Петербург, Россия,
2013 г.).
I международная конференция «Сенсорика» (Санкт-Петербург, Россия,
2013 г.).
XLIII научная и учебно-методическая конференция НИУ ИТМО (Санкт-Петербург, Россия, 2014 г.)
III Всероссийский конгресс молодых ученых (Санкт-Петербург, Россия,
2014 г.).
II международная конференция «Сенсорика» (Санкт-Петербург, Россия,
2014 г.).
XLIV научная и учебно-методическая конференция НИУ ИТМО (Санкт-Петербург, Россия, 2015 г.)
IV Всероссийский конгресс молодых ученых (Санкт-Петербург, Россия,
2015 г.).
Результаты диссертации опубликованы в 4 научных публикациях, в т.ч. 3 - в изданиях, рекомендованных ВАК РФ.
Личный вклад автора
Диссертация написана лично автором под руководством его научного руководителя. Все результаты, полученные в ходе исследования и отраженные в настоящей диссертации, получены автором лично или при его непосредственном участии.
Структура и объем работы:
Диссертация состоит из введения, четырех глав, заключения, списка цитируемой литературы и 2 приложений.
Примеры хаотических процессов и систем
В настоящее время динамические модели получили широкое распространение в различных сферах человеческой деятельности. Сегодня они нашли применение от технических до гуманитарных наук, также от теоретического описания процессов протекающих в природе и в технике до фильтрации данных в режиме их непрерывного поступления [1,4,17].
Построение динамических моделей основано на сборе и обработке статистических данных описываемых реальных и искусственно созданных процессов и систем. При этом методика построения динамических моделей включает в себя как математическое моделирование, а именно, алгоритмы построения динамических моделей, так и компьютерное моделирование, то есть непосредственное создание компьютерной динамической модели на основе данных алгоритмов. Динамическое моделирование может быть использовано для обработки данных процессов, например, фильтрации экспериментальных данных, непосредственно измерительной установкой или прибором, содержащими в себе, например, бортовые системы фильтрации данных [15], построенные на основе динамического моделирования. Исходя из вышесказанного, динамическое моделирование использует один из основополагающих принципов построения математических моделей: «от данных до модели», где система, с которой идёт сбор информации в виде статистических данных, представляется в виде так называемого «серого ящика», внутренняя структура которого отражает особенности исследуемого процесса. При построении динамической модели такого процесса данные особенности оказывают влияние на параметры уже созданной модели процесса, изменяя которые можно экспериментальным путём исследовать системы и процессы. Соответственно, динамические модели применяются для теоретического анализа систем и процессов, практического создания моделей систем и процессов, а также для фильтрации экспериментальных данных.
Применение динамического моделирования для построения моделей реальных процессов и систем включает в себя решение обратной задачи математического моделирования, когда необходимо выбрать конкретную модель на основании дополнительных данных об исследуемом процессе или описываемой системе. Такими данными могут быть результаты специально планируемых в ходе решения задачи экспериментов.
В 1980-ые годы на основе алгоритма метода наименьших квадратов и авторегрессии скользящего среднего значения с внешними входами был разработан профессором Шеффилдского университета Стивом Биллингсом и его коллегами метод NARMAX (Nonlinear Auto Regressive Moving Average with eXogenous inputs), то есть метод нелинейного авторессионного скользящего среднего с внешними входами. Этот метод состоит в ряду с такими методами как ARX (Auto Regression with eXogenous inputs), ARMAX (Regressive Moving Average with eXogenous inputs) и NARX (Nonlinear Auto Regression with eXogenous inputs), рассмотрение которых будет продолжено далее. В данном исследовании в качестве одного из примеров применения динамического моделирования проиллюстрировано и проанализировано применение метода или модели NARMAX для создания динамических моделей и описания живых и технических систем.
Применение динамических моделей для анализа систем и процессов включает в себя анализ систем, оценку устойчивости и прогнозирование поведения процессов [1].
Согласно определению понятия анализа систем, при котором системный анализ определяется как научный метод познания, представляющий собой последовательность действий по установлению структурных связей между переменными или элементами исследуемой системы, динамические модели при анализе систем применяются в качестве инструмента оценки структурных связей между переменными или элементами исследуемой системы. [2,3]
Соответственно, применение динамических моделей при анализе систем в контексте оценки исследования компонентов описываемой системы необходимо для решения: во-первых, слабоструктурированных задач, связанных с исследованиями так называемых «серых ящиках», при которых в системах состав элементов и взаимосвязей установлен только частично; во-вторых, задач возникающих, как правило, в ситуациях, характеризуемых наличием фактора неопределенности, которые требуют оценки устойчивости поведения систем или процессов. [5]
Динамическое моделирование, применяющееся для оценки устойчивости поведения процессов, представляет собой аналитическую структуру, которая определяет устойчивость процесса при заданных значениях его параметров, в каких диапазонах можно изменять параметры процесса или системы, не нарушая свойства устойчивости, какой характер имеет свободное движение процесса. Для устойчивой системы необходимо, чтобы свободная составляющая процесса с течением времени стремилась к нулю. Если динамическое моделирование процесса даёт определённую оценку устойчивости поведения процессов или систем, то можно с большой долей вероятности прогнозировать поведение процессов или систем. [4] Прогнозирование поведения процессов при помощи динамического моделирования позволяет регулировать как общее состояние исследуемых систем, так и отдельных структурных компонентов систем. Регулирование осуществляется при помощи действия механизма обратной связи, который оказывает влияние уже не собственно на модель процесса, а на сам процесс. То есть, при помощи действия модели процесса можно спрогнозировать поведение процесса и оказать на него влияние таким образом, что с большой долей вероятности система останется максимально устойчивой. При этом при помощи прогнозирования поведения процессов осуществляется их управление. Управление поведением процессов необходимо для обеспечения жизнеспособности живых систем и стабильной работы технических систем. [15,16]
Динамическое моделирование в исследованиях живых систем является инструментом для изучения, в частности, физиологических процессов, которыми в данном исследовании являются процессы дыхания и сердцебиения. Применение динамического моделирования в данном случае представляет собой гибкий подход к анализу закономерностей естественных флуктуации состояния человеческого организма под воздействием эндо и экзогенных факторов. Динамическое моделирование включает создание специальной технологии, основанной на комплексе математических моделей, описывающих динамику интегральной деятельности целостного организма или функции его структурных единиц - органов, то есть исследования цикла дыхания и кардиоцикла, согласно экспериментальным исследованиям, проведённым в ходе работы над диссертацией. Динамическое моделирование создает предпосылки для имитационных исследований причинно-следственных отношений в организме виртуального или находящегося дистанционно пациента, а также исследования в организме пациента без его физического присутствия. Динамическое моделирование в исследованиях живых систем может стать дополнительным инструментарием в медицине при диагностике состояния и проверки эффективности лечения. [12,16,19] Динамическое моделирование в исследованиях технических систем в отличие от исследований живых систем необходимо не только для исследования собственно технической системы, но и для оценки соответствия технической системы заданным параметрам. Динамическое моделирование в исследованиях технических систем применяется для диагностики технического состояния основ конструкций и обеспечения стабильной работы технологических процессов и систем. При таком подходе в исследованиях невозможно обходиться без фильтрации экспериментальных данных средствами динамического моделирования. [11]
Применение динамического моделирования для фильтрации экспериментальных данных представляет собой механизм очистки таких данных от всевозможных шумов и нежелательных частот. Фильтрация экспериментальных данных необходима для получения более точного сигнала, который был получен на основе статистических данных.[15]
Фильтр Кал мана как метод коррекции динамических погрешностей при измерении нестационарных температур
Исходя из выше представленного, приведено описание математических моделей, как процесса теплопереноса, так и измерений в различных типах сенсоров нестационарного теплового потока; рассмотрены алгоритмы программ для решения прямых и обратных задач теплопроводности. Для получения оценок значений теплового потока разработаны программы двух модификаций фильтра Калмана, которые позволили оценить поток в реальном времени.
Приведены результаты математического моделирования по восстановлению теплового потока и уточнению теплопроводности материала, которые позволяют утверждать, что разработанные методики расчетов могут быть использованы в энергосберегающих технологиях, в частности, при определении тепловых потерь ограждающих конструкций зданий и сооружений в нестационарном режиме. [17,20]
Представленные результаты математического моделирования, использующие фильтр Калмана, сводятся к применению 3-сплайнов, не обладающих механизмом обратной связи, в отличие от метода NARMAX. При которой идёт выбор степени многочлена модели. Также в расширенной нелинейной версии фильтра Калмана имеется локальная линеаризация.
То есть, фильтр Калмана не может подстраиваться под реальные быстроизменяющиеся процессы и адекватно их описывать. Особенно, если необходимо построить нелинейные динамические модели процессов, которые имеются в природе и технике, так как реальные процессы в природе и технике являются нелинейными и динамическими в подавляющем большинстве случаев. Поэтому следует рассмотреть применение метода NARMAX для коррекции динамических погрешностей при измерении нестационарных температур.
Согласно определению, динамические погрешности - это погрешности, численное значения которых вычисляются как разности между погрешностями, возникающих при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени). В данном диссертационном исследовании измеряемой величиной является температура. Статическая погрешность измерений, в свою очередь - это погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.
Динамическая погрешность измерений - погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средства измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.
Так как изменение температуры со временем в основном имеет нестационарный характер, в частности в процессе кипячения воды, то для устранения динамических погрешностей температурных измерений может быть применено нелинейное динамическое моделирование.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины. [36]
Применение метода NARMAX для коррекции динамических погрешностей при измерении нестационарных температур
Представлены результаты экспериментально синхронно зарегистрированных рядов наблюдений, полученных на основе исследований, которые проводят Г.Н. Лукьянов совместно с И.С. Ковальским и А.Г. Малышевым Цель исследования: апробация построения нелинейных динамических MIMO (multi input multi output, то есть много входных и много выходных) моделей на примере модели NARMAX имеющей три входа и два выхода. Задача исследования построение модели NARMAX имеющей три входа и два выхода. Исходные данные: в этом исследовании исходными данными являются экспериментально зарегистрированные ряды наблюдений концентрации углекислого газа при дыхании человека (рис. 3.33.) совместно с синхронно зарегистрированными рядами наблюдений давления воздуха при вдохе и выдохе человека (рис. 3.34, 3.35.).
График зависимости давления воздуха в левой ноздре при дыхании человека от времени Методика исследования: экспериментально зарегистрированные ряды наблюдений концентрации углекислого газа подаются на первый вход MIMO NARMAX модели, синхронно зарегистрированные ряды наблюдений давления воздуха при вдохе и выдохе человека из каждой ноздри поданы на второй и третий вход в модель соответственно. На первый выход подана общая модель зависимости концентрации углекислого газа от давления воздуха в первой ноздре. На второй выход подана общая модель зависимости концентрации углекислого газа от давления воздуха во второй ноздре. Это показано на рисунке 3.36.
Проведено исследование возможностей применения метода NARMAX для построения моделей согласно указанной методике в нескольких вариантах: SISO, MISO и MIMO, то есть один вход в модель и один выход из модели, много входов в модель и один выход из модели, много входов в модель и много выходов из модели, соответственно. На основе метода NARMAX проведена динамическая коррекция показаний инерционного датчика температуры на основе термистора для его использования без термопары, также проведено исследование колебаний зданий, создана статистическая динамическая модель, описывающая как процессы дыхания и сердцебиения в отдельности, так и во взаимосвязи, проведено исследование концентрации углекислого газа совместно с давлением воздуха при дыхании человека. Метод NARMAX адекватно описывает исследуемые процессы и может быть применен для построения моделей разной природы.
В данной главе рассматриваются результаты описания экспериментов с помощью динамических моделей, а именно, при помощи метода или модели NARM АХ.
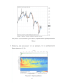
На рисунке 4.1. представлено измерение среднесуточной температуры воздуха в Санкт-Петербурге за несколько лет. Измерение среднесуточной температуры воздуха в Санкт-Петербурге выделено синим, модель процесса измерения среднесуточной температуры выделено красным.
Исходя из представленного на рисунке графика видно, что моделью NARMAX можно описывать процесс измерения среднесуточной температуры воздуха.
Для проверки правильности настройки алгоритма NARMAX была произведена серия экспериментов по обработки временных рядов кардиограммы и сигналов с помехами, то есть процесса измерения кардиопотенциала и фильтрации помех при работе с датчиком для измерения кардиопотенциала.
Результаты моделирования и фильтрации данных в этих экспериментах не были нормированы, так как задачи нормирования данных в этих экспериментах не было.
Моделируемый или фильтруемый сигнал выделен синим цветом, модель процесса или отфильтрованный сигнал выделен красным цветом. На оси абсцисс обозначен номер временного ряда, а на оси ординат - значение кардиопотенциала в миливольтах. На увеличенных фрагментах, выделенных тёмно-синим прямоугольником, представлены характерные особенности фильтруемых сигналов.
Построение модели концентрации углекислого газа при дыхании человека совместно с давлением воздуха при вдохе и выдохе человека (МІМО - случай)
Стационарные динамические модели - это модели, имеющие не изменяющиеся со временем свойства преобразования входных переменных, в противном случае такие динамические модели называются нестационарными. Также выделяют так называемые квазистацинарные модели, в которых параметры системы изменяются в зависимости от времени, то есть модели, одновременно обладающие свойствами как стационарных моделей, так и нестационарных. Для идентификации динамических моделей обыкновенно применяется классическая нормальная линейная модель наблюдений y{t) = Yii=ixi(X)@i + (O? t= 1, 2, ...,n, (1-0? в которой предполагается, что значения объясняющих переменных xtl, xt2,..., xtp, t = 1,2, ..., n, фиксированы, а случайные составляющие є 1, є 2, ..., є п("ошибки") являются независимыми случайными величинами, имеющими одинаковое нормальное распределение с нулевым математическим ожиданием и конечной дисперсией. При этом в данном случае работает основополагающий принцип построения математических моделей, в частности динамических, от данных до модели.
Согласно классической нормальной линейной модели наблюдений выделяются модели временных рядов, построенные на основе результатов измерений. К таким моделям временных рядов относят модели временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени. Эти модели, в свою очередь, условно разделены на три группы. [56] а) модели с распределённым лагом (лаг от англ. lag - задержка) - это модели временного ряда, в которых в уравнение регрессии включено как текущее значение независимой переменной, так и значения этой переменной в предыдущих периодах. б) модели авторегрессии скользящего среднего (англ. autoregressive moving-average model, ARM A) — одни из математических моделей, использующихся для анализа и прогнозирования стационарных временных рядов в статистике. Модель ARMA обобщает две более простые модели временных рядов — модель авторегрессии (AR) и модель скользящего среднего (МА); в) модели адаптивных ожиданий, учитывающие предполагаемое или желаемое значение независимой переменной, в которых ожидания постепенно корректируются в соответствии с фактическими значениями данной переменной.
Квазистационарные динамические модели следует рассмотреть более подробно из-за их специфических возможностей, а именно, описания квазистационарных процессов, в которых имеется структура, состоящая из жесткого каркаса в виде стационарных состояний процесса и хаотических флуктуации процесса, не искривляющих этот жесткий каркас. Среди квазистационарных динамических моделей важное место занимают модели, использующие авторегрессию с внешними входами. Это связано с тем, что авторегрессия с внешними входами позволяет адаптивно подстроить получаемую динамическую модель под исследуемый процесс. [56]
Как было отмечено ранее, что квазистационарные динамические модели обладают характеристиками, как стационарных динамических моделей, так и нестационарных. Использование квазистационарных динамических моделей необходимо для описания квазистационарных состояний процессов и систем.
Квазистационарные процессы - это процессы, протекающие и распространяющиеся в ограниченных системах так быстро, что за время распространения этих процессов в пределах таких систем, их состояния не успевают измениться. Время в данном случае понятие условное, так как процессы рассматриваются относительно временной шкалы как на микроуровне, так и на макроуровне. Согласно теореме Котельникова (в англоязычной литературе теореме Найквиста-Шеннона), которая связывает аналоговые и дискретные сигналы и гласит, что если аналоговый сигнал x(t) имеет ограниченный по ширине спектр, то он может быть восстановлен однозначно и без потерь по своим отсчётам, взятым с частотой, большей или равной удвоенной верхней частоте fc так, что / 2fc, динамическое моделирование использует дискретный сигнал, то есть цифровой сигнал.
Цифровой сигнал — сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений. Поэтому под временем в динамическом моделировании понимается дискретное время. Оно, в свою очередь связано с понятием временного ряда.
Временной ряд (или ряд динамики) — собранный в разные моменты времени статистический материал о значении каких-либо параметров (в простейшем случае одного) исследуемого процесса. Каждая единица статистического материала называется измерением или отсчётом, также допустимо называть его уровнем на указанный с ним момент времени (дискретного времени). Во временном ряде для каждого отсчёта должно быть указано время измерения или номер измерения по порядку. Временной ряд существенно отличается от простой выборки данных, так как при анализе учитывается взаимосвязь измерений со временем, а не только статистическое разнообразие и статистические характеристики выборки. [34]