Содержание к диссертации
Введение
Глава 1. Модели динамики и методы дистанционного зондирования наземных экосистем 14
1.1 Научные и прикладные задачи изучения динамики наземных экосистем на основе моделирования и методов дистанционного зондирования 14
1.2 Физические основы и методы мониторинга наземных экосистем на основе данных дистанционного зондирования в оптическом диапазоне
1.2.1 Спутниковое картографирование растительного покрова 20
1.2.2 Спутниковый мониторинг природных пожаров 29
1.3 Моделирование динамики наземных экосистем 34
1.3.1 Глобальные модели динамики растительного покрова 34
1.3.2 Модели распространения природных пожаров 42
1.4 Численные методы интеграции данных дистанционного зондирования в модели динамики наземных экосистем 47
Выводы к первой главе 55
Глава 2. Моделирование динамики растительного покрова на основе интеграции результатов спутникового картографирования 56
2.1 Глобальная модель динамики растительного покрова SEVER 56
2.2 Модификация модели динамики растительного покрова SEVER 61
2.3 Региональная параметризация модели динамики растительного покрова на основе интеграции результатов спутникового картографирования 68
Выводы ко второй главе 75
Глава 3. Моделирование развития природных пожаров на основе интеграции в модель их динамики данных дистанционного зондирования 76
3.1 Модель распространения природного пожара 76
3.2 Региональная параметризация модели распространения природных пожаров с использованием результатов спутникового детектирования очагов горения 83
3.3 Детерминированная и стохастическая модель прогнозирования динамики природных пожаров 87
3.4 Алгоритм оперативной оценки развития природных пожаров 92
3.5 Система оперативного прогнозирования развития природных пожаров на основе интеграции данных дистанционного зондирования 107
Выводы к третьей главе 112
Глава 4. STRONG Программный комплекс lagma-plus локально адаптивной классификации и оценивания характеристик наземных экосистем на основе данных дистанционного зондирования 113
4.1 Концепция метода LAGMA STRONG 113
4.2 Программная реализация метода LAGMA 121
4.3 Примеры практической апробации LAGMA-PLUS в технологиях оценки наземных экосистем 125
Выводы к четвертой главе 128
Заключение 129
Список литературы 131
- Спутниковый мониторинг природных пожаров
- Региональная параметризация модели динамики растительного покрова на основе интеграции результатов спутникового картографирования
- Детерминированная и стохастическая модель прогнозирования динамики природных пожаров
- Примеры практической апробации LAGMA-PLUS в технологиях оценки наземных экосистем
Введение к работе
Актуальность диссертационной работы
Наземные экосистемы являются важнейшей составляющей биосферы Земли и играют ключевую роль в фундаментальных процессах обмена веществом и энергией на планете. Растительный покров, как неотъемлемая компонента различных типов наземных экосистем планеты, покрывает около 80% земной поверхности и содержит почти 99% наземной биомассы. Растительность играет важную роль в глобальном цикле углерода, усваивая его из атмосферы в процессе фотосинтеза и выделяя в атмосферу в процессе дыхания и в почву в результате отмирания тканей.
В последние столетия деятельность человека значительно усилила свое влияние на наземные экосистемы. Массовые вырубки лесов и сельскохозяйственное использование земель приводят к трансформации наземных экосистем. К числу антропогенных последствий ряд ученых относит и увеличение содержания углерода в атмосфере, что предположительно играет значительную роль в наблюдаемых климатических изменениях. Состояние и ареал распространения растительного покрова Земли не остается неизменным в условиях меняющегося климата планеты. При этом наземные, и, в особенности, лесные, экосистемы являются одним из основных потребителей атмосферного углерода и потенциально способны скомпенсировать его антропогенные выбросы. Роль динамики растительного покрова в глобальных климатических и биосферных процессах приводит к необходимости мониторинга и прогноза его состояния.
Математическое моделирование является мощным инструментом изучения динамики наземных экосистем. Существует большое количество моделей динамики растительности, имеющих разную область применения и степень детальности, а также предназначенных для применения в различных условиях, как для оценки состояния наземных экосистем, так и для прогноза их динамики. Используемые на практике модели обычно основаны на упрощенных, описываемых эмпирическими уравнениями, представлениях о процессах, происходящих в наземных экосистемах. Поэтому для построения, настройки и верификации таких моделей важно наличие данных о процессах в наземных экосистемах.
До относительно недавнего времени практически единственным источником данных
о состоянии наземных экосистем и процессах в них являлись полевые обследования. Такой
подход не позволяет на практике обеспечить регулярность сбора данных на больших
территориях глобального или континентального уровней. Появление методов
дистанционного зондирования Земли (ДЗЗ) из космоса открыло принципиально новую возможность получения актуальной и регулярно обновляемой информацию о состоянии наземных экосистем на различных уровнях территориального охвата. Современные системы ДЗЗ позволяют получать информацию о характеристиках отраженного и собственного излучения земного покрова в различных диапазонах длин волн. К настоящему времени разработано большое количество методов получения информации о растительном покрове по данным измерений его спектрально-отражательных характеристик.
Спутниковые данные предоставляют принципиально новую возможность регулярного получения актуальной информации о состоянии наземных экосистем на больших
территориях. Это, в свою очередь, оказало значительное стимулирующее влияние на развитие подходов по интеграции результатов дистанционных измерений характеристик наземных экосистем в модели их динамики. Данные спутникового мониторинга могут интегрироваться в качестве входной информации в модели, применяться для их параметризации или коррекции модельных оценок результатами измерений (ассимиляция данных).
В диссертационной работе разработаны и апробированы численные методы и программные комплексы оценки состояния наземных экосистем на основе интеграции данных спутникового мониторинга в описывающие их динамику модели. Рассмотрены две модели наземных экосистем контрастно различных уровней:
глобальная модель динамики растительного покрова, воспроизводящая изменение пространственного распределения основных его типов на основе описания ключевых процессов роста растений с учетом влияния различных факторов, включая природные пожары;
локальная эмпирическая модель распространения природного пожара на основе данных о метеорологических условиях, типах и состоянии горючих материалов, рельефе местности.
Получение данных о состоянии наземных экосистем, необходимых для настройки, верификации и использования моделей, потребовало создания нового программного комплекса локально-адаптивного глобального картографирования. Данный программный комплекс позволил решить проблему автоматизации картографирования и оценивания многолетней динамики земного покрова на больших территориях, и, таким образом, обеспечил регулярное поступление актуальных данных для моделирования наземных экосистем.
Регионально адаптированные к условиям России модели наземных экосистем позволяют проводить оценку их состояния и динамики с использованием ограниченного набора данных, оперативно доступных для всей территории страны. Важность решения задач мониторинга наземных экосистем и практической сложности его проведения другими методами служит обоснованием актуальности диссертационной работы.
Современное состояние исследований в данной области. Вопросам моделирования динамики наземных экосистем и возмущающих воздействий в них (пожаров), в том числе и с использованием спутниковых данных, посвятили свои труды многие отечественные и зарубежные ученые: СВ. Веневский, А.М. Гришин, Г.А. Доррер, А.С. Комаров, Н.М. Чебакова, СИ. Чумаченко, F.A. Albini, М.А. Finney, P. Сох, W. Cramer, J. Mandel, 1С. Prentice, M. Rochoux, R.C Rothermel, S. Sitch, K. Thonicke. Но существующие модели наземных экосистем обычно проверяются на ограниченном количестве примеров или не адаптированы для использования на территории России, что затрудняет их применение для оценки и прогнозирования динамики наземных экосистем в масштабах страны.
Цель и задачи исследований. Целью проведенных исследований являлась разработка численных методов, имитационных моделей и комплексов программ для исследования и прогнозирования динамики наземных экосистем на основе интеграции данных спутникового мониторинга, которые позволят повысить эффективность решения
задач управления природными ресурсами и охраны окружающей среды. Достижение вышеуказанной цели диссертационной работы потребовало решения следующих задач исследований и разработок:
анализ математических моделей динамики растительного покрова, обеспечивающих потенциальную возможность мониторинга и прогноза состояния наземных экосистем путем ассимиляции спутниковых данных ДЗЗ;
анализ возможностей использования спутниковых данных ДЗЗ для картографирования и мониторинга растительного покрова;
разработка многопоточного программного комплекса LAGMA-PLUS (Locally Adaptive Global Mapping Algorithm PLUS) для решения задач глобального спутникового картографирования и оценивания характеристик наземных экосистем на основе спутниковых данных ДЗЗ;
региональная адаптация моделей динамики растительного покрова на основе интеграции данных спутникового мониторинга, обеспечившая качественное повышение достоверности результатов моделирования на территории России;
региональная параметризация имитационной модели распространения пожара на основе данных спутникового мониторинга динамики очагов горения;
разработка алгоритма вероятностного прогнозирования развития природных пожаров на основе метода Монте-Карло с ассимиляцией данных спутникового мониторинга в модель распространения кромки горения;
разработка алгоритма оперативного уточнения положения фронта пожара на основе ассимиляции данных спутникового мониторинга в имитационную модель динамики распространения огня;
программная реализация системы оперативной оценки и прогнозирования динамики лесных пожаров на основе регионально параметризованной математической модели их развития и результатов спутникового детектирования очагов горения.
Методы исследований. В работе использованы численные методы, методы математического моделирования, методы дистанционного зондирования Земли, методы статистического анализа, методы классификации изображений, методы оптимизации и прикладного программирования.
Научная новизна работы
-
Впервые на основе данных спутникового картографирования растительного покрова проведена региональная параметризация глобальной модели его динамики, позволившая существенно повысить достоверность результатов моделирования на территории России;
-
Разработана модификация глобальной модели динамики растительности, позволяющая учитывать процессы конкуренции за свет между растениями, влияние климатических факторов на формирование тундры, существенно повысившая достоверность результатов моделирования;
-
Разработана регионально адаптированная и параметризованная на основе данных спутникового мониторинга модель динамики природного пожара, обеспечивающая
возможность оперативного моделирования распространения огня на всей территории России с использованием информации спутниковых и метеорологических наблюдений;
4 Предложен новый алгоритм оперативного уточнения положения фронта пожара на
основе ассимиляции данных спутникового мониторинга в имитационную модель динамики распространения огня.
Основные защищаемые результаты.
-
Регионально адаптированная на основе результатов спутникового картографирования и модифицированная (учет конкуренции за свет между деревьями и климатических факторов формирования тундры) глобальная модель динамики растительности, обеспечивающая повышение качества результатов моделирования;
-
Регионально адаптированная модель динамики природного пожара и комплекс программ, обеспечивающие возможность оперативного детерминистического и стохастического (методом Монте-Карло) прогнозирования распространения огня на территории России по данным спутниковых и метеорологических наблюдений;
-
Алгоритм оперативного уточнения оценки положения фронта пожара на основе ассимиляции результатов дистанционного детектирования очагов горения в модель динамики распространения огня;
-
Программный комплекс локально-адаптивной классификации и оценивания характеристик земного покрова на основе автоматизированной многопоточной обработки данных дистанционного зондирования, обеспечивающий возможность регулярного спутникового картографирования наземных экосистем на больших территориях.
Практическая значимость. Система оперативного прогнозирования развития очагов горения широко используется в составе Информационной системы дистанционного мониторинга лесных пожаров Федерального агентства лесного хозяйства Российской Федерации (ИСДМ-Рослесхоз).
Программное обеспечение LAGMA-PLUS нашло активное применение в решении задач спутникового картографирования наземных экосистем России, в том числе при создании многолетних рядов карт типов растительного покрова, карт используемых сельскохозяйственных земель, видового состава лесов и запасов стволовой древесины в лесах.
Параметризованная модель динамики растительного покрова позволяет осуществлять прогнозирование состояния наземных экосистем России с учетом различных сценариев климатических изменений.
Соответствие паспорту специальности. Содержание работы соответствует п. 4 «Реализация эффективных численных методов и алгоритмов в виде комплексов проблемно-ориентированных программ для проведения вычислительного эксперимента», п. 5 «Комплексные исследования научных и технических проблем с применением современной технологии математического моделирования и вычислительного эксперимента», п. 7 «Разработка новых математических методов и алгоритмов интерпретации натурного эксперимента на основе его математической модели» и п. 8 «Разработка систем компьютерного и имитационного моделирования»
Апробация работы. По результатам данной работы было сделано 14 докладов на российских и международных конференциях в Москве, Санкт-Петербурге и Томске. Автор трижды (2011, 2012 и 2014 годы) становился призером конкурса Всероссийской конференции «Современные проблемы дистанционного зондирования Земли из космоса» за лучший доклад молодого ученого.
Личный вклад. Автор лично разработал программное обеспечение модели распространения природных пожаров и метода ассимиляции в нее данных спутникового мониторинга, а также осуществил региональную адаптацию моделей динамики наземных экосистем. Автор лично выполнил работы по развитию алгоритма LAGMA и разработке программного комплекса LAGMA-PLUS для многопоточной обработки данных дистанционного зондирования с целью локально-адаптивной классификации и оценивания характеристик земного покрова.
Публикации. По результатам исследований и разработок опубликовано более 20 печатных работ, в том числе 7 научных статей в журналах из списка, рекомендованного ВАК РФ.
Структура и объем диссертации. Диссертация состоит из введения, четырех глав, заключения, библиографического списка, включающего 153 наименования, и приложений. Объем диссертации составляет 151 страницу машинописного текста, 22 рисунка и 7 таблиц.
Спутниковый мониторинг природных пожаров
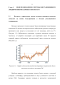
Природные пожары являются причиной эмиссии около 2 GtC ежегодно [35]. Стоит отметить, что появление новой растительности на лесных гарях с течением времени компенсирует эмиссию углерода в атмосферу от пожаров. При неизменном распределении и количестве природных пожаров баланс углерода в растительности также преимущественно остается неизменным. Но изменение климата приводит к увеличению продолжительности пожарного сезона и, предположительно, к увеличению числа пожаров и их суммарной площади (особенно в бореальных регионах), что может сказаться и на углеродном цикле [34]. Увеличение количества и интенсивности пожаров может также повысить наносимый ими вред здоровью и жизни людей, объектам экономики и хозяйственной деятельности.
Происходящие изменения в климате планеты и зависимость людей от растительного покрова Земли обуславливает необходимость осуществления его мониторинга. В конце прошлого столетия для мониторинга динамики растительного покрова начали достаточно широко применяться методы дистанционного зондирования Земли из космоса и математические модели.
Возможность использования данных дистанционного зондирования для мониторинга растительности стала рассматриваться вскоре после появления первых спутниковых аппаратов. Например, в США этот вопрос начал широко обсуждаться в середине-конце 60-х годов. Именно в это время были разработаны планы первого спутника для наблюдения за земным покровом, выработаны и апробированы (преимущественно по данным аэрофотосъемки) технологии и методы применения данных ДЗЗ для мониторинга растительности. Наблюдение за состоянием растительности для решения задач в сферах сельского хозяйства, лесоводства и географии считалось одним из приоритетных направлений в развитии методов ДЗЗ [36]. В дальнейшем успешное применение первого аппарата серии Landsat (Earth Resources Technological Satellite - ERTS-1) продемонстрировало возможности мультиспектрального дистанционного зондирования и способствовало развитию этого направления [37].
В ранний период использования ДЗЗ для мониторинга растительности используемые данные были ограничены эпизодически доступными изображениями, а их анализ проводился преимущественно методами визуального дешифрирования. Автоматические алгоритмы и методы обработки ДЗЗ в то время использовались преимущественно скорее для демонстрации их потенциала, чем для решения реальных задач. С конца 90-х годов, по мере увеличения объема доступных спутниковых данных и изменения политики доступа к ним, ситуация начала меняться. Начиная с этого периода, появилась возможность осуществления регулярного мониторинга растительности на обширных территориях и решения задач континентального и глобального картографирования [38].
На данный момент на орбите Земли находится свыше 80 спутниковых аппаратов, способных осуществлять мониторинг растительного покрова на глобальном уровне [39]. В задачах мониторинга наземных экосистем наиболее широко используются данные спектрорадиометров, к числу которых относятся системы MODIS (Moderate-Resolution Imaging Spectroradiometer), Landsat, NPP-VIRS (Suomi National Polar-orbiting Partnership Visible Infrared Imaging Radiometer Suite) и ряд других. Получаемые указанными системами ДЗЗ данные позволили сформировать глобальные архивы многолетних измерений спектрально-отражательных характеристик земной поверхности. В последние годы можно отметить появление все большого количества гиперспектрометров (Hyperion, гиперспектральная аппаратура (ГСА) на Ресурс-П), радаров (Radarsat, TerraSAR), и других аппаратов, которые можно использовать для мониторинга растительности. Также можно отметить появление все большего числа аппаратов ДЗЗ (WorldView, GlobEye, Ресурс-П), осуществляющих съемку с детальным пространственным разрешением (размер пикселя изображения - от десятков сантиметров до единиц метров), хотя их применение пока еще часто ограничено малой областью захвата и высокой стоимостью данных.
Одно из основных преимуществ методов ДЗЗ перед другими источниками данных о наземных экосистемах состоит в возможности оперативного и регулярного получения актуальной информации о состоянии растительного покрова обширных территорий при достаточно малых затратах.
Региональная параметризация модели динамики растительного покрова на основе интеграции результатов спутникового картографирования
Модельный прогноз динамики наземных экосистем может быть точен только при использовании точных входных данных о состоянии окружающей среды (метеорология, почва и др.). Погрешности во входных данных моделей могут сильно влиять на качество прогнозов. Эта проблема особенно остро стоит при моделировании больших территорий, требующем значительного объема данных. Данные дистанционного зондирования дают возможность регулярно получать актуальную информацию о состоянии растительности, а интеграция этих данных в модели может значительно повысить качество моделирования.
Существует большое количество работ, посвященных совместному использованию данных ДЗЗ и моделей динамики растительности. Самый простой подход интеграции данных ДЗЗ в модели - это их применение в качестве входных данных. Например, модели могут использовать карты земного покрова [22] и карты с.х. полей [21], [24], полученные по данным ДЗЗ.
Также данные спутникового мониторинга могут быть использованы в качестве замены для некоторых параметров моделей наземных экосистем. При использовании такого подхода предполагается, что ошибка в оценке параметра по спутниковым данным достаточно мала. Такой подход, например, используется в работе [118], в которой была создана простая модель развития сельскохозяйственных посевов, индекс LAI в которой определялся по данным спутникового прибора AVHRR. Эта модель была успешно применена для прогнозирования урожайности риса и пшеницы в Пакистане.
Погрешности в оценке характеристик наземных экосистем по спутниковым данным могут помешать их прямому использованию в моделях. В таких случаях может быть использован подход, основанный на ассимиляции данных в модель. Этот подход основан на предположении наличия погрешностей в данных и модели, и предполагает итеративную коррекцию параметров модели по мере поступления новых данных. Задача ассимиляции данных часто решается с помощью фильтра Калмана и его вариаций. Пример использования такого подхода к ассимиляции данных можно найти в работе [24], где в модель роста сельскохозяйственных посевов ассимилировались спутниковые данные о LAI и влажности почвы. Схожий подход был применен в работе [22] для глобальной модели динамики растительного покрова, в которой определенная по спутниковым данным входящая радиация (FPAR) ассимилировалась в модель для определения доли поверхности, занятой растительностью. Аналогичный подход также применялся для моделирования развития природных пожаров в работе [25], в которой для ассимиляции использовались регулярно обновляемые данные о температуре кромки горения.
Например, в работе [23] входные параметры физической модели развития пожаров были оптимизированы по данным о периметре пожара для увеличения точности моделирования. Еще одни пример параметризации математической модели распространения пожара приведен в работе [119]. В ней спутниковые данные о приросте площади пожара использовались для определения параметров модели, воспроизведения возможного его развития и определения момента начала тушения и его интенсивности.
Также данные спутникового мониторинга могут использоваться для параметризации моделей наземных экосистем с помощью методов оптимизации. Методы оптимизации находят оптимум (максимум/минимум) некоторой функции, варьируя значение ее параметров по заданному правилу. Для моделей растительного покрова функция - это один «прогон» модели, параметры функции - оптимизируемые параметры модели и значения функции - некоторый индикатор качества модели. Существует несколько возможных подходов к классификации методов оптимизации. В первую очередь их можно разделить по тому, осуществляют ли они локальный или глобальный поиск оптимума.
Локальные методы оптимизации обычно осуществляют поиск в некоторой малой области, приближаясь к находящемуся в этой области локальному оптимуму, игнорируя точки за пределами этой области. Такая область иногда называется областью притяжения локального оптимума. Эта группа методов может найти глобальный оптимум для определенных стартовых точек и функций (например, если у функции один экстремум). Для поиска локальных оптимумов часто используются метод градиентного спуска, метод Ньютона или квазиньютоновские методы, метод Гаусса и др. Стоит отметить, что для выпуклых функций задача локальной оптимизации оказывается тождественна задаче глобальной оптимизации. Так как модели растительности имеют сложную природу, то невозможно гарантировать форму функции качества для оптимизируемой модели, что ограничивает возможность использования данной группы методов.
Поиск глобального оптимума для функций общего вида (не выпуклых, с множеством экстремумов) является более сложной задачей. В общем случае не существует методов, которые гарантированно могут найти оптимальное значение функции за ограниченное время. Существует несколько работ, посвященных общему описанию глобальных методов оптимизации, например книги [120], [121]. Методы глобальной оптимизации можно разделить на рациональные и эвристические. Рациональные методы исходят из предположений о форме оптимизируемых функций, что позволяет им построить наиболее эффективный для данного вида функций алгоритм оптимизации, способный гарантировать нахождение глобального оптимума для данной функции. Примеры рациональных методов оптимизации можно найти в обзоре [122]. Как уже было указано ранее, ввиду невозможности определения формы оптимизируемой функции в задаче параметризации модели, применимость таких методов ограничена.
Детерминированная и стохастическая модель прогнозирования динамики природных пожаров
Предварительная настройки параметров модели и доработка ряда ее модулей позволили существенно улучшить качество моделирования пространственного распространения типов растительности. Но стоит отметить, что значения параметров, полученные в разделе 2.1, могут являться неоптимальными. Также в процессе модификации модели были введены новые параметры, значения которых выбирались произвольно.
Для повышения точности работы модели была проведена региональная оптимизация ее параметров, наиболее существенным образом влияющих на пространственное распределение типов растительности. При выборе подлежащих оптимизации параметров модели предпочтение отдавалось параметрам, отличающимся простотой интерпретации и трудностью непосредственной оценки ввиду нечеткости физического смысла. В модели имеется несколько такого рода параметров, например, параметры эмпирических ограничений на температуру воздуха, при которых в растительности могут происходить процессы, необходимые для существования и размножения данного типа. Параметры уравнений фотосинтеза, эвапотранспирации, водного баланса и других аналогичных модулей не включались в процедуру формальной оптимизацию в силу хорошей их интерпретируемости из физических и химических соображений, возможности непосредственного определения объективными методами, а также ввиду их неочевидного влияния на пространственное распределение типов растительного покрова. Кроме того, при выборе оптимизируемых параметров учитывались результаты предварительно проведенной оценки чувствительности критерия качества моделирования к независимому варьированию их значений. С учетом приведенных выше соображений был выбран список из 12 параметров модели, девять из которых описывают климатические условия для различных типов растительности, при выходе за границы которых они не могут размножаться или погибают. Кроме того, использовались параметры модели, характеризующие площадь листовой поверхности для лиственничных лесов, коэффициент в формуле конкуренции за свет и зависимость температуры от высоты над уровнем моря. Два последних параметра были выбраны в связи с тем, что их исходные значения были заданы произвольно на этапе модификации модели SEVER.
Оптимизации параметров модели была выполнена в два этапа разными методами. На первом этапе был использован эвристический метод глобального поиска оптимума, который, для ускорения, использовал выборочную оценку точности модели. Затем для модели с полной оценкой точности был осуществлен поиск локального оптимума, в качестве стартовой точки которого использовался найденный на предыдущем шаге глобальной оптимум. Для реализации обоих этапов оптимизации использовался язык R [135].
На первом шаге оптимизации нахождение глобального оптимума модели выполнялось с использованием метода EGO (Efficient Global Optimisation) [128], реализованного в языке R в составе пакета DiceOptim [136]. Указанный метод сочетает поиск оптимального значения параметров с исследованием всего пространства параметров с помощью метода аппроксимации кригинг [137], заменяющего аппроксимируемую функцию суммой полиномиальной и случайной компонент. Кригинг в точности интерполирует исходную функцию в точках, по которым построена аппроксимация и, в силу стохастической природы, может предоставить оценку среднеквадратического отклонения аппроксимации в любой точке пространства параметров. Сначала алгоритм EGO, на основе набора исходных точек, строит аппроксимацию, и находит ее оптимум для значения критерия ожидаемого улучшения (Expected Improvement, EI) в виде: EI(x) = (fmm - у)Ф(/тт У) + 8ф(/тт У) S S где /шп - минимальное значение функции, найденной на данный момент, у - значение функции в х, s- ошибка (отклонение) аппроксимации в точке х, Ф и ф - нормальная функция распределения и плотность нормального распределения соответственно. Данный критерий увеличивается, если значение функции в точке близко к минимальному, найденному на данный момент, или меньше его (первое слагаемое) и ошибка аппроксимации (отклонение s) в новой точке велика (второе слагаемое).
После нахождения точки, дающей максимальное значение критерия ожидаемого улучшения, новая точка проверяется по исходной функции, и аппроксимирующая функция обновляется. Итерации повторяются до тех пор, пока улучшение значения критерия не достигнет предопределенного порогового значения. Такая структура метода делает его быстрым (за счет поиска оптимума по аппроксимации) и эффективным для глобальной оптимизации (из-за специфической формы критерия).
Эвристические методы глобальной оптимизации, подобные методы EGO, обычно требуют значительное количество вычислений оптимизируемой функции (выполнений модели) для определения глобального оптимума. Так как время работы модели для всей территории России может составлять несколько часов, то полное время поиска глобального оптимума модели может составить более месяца. В связи с этим на первом этапе оптимизации использовалась выборочная оценка качества работы модели.
При выборочной оценке точности модели моделирование выполнялось для небольшой (порядка 5%) части клеток всей территории России, а оценка качества моделирования строилась по этим клеткам так же, как и для полного набора клеток. Сравнение значений критерия качества модели, полученной с помощью выборочной и полной оценок показало, что они имеют существенное отклонение примерно на 10%, но при этом величина коэффициента детерминации составила 0,88. Высокий уровень корреляции между значениями критерия качества моделирования при использовании различных подходов оценки может служить обоснованием замены метода оценки точности при исследовании пространства параметров модели. Однако, в силу того, что значения критериев для двух подходов различны, оптимум для выборочной оценки качества модели может не совпадать с оптимумом для полной оценки точности модели.
Таким образом, найденный на первом этапе глобальный оптимум модели может на самом деле не являться даже локальным оптимумом качества модели, что приводит к необходимости проведения второго этапа оптимизации модели. На втором этапе оптимизации осуществляется поиск локального оптимума модели с помощью квази-ньютоновского алгоритма BFGS.
Была использована реализация метода BFGS (Broyden, Fletcher, Goldfarb, Shanno) в функции optim() стандартного пакета stats языка R. Метод BFGS -это широко известный квази-ньютоновский алгоритм оптимизации, использующий градиент оптимизируемой функции (вычисляемый напрямую) и ее Гессиан (который аппроксимируется по ранее пройденным точкам функции). Этот алгоритм изменяет значения параметров функции в направлении уменьшения градиента, также используя данные о выпуклости (вогнутости) исходной функции (Гессиан). В данном случае информация о градиенте модели отсутствовала, поэтому была использована конечная аппроксимация градиента. Этот метод оценки градиента для модели требует существенного времени на выполнение, поэтому второй шаг оптимизации включал небольшое число итераций.
Примеры практической апробации LAGMA-PLUS в технологиях оценки наземных экосистем
Моделирование динамики наземных экосистем невозможно без актуальной информации об их состоянии и условиях окружающей среды. В последние годы регулярное поступление такой информации для больших территорий стало возможным благодаря методам дистанционного зондирования Земли из космоса. Но объем этих данных и требование регулярности обновления получаемой на их основе информации о земном покрове приводят к необходимости разработки автоматизированных методов, обеспечивающих возможность единообразной обработки данных для больших территорий. В данной работе было разработано ПО локально-адаптивной классификации и оценивания характеристик земного покрова LAGMA-PLUS, обеспечивающее возможность ежегодного спутникового картографирования наземных экосистем на больших территориях.
Одноименный метод LAGMA, лежащий в основе данного ПО, предназначен для решения проблемы пространственной изменчивости спектрально-отражательных характеристик земного покрова на больших территориях. Эта проблема часто встречается при картографировании больших территорий [12, 13, 82], ее решение возможно с помощью стратификации или посредством разработки альтернативных методов оценки параметров растительности (например, гиперкластеризация в задачах картографирования). Но существующие подходы к решению проблемы пространственной изменчивости обладают недостатками, мешающими их применению для регулярной оценки характеристик растительности на больших территориях (см. главу 1).
Локально адаптивный метод LAGMA (locally adaptive global mapping algorithm) предоставляет новый подход к решению проблемы пространственной изменчивости спектрально-отражательных характеристик растительности. Данный алгоритм был разработан в ИКИ РАН для решения задачи картографирования растительного покрова России [143]. В основе алгоритма лежит принцип локализации обучающей выборки, предполагающий, что для классификации в каждой точке используется находящаяся в ее локальной окрестности часть обучающей выборки.
Исходный метод LAGMA [143] позволил решить задачу картографирования земного покрова с помощью классификации методом максимального правдоподобия. Была проведена доработка метода LAGMA, позволяющая интегрировать в него другие методы классификации и расширить механизм обеспечения локальной адаптивности на решение задач оценивания характеристик растительного покрова, представленных в непрерывных шкалах. Данная работа и ее результаты опубликованы в научных статьях [150, 151] и описаны в главе 4 данной диссертационной работы.
Для описания метода LAGMA сформулируем проблему определения характеристик растительности по спутниковым данным в общем виде. Предположим, у нас есть w-мерное пространство параметров, полученных по данным ДЗЗ F = {(/b/2,...,/„)} где ft,i = \,...,n - это значения отдельных параметров. Существует некоторая интересующая характеристика С, которая может быть непрерывной ли дискретной, например, обозначать параметры растительного покрова (LAI, NPP, биомасса) или типы земных покровов. Также существует неизвестная функция А : F — С, которая задает отношение между множеством параметров и возможными значениями характеристики. Предположим, что для некоторого подмножества пространства параметров (обучающей выборки) FT F известны соответствующие им значения характеристики, что можно выразить следующим соотношением: KNOWN : FT - С. Также предположим, что существует некоторый метод, который позволяет на основании знаний об известных значениях характеристик и значениях параметров построить приближение к реальной функции A: С. Обозначим этот метод TRAIN :{F}x {KNOWN} {A}. Функция TRAIN зависит от решаемой задачи. Например, при решении задачи классификации TRAIN представляет собой процесс построения классификатора по обучающей выборке. В случае, если С является непрерывной величиной, то метод TRAIN может состоять в построении регрессии по известным зависимостям между спутниковыми параметрами и характеристикой. В случае, если KNOWN: FT - С является системой локализованных отношений (например, выработанных на разных тестовых участках) и эти отношения можно расширить на все пространство спутниковых параметров, то A может состоять в осреднении значений, даваемых каждой зависимостью (возможно, взвешенных по расстоянию от тестовых участков до исследуемой территории).
Основная идея метода LAGMA - создание локальной приближенной функции AL, применяемой к некоторой локальной области и построенной по части подмножества FT, пространственно близкой к этой локальной области. Для того, чтобы часть подмножества FT, используемая для построения AL, могла репрезентативно представлять весь диапазон характеристик С, этот диапазон можно представить как сумму диапазонов С = Ycj. Например в i=l,...Jc задаче классификации набор {сх} может быть интерпретирован как отдельные классы. Разбиение зависит от задачи и в отдельных задачах может не производиться (к = 1).