Содержание к диссертации
Введение .. 3
Глава I. О ВЕРХНИХ ПОЛУРЕШЕТКАХ РЕКУРСИВНО-ПЕРЕЧИСЛИМЫХ СТЕПЕНЕЙ ТАБЛИЧНОГО ТИПА
I. Сводимости табличного типа и счетчики 21
2. О минимальных степенях 32
3. oTk{LM)JULc)nl^Lt) 44
4. оТОД^)и"ТСсЦіО 57
5. oT(Lp) и~П(Іасі) 64
Глава 2. СООТНОШЕНИЯ МЕЖДУ ПОЛНЫМИ МНОЖЕСТВАМИ
6. Предварительные результаты 75
7. Основная лемма 81
8. О М-полных множествах 87
9. Об С-полных множествах 92
Глава 3. СООТНОШЕНИЯ МЕВДУ СТЕПЕНЯМИ
10. О Шг и I степенях внутри tt-степени 101
II. Об уп- степенях внутри \г степени 109
12. Об т-степенях внутри ^тх-степени 115
13. Об одной гипотезе Ю.Ершова 125
Глава 4. ОБ 1- И ПЧ-СВОДИМОСТИ
14. Об {-степенях внутри m-степени 132
15. Один пример решетки LcX) 142
16. Три теоремы об Wi-степенях 151
17. Разрешимость V3-теории LM 162
Литература 167
Введение к работе
Теория алгоритмов (рекурсивных функций) является одним из современных и бурно развивающихся разделов математической логики. Её появление обусловлено формализацией в середине 30-х годов интуитивного понятия вычислимой функции. Важным моментом этой теории является рассмотрение и классификация подмножеств множества натуральных чисел 14 = -(0,1,2,,..} с алгоритмической точки зрения, а также исследование структур, возникающих в результате такой классификации. Для каждого множества A , As N, можно сформулировать следующую проблему: существует ли алгоритм, позволяющий для любого Х fsl ответить на вопрос о принадлежности X к А. Множества, для которых данная проблема разрешима, были названы рекурсивными. Однако скоро выяснилось, что существуют различные по своей "сложности" рекурсивно перечислимые (р.п.) множества, не являющиеся рекурсивными, которые стали особым объектом изучения. Инструментом для классификации подмножеств N по их "сложности" служит понятие сводимости, являющееся одним из центральных в теории алгоритмов. На интуитивном уровне множество А сводимо к множеству D , если существует алгоритм, который решал бы проблему вхождения элементов для А при условии, что есть возможность пользоваться информацией о принадлежности тех или иных элементов множеству В . Такая сводимость в самом общем виде называется тьюринговой ( І-) сводимостью.
_ 4 -
Результаты и методы теории алгоритмов быстро нашли своё применение в различных областях математики. Выяснилось, что многие из известных проблем являются неразрешимыми. Такими будут, например, проблема распознавания тождественной истинности формул исчисления предикатов, проблемы тождества слов конечно определённых групп и полугрупп, 10-я проблема Гильберта и другие. Часто неразрешимость одной проблемы доказывается как раз посредством сведения к ней другой, о которой заранее известно, что она неразрешима. Эта последняя проблема в большинстве случаев является проблемой разрешимости подходящего р.п. множества.
Наряду с I -сводимостью для исследования множеств уже в 1944
году Э.Пост [зз] ввёл некоторые специальные виды сводимостей -
такие, как m-сводимость, табличная (tt~) и ограниченная таб
личная сводимости. Именно, множество Л кп-сводимо к
множеству В (А^Е>), если существует всюду определённая на Л/
вычислимая функция т такая, что для всех
. Множество A tt -сводимо к , если существует
алгоритм, который для каждого XN даёт набор чисел ^и^^ч'Лхкя} и булеву функцию fytyifyiy.tyn^Tawe, что
где jfC't)- 1? если . В част-
ности, если П(Х) для всех Х не больше некоторого фиксированного числа, то говорят, что А \>Х1-сводимо к D (.А ^^ЦО), Ясно, что Пг\-сводимость - частный случай Ъи-сводимости, которая в свою очередь является частным случаем tt-сводимости. Вообще R„~сводимость слабее Г-сводимости, если А ^ГВ влечёт
A^RE> дмве« A,E>cis|, A,B{0,nI}.
От произвольной сводимости Y- на подмножествах N по крайней мере требуют, чтобы отношение 4.г было бы предпорядком.
- 5 -Если положить
то =г будет являться отношением эквивалентности, отдельный класс которой называется Т-степеньго (и р.п. Y-степенью, если ей принадлежит р.п. множество). На множестве всех (или только р.п.) Y-степеней естественным образом также определяется отношение частичного порядка ^ r, вместе с которым оно образует верхнюю полурешетку, как только V- сводимость слабее т-своди-мости. В этом случае верхнюю полурешетку р.п. г-степеней будем обозначать через Ллг , а её элементарную теорию через Хорошо известно [4], что все эти полурешетки имеют наименьший элемент О и наибольший элемент 11 .Р.п. множества, принадлежащие наибольшей Y-степени 11 полурешетки Lxv , называются
Т- полными.
Сводимости, промежуточные по своей силе между ТУХ- и tt-сводимостью, называются сводимостями табличного типа (иногда сильными сводимостями). Наиболее прямолинейным способом получения какой-либо сводимости табличного типа является требование, чтобы булева функция Вх , участвующая в определении tt-сводимости, принадлежала для всех X некоторому замкнутому классу булевых функций. В частности, этот класс, соответствующий 171-сводимости ( и-сводимости), есть {%\ (класс всех булевых функций). Именно таким образом постепенно были определены и начали исследоваться дизъюнктивная (QM, конъюнктивная Со ) , позитивная (D-) , ott;[ и линейная ((.") сводимости. Как выяснилось [5], по этому пути новых сводимостей получить нельзя, и поэтому перечисленные выше семь сводимостей естественно назвать основными. В то же время по аналогии с ЫХ-сводимостью можно определить и другие ограниченные сводимости табличного типа, такие, как U; к; Ар-,
Шг и YVt-сводимость. Однако они фактически не изучались и за-
- б -
нимают пока среди других сводимостей второстепенное место. Кроме' того, 0ТЦ~ и іпа-сводимость на р.п. множествах совпадают с т-сводимостью и поэтому ниже не рассматриваются. Главное внимание в диссертации будет уделено классу основных сводимостей вместе с снТ-сводимоетью - наиболее важной и интересной из ограниченных сводимостей, то есть классу
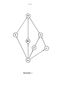
3t- {ttt-.tt-.l-.p-.d-.c-.m-V
Соотношения между этими сводимостями по силе указаны на диаграмме I.
К началу 70-х годов "tt-сводимость (и другие сводимости табличного типа) по сравнению с |- и ГП-сводимостыо оказалась наименее изученной. Это, по-видимому, объясняется тем, что понятие
it-сводимости не отличается такой простотой, как щп-сводимости, и такой общностью, как понятие |-сводимости. Более того, её свойства существенно отличаются от свойств |- и ЩП-сводимости, что потребовало от её исследователей привлечения новых идей и методов. В то же время в изучении различных сводимостей явно выделились три направления. Одно из них, наиболее раннее, заключается в том, чтобы охарактеризовать Y-полные множества и выяснить соотношения, например, по включению, между классами Y-полных множеств для тех или иных сводимостей **-. Другое связано с вопросами строения полурешеток Г-степеней, в особенности р.п.
К"- степеней. Третье - с вопросами, сколько Y-степеней имеется и как они расположены в степенях, относительно более слабой сводимости, Именно решению трёх проблем для класса сводимостей сгі, относящихся к этим трём направлениям, а также некоторым естественным вопросам, примыкающим к ГО-сводимости, посвящена настоящая диссертация.
Перейдём к более подробному изложению результатов. Диссертация состоит из введения, четырёх глав, объединяющих семнадцать
tt-
m-
Диаграмма I
параграфов, и списка цитируемой литературы.