Содержание к диссертации
Введение
1. Современное состояние проблемы обеспечения работоспособности стяжных соединений редукторов и шестеренных клетей в главных линиях прокатных станов 8
1.1. Особенности конструкций и редукторов и шестеренных клетей трансмиссий главных приводов прокатных станов 8
1.2. Существующие методы расчета редукторов и шестеренных клетей главных приводов прокатных станов 15
Выводы по главе 1 36
2. Теоретическое исследование процесса формирования динамических нагрузок в двухвалковой шестеренной клети главной линии прокатного стана 38
2.1. Описание геометрических параметров, характеризующих взаимодействие шевронных зубчатых колес 38
2.2. Описание силового взаимодействия колес в зубчатом зацеплении 77
2.3. Описание силового взаимодействия зубчатого колеса с корпусными и крепежными деталями 108
2.4. Динамическая модель нагружения главной линии листового стана 125
3. Экспериментальное исследование динамических процессов в элементах главной линии и разработка мероприятий, обеспечивающих работоспособности двухвалковых шестеренных клетей 130
3.1. Разработка устройств, обеспечивающих тарированную затяжку корпусов и крышек шестеренных клетей 130
3.2. Методика проведения экспериментальных исследований динамических процессов в элементах главной линии прокатной клети 134
3.3. Результаты экспериментальных исследований динамических процессов в элементах главной линии прокатной клети 141
3.4. Сравнение результатов экспериментальных исследований с результатами расчетов динамических
переходных процессов 152
3.5. Разработка рекомендаций, обеспечивающих стабилизацию работы стяжных узлов в шестеренных клетях широкополосных станов горячей прокатки 155
4. Основные результаты и выводы 159
Список литературы 163
Приложение 167
- Существующие методы расчета редукторов и шестеренных клетей главных приводов прокатных станов
- Описание силового взаимодействия зубчатого колеса с корпусными и крепежными деталями
- Динамическая модель нагружения главной линии листового стана
- Методика проведения экспериментальных исследований динамических процессов в элементах главной линии прокатной клети
Введение к работе
Работоспособность элементов главных линий листовых станов горячей прокатки существенно зависит от динамических нагрузок, формирующихся при захвате заготовки рабочими валками прокатной клети. В значительной мере это относится к высокомоментным двухвалковым шестеренным клетям, входящих в состав главных линий черновых клетей непрерывных широкополосных станов горячей прокатки. Практика эксплуатации ряда прокатных станов выявила неудовлетворительную работоспособность зубчатого зацепления шестеренных валков, стяжных соединений крышек и корпусов шестеренных клетей.
Основными причинами недостаточной работоспособности шестеренных клетей являются действующие в них динамические нагрузки и неудовлетворительная предварительная затяжка корпусных деталей. При неправильной предварительной затяжке стяжных шпилек в процессе нагружения шестеренной клети может происходить раскрытие стыков. Это приводит к появлению ударных нагрузок при закрытии стыков и ухудшению условий работы подшипников и зубчатых зацеплений шестеренных валков. В дополнение к этому развиваются остаточные деформации в резьбовом соединении шпилек, что приводит к дальнейшему ослаблению стягиваемых стыков и увеличению ударных нагрузок при закрытии стыков. Кроме того, из-за утечек через стык увеличивается расход масла в системе смазки шестеренной клети или редуктора. В ряде случаев неправильная затяжка может привести к возникновению в резьбовых соединениях шпилек недопустимо высоких напряжений, а также привести к увеличению циклической составляющей нагрузок, вызывающей их усталостное разрушение.
Для увеличения работоспособности высокомоментных шестеренных клетей необходимо располагать информацией о нагрузках, действующих на элементы корпуса шестеренной клети, подшипниковые опоры, зубчатое зацепление и стяжные шпильки при различных режимах прокатки. Для этого необходимо провести исследование нагрузок, действующих в элементах главной линии, как при установившемся процессе прокатки, так и в динамических режимах, связанных с захватом металла валками прокатной клети. При этом следует отметить, что традиционные методики оценки динамических нагрузок, действующих в стыках между корпусом и крышкой шестеренной клети, не учитывают колебательного движения цапф шестеренных валков в пределах радиальных и осевых зазоров подшипников, которое приводит к дополнительному росту нагрузок в стяжных шпильках.
Для обеспечения требуемых сил затяжки необходима также разработка мероприятий и устройств, позволяющих контролировать силу предварительной затяжки стяжных шпилек при сборке шестеренной клети. При использовании традиционных методов затяжки стяжных шпилек шестеренных клетей вследствие неопределенности трения в резьбе и на торце гайки силы в стяжных шпильках после затяжки могут существенно отличаться как между собой, так и от требуемого значения.
В связи с этим проблема определения динамических нагрузок, действующих главных линиях листовых станов горячей прокатки, включая зубчатые передачи и корпусные детали шестеренных клетей и необходимого уровня предварительной затяжки шпилек, стягивающих крышки и корпуса шестеренных клетей, а также разработка устройств, позволяющих обеспечить этот уровень предварительной затяжки, является актуальной.
Цели и задачи работы:
На основании теоретических и экспериментальных исследований определить уровень динамических нагрузок, действующих в главной линии листового стана горячей прокатки, включая зубчатое зацепление и корпусные детали шестеренной клети.
Определить уровень предварительной затяжки стяжных шпилек, при котором в процессе эксплуатации будет соблюдаться условие нераскрытия стыка между крышкой и корпусом шестеренной клети.
Разработать новые конструкции стяжных шпилек и устройств, обеспечивающих: во-первых, получение необходимого уровня сил
предварительной затяжки шпилек и во вторых, стабильность сил
/
предварительной затяжки шпилек в течение срока эксплуатации между капитальными ремонтами шестеренной клети.
Для достижения этих целей были поставлены и решены следующие задачи:
Разработка математической модели, позволяющей расчетным путем определить закономерности формирования динамических нагрузок в элементах главной линии прокатного стана, включая зубчатое зацепление, шпильки и стыки стяжных соединений крышек и корпусов шестеренных клетей.
Определение уровня сил предварительной затяжки стяжных шпилек, при которых будет соблюдаться условие нераскрытия стыка между крышкой и корпусом шестеренной клети при действии динамических нагрузок.
Экспериментальная проверка разработанной математической формирования динамических нагрузок на действующем оборудовании.
Совершенствование конструкции стяжных шпилек и разработка устройств, позволяющих осуществить тарированную затяжку стяжных шпилек на действующих шестеренных клетях.
Научная новизна.
Математически описаны и экспериментально подтверждены закономерности формирования динамических нагрузок в главной линии листового стана горячей прокатки, включая зубчатое зацепление, корпусные и крепежные детали двухвалковых шестеренных клетей.
Практическая ценность.
На основе разработанной математической модели определены уровни сил предварительной затяжки стяжных шпилек, при которых соблюдается условие нераскрытия стыков между крышкой и корпусом шестеренной клети в условиях действующих динамических нагрузок.
Разработаны и изготовлены новые стяжные шпильки и гидравлические устройства, позволяющие осуществить тарированную безмоментную затяжку стяжных шпилек.
Выполнена тарированная затяжка новых стяжных шпилек на шестеренной клети 1400 черновой группы стана 2000 АО «Северсталь» и на шестеренной клети 1300 черновой группы стана 2000 Новолипецкого металлургического комбината.
Апробация работы.
Основные результаты работы докладывались и обсуждались на Всероссийской конференции молодых ученых и специалистов «Будущее машиностроения России» в ноябре 2008 г.
Публикации.
По материалам диссертации опубликовано 7 статей.
Существующие методы расчета редукторов и шестеренных клетей главных приводов прокатных станов
В существующих методиках расчета редукторов и шестеренных клетей главных приводов прокатных станов [14, 29, 32] основное внимание уделяется геометрическому и прочностному расчету зубчатого зацепления. В настоящее время для расчета зубчатого зацепления в основном используется ГОСТ 21354-87 [9]. Существует относительно немного работ, посвященных расчету корпусных и крепежных редукторов и шестеренных клетей трансмиссий главных приводов, в которых учитывается специфика нагружения и эксплуатации прокатных клетей.
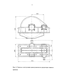
Например, для определения необходимого размера болтов, крепящих корпус шестеренной клети к фундаменту, производится расчет шестеренной клети на опрокидывание. Принципы этого расчета изложены в работах [14, 29, 32]. На рис. 1.4 приведена схема для расчета опрокидывающего момента, действующего на шестеренную клеть. Эта схема соответствует конструкции шестеренной клети, в которой приводным является нижний шестеренный валок. Со стороны двигателя или редуктора на нижний шестеренный валок через упругий вал действует момент М№ . Со стороны шпинделей на нижний шестеренный валок действует момент Мх, а на верхний шестеренный валок действует момент М2. Как правило один из этих моментов будет положительным, а другой отрицательным. При равномерном распределении моментов прокатки между верхним и нижним прокатными валками выполняется следующее условие - М, = -М2. В этом случае опрокидывающий момент МОПР определяется по следующей зависимости:
В работах [14, 29, 32] приведены также случаи, когда один из моментов (Мх или М2) равен нулю. В рассматриваемой конструкции с приводным нижним шестеренным валком наибольшее значение опрокидывающий момент принимает, в такой ситуации, когда действующий на нижний шестеренный валок момент Ых равен нулю. В этом случае момент, создаваемый прокатываемым металлом на верхнем прокатном валке и прикладываемый к верхнему шестеренному валку, равен полному моменту прокатки, то есть М2 - Мпр. В отмеченных работах рассматривается статическое равновесие шестеренных валков. В связи с этим крутящий момент Мх,, передаваемый со стороны привода на нижний шестеренный
Расчет опрокидывающего момента по зависимостям (1.1), (1.2) и усилия в фундаментном болте по зависимости (1.3) производится с учетом действия статического момента прокатки на прокатных валках. Однако в линии привода прокатной клети в переходных режимах работы формируются динамические нагрузки, которые могут значительно превышать статические моменты прокатки. Если не учитывать действующие динамические нагрузки, то расчетная сила 0Б затяжки фундаментного болта может оказаться меньше силы, необходимой для обеспечения отсутствия раскрытия стыка между корпусом шестеренной клети и фундаментом. Достаточно подробно проблемы формирования динамических нагрузок в фундаментных болтах, крепящих корпус редуктора главного привода прокатной клети к фундаменту, рассмотрены в работе [2]. В соответствии с этой работой на рис. 1.5 приведена расчетная схема системы вращающихся масс главного привода, а на рис. 1.6 приведена расчетная схема редуктора главного привода и схема его крепления к фундаменту. В расчетной схеме, приведенной на рис.1.5 введены следующие обозначения
Описание силового взаимодействия зубчатого колеса с корпусными и крепежными деталями
Для определения сил взаимодействия необходимо рассмотреть возможность деформации поверхностей зубьев в точках контакта. В соответствии с 2.1 математическая модель контакта должна предусматривать возможность взаимодействия между зубчатыми колесами, оси вращения которых могут быть непараллельными. В этом случае необходимо рассмотреть взаимодействие кромок боковых поверхностей зубьев зубчатого колеса К2 с передней и задней поверхностью зубьев зубчатого колеса Кх . При том условии, что зубья колес Кх и К2 находятся в зацеплении, передняя поверхность /-го зуба левого полушеврона колеса Кх будет находиться в контакте с наружной боковой кромкой передней поверхности ]-го зуба левого полушеврона колеса К2. Для того чтобы определить эти точки контакта необходимо приравнять правые части уравнений (2.26) и (2.59). В результате мы получим систему трех уравнений. Неизвестными в этой системе уравнений являются независимые параметры и\ои, \ \пи, к20щ. Решение будет также зависеть от известных параметров, входящих в уравнения (2.26) и (2.59). Перечислим эти параметры: Из ограничений, накладываемых на независимые параметры, можно будет также определить номера зубьев на колесах, которые контактируют в данный момент времени. Кроме того, для определения сил взаимодействия необходимо предусмотреть возможность деформации поверхностей и кромок в точках контакта. При этом также необходимо сформулировать модель деформирования и формирования сил в точках контакта. В результате процедура решения получается достаточно трудоемкой. Процесс решения можно существенно упростить, если учесть тот факт, что в эвольвентном зацеплении точки контакта между зубьями колеса Кх и колеса К2 лежат на линии зацепления. В соответствие со сформулированными выше допущениями эта линия зацепления является общей касательной к поверхности основного цилиндра колеса Кх и основной окружности зубчатых кромок колеса К2. Кроме того, эта линия зацепления и нормаль к ней лежат в плоскости кромки зубьев колеса К2 параллельной плоскости Х0О0У.
Схема для определения координат точек, в которых происходит контакт наружной кромки передней поверхности зуба левого полушеврона колеса К2 с передней поверхностью зуба левого полушеврона зубчатого колеса Кх, представлена на рис.2.8а. В соответствии с этой схемой и зависимостью (2.67) можно определить межосевое расстояние в рассматриваемом зацеплении: Угол между прямой, представляющей это межосевое расстояние и плоскостью X0OZ равен: В соответствие со схемой приведенной на рис.2.8а определим угол между нормалью к линии зацепления передних поверхностей зубьев, рассматриваемой наружной кромки левого полушеврона, и плоскостью X0Z в неподвижной системе координат O0XY0Z: Угол между нормалью к линии зацепления задних поверхностей зубьев (рис.2.9а), рассматриваемой наружной кромки левого полушеврона, и плоскостью X0OZ в неподвижной системе координат O0X0Y0Z: Как видно из уравнения (2.78) значение определяемого независимого параметра и\ш при известных значениях м ош, у/я, срш, зависит от номера / зуба колеса. Номер / зуба колеса Кх, который может вступить в контакт с зубом колеса К2 можно определить из (2.78) с учетом ограничений (2.4), накладываемых на величину параметра и\ои. При определении номеров зубьев, входящих в контакт, необходимо конкретизировать величину и0, , представляющую собой угол между плоскостью Хх0х2[ и осью 1-го зуба в сечении плоскостью Х О Г1.
Положим итр =0. Из (2.78), подставив в него и\пи = м1тах, можно определить максимальный номер зуба ОШтяк колеса Кп находящегося в зацеплении с зубом колеса К2: где п ...) означает целую часть от действительного числа, стоящего в скобках. Учитывая введенную нумерацию зубьев на рассматриваемых зубчатых колесах и особенности эвольвентного зацепления для определения минимального номера зуба гОШха{а, колеса Кх, находящегося в зацеплении, необходимо рассмотреть на колесе К2 номера зубьев наружная боковая кромка левого полушеврона лежит на линии зацепления. На рис 2.86 представлена соответствующая геометрическая схема. Для того чтобы определить координаты точек пересечения кромок зубьев колеса К2 с линией зацепления, определяемой углом п 1)[И, воспользуемся уравнениями (2.59а), положив в них: Из (2.80) и (2.59а) можно определить значение независимого параметра Как видно из уравнения (2.81) значение определяемого независимого параметра и2Шг при известных значениях м ти, ср202, зависит от номера / зуба колеса. Номер / зуба колеса К2, который может вступить в контакт с зубом колеса Кх можно определить из (2.81) с учетом ограничений (2.38), накладываемых на величину параметра и\й1]. При определении номеров зубьев, входящих в контакт, необходимо конкретизировать величину ит р, представляющую собой угол между плоскостью Х202Х2 и осью 1-го зуба в сечении плоскостью Х202У2. Положим щ2 р = л + 0,5и22 . В дальнейшем движение мы будем рассматривать вращение пары зубчатых колес начиная с такого исходного положения зубчатых колес, при котором р10г = д 207 = 0 . В этом случае при принятых значениях иоир = 0, щ2(р = л + 0,5и22 и плотном зацеплении передние поверхности /-ого зуба колеса Ку будут касаться передних поверхностей / - ого зуба колеса К2, то есть получим соотношение
Динамическая модель нагружения главной линии листового стана
Время взаимодействия зубьев в процессе их соударения существенно меньше, чем время, за которое формируется динамическая нагрузка в шпинделе, передающем крутящий момент или в стягивающих корпус и крышку шестеренной клети шпильках. При этом величина контактных сил, возникающих при соударении зубьев, не является предметом рассмотрения в данной работе, а основной задачей разрабатываемой математической модели является определение динамических нагрузок именно в стяжных шпильках и шпинделе. Такая ситуация характерна при рассмотрении удара, когда взаимодействие определяется величиной импульса, а величина силы взаимодействия при этом не рассматривается. Так как время взаимодействия при соударении зубьев зависит от параметров жесткости ср и вязкости Ьр, то в этом случае нам достаточно иметь ориентировочные оценки величин сР и V
Величину коэффициента жесткости сР можно оценить, рассматривая изгиб зуба как изгиб консольной балки с приложенной на консоли силой . При этом размеры балки определяются характерными геометрическими параметрами зуба (рис,2.11а). Ширина балки равняется половине ширине Вн полушеврона. С учетом схемы нагружения жесткость ср равна: где Е модуль упругости материала рассматриваемой балки.
Оценку коэффициента Ьр вязкого сопротивления будем делать с учетом принятой нами модели упруго-вязкого взаимодействия шестеренных валков. Для этого воспользуемся понятием коэффициента к восстановления скорости при соударении тел [35]. Как отмечено в [35], коэффициент восстановления в определенной мере зависит от формы соударяющихся тел и соотношения их масс, однако в расчетах обычно принимают, что коэффициент восстановления зависит только от материала соударяющихся тел.
Для того, чтобы дать оценку числового значения Ър рассмотрим расчетную схему (рис.2.116), в соответствии с которой в точке приложения к зубу силы Р имеется масса тв, движущаяся с начальной скоростью /0. Обозначим через й перемещение массы тн. В процессе соударения величина с! перемещения массы тв изменяется от 0 до й?тах, а затем изменяется от с1тях до 0. В момент возвращение массы тв в исходное положение ее скорость равна с1х. Отношение скоростей представляет собой коэффициент восстановления скорости [35].
Коэффициент восстановления скорости к также характеризует рассеяние энергии при соударении тел, в соответствии с которым можно оценить величину коэффициента ЪР вязкого сопротивления. Для этого примем допущение о том, что модуль скорости массы тв зависит линейно от перемещения d . При изменении перемещения от 0 до dm3K модуль скорости d массы тв изменяется от d0 до 0, а при обратном перемещении от dmax до О модуль скорости массы тв изменяется от 0 до dx. Суммарная сила Q, действующая со стороны упругого элемента сР на массу На рис. 2.11в представлена зависимость изменения силы О в процессе роста деформации d (траектория 1) и в процессе уменьшения деформации d (траектория 2). Траектория 3 представляет собой упругую составляющую суммарной силы Q. Заштрихованная площадь на рис.Пв соответствует величине энергии AT рассеянной в упругом элементе сР в процессе соударения. И эта же величина AT равна разности кинетических энергий массы тв в начале и в конце процесса соударения:
Методика проведения экспериментальных исследований динамических процессов в элементах главной линии прокатной клети
На крышку шестеренной клети кроме сил, действующих со стороны левого и правого подшипника, действует также силы со стороны стяжных шпилек, действуют силы со стороны стыка между крышкой и корпусом редуктора и сила веса 0Кг. Эти силы будем определять в соответствии с расчетной схемой, приведенной на рис.2.13.
При отсутствии контакта между шейками шестеренного валка и крышкой шестеренной клети стяжные шпильки и стык между корпусом и крышкой шестеренной клети нагружены силой предварительной затяжки. При этом шпильки испытывают растяжение, а стык — сжатие. При действии на крышку силы со стороны шестеренного валка крышка смещается вверх. При этом происходит уменьшение контактной силы и увеличение силы растяжения шпилек. При нормальной работе шестеренной клети контактная сила не должна уменьшаться до нуля, то есть стык между крышкой и корпусом шестеренной клети должен оставаться закрытым. Такие условия работы могут быть обеспечены в том случае, если обеспечено необходимое усилие предварительной затяжки, и если моменты прокатки, создающие усилия в зубчатом зацеплении шестеренной клети, не превышают допустимых уровней.
В противном случае контактная сила может уменьшиться до нуля. При этом происходит раскрытие стыка, и вся сила от зубчатого зацепления воспринимается только стяжными шпильками. В результате нагрузка на стяжные шпильки может превысить уровень, при котором происходит пластическая деформация резьбового соединения. При этом после снятия нагрузки с зубчатого зацепления контакт между крышкой и корпусом восстанавливается, но при уменьшенной силе предварительной затяжки. Вследствие уменьшения силы предварительной затяжки в дальнейшем раскрытие стыка может происходить при моментах прокатки, не превышающих допустимый уровень. При этом происходит интенсивный износ контактных поверхностей. На рис.2.15 приведена зависимость суммарной силы Р1КВ, действующей на крышку шестеренной клети в области левого подшипника со стороны двух стяжных шпилек (каждая стяжная шпилька затянут силой Рит ) и контактной поверхности от перемещения х1Кг . На этой схеме показано перемещение хш., при котором происходит раскрытие стыка между корпусом и крышкой шестеренной клети, а также показано перемещение хТЕК, при котором начинаются пластические деформации стяжных шпилек.
В соответствии с этой схемой, при перемещении х1Кг крышки от нуля до величины хш. одновременно с увеличением силы Р1КВ происходит уменьшение контактной силы между крышкой и корпусом и увеличение силы растяжения стяжных шпилек. В этом случае связь между перемещением х\Кг и силой Р1КЙ определятся суммой жесткостей 2(Сет + СЮ1). При нормальном режиме эксплуатации перемещение хАУ должно находиться в пределах 0 х1Кг х/ЛГ. В случае недостаточной величины предварительной затяжки или перегрузки привода величина перемещения х1Кг может превысить величину х т. В результате произойдет раскрытие стыка, и вся нагрузка будет восприниматься стяжными шпильками. В диапазоне хш. х1Кг хТЕК связь между перемещением х1Кг и силой РШ! определятся жесткостью 2СЮ1. В этом диапазоне перемещений нагрузка на стяжные шпильки не превышает нагрузку, при которой происходит пластическая деформация резьбового соединения, и после снятия нагрузки с зубчатого зацепления стык между крышкой и корпусом закроется. Сила предварительной затяжки при этом не изменится. При более высокой степени перегрузки прокатной клети, перемещение х1Кг может превысить величину хТЕК, при которой начинается пластическая деформация резьбы стяжных шпилек. В результате после снятия нагрузки с зубчатого зацепления шестеренных валков разгрузка системы стяжных шпилек и стыка пойдет по пунктирной линии (рис.2.15). В результате сила предварительной затяжки уменьшится до величины Ршп. Это может привести к ситуации, при которой стык будет раскрываться уже при нормальных условиях эксплуатации.