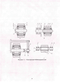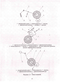Содержание к диссертации
Введение
1 Обзор патентных и литературных источников. Постановка задачи исследования 8
1.1 Обзор конструкций приемно-намоточных механизмов 8
1.2 Обзор литературных источников по исследованию динамики быстровращающихся роторных узлов 28
1.3 Постановка задачи исследования 31
2 Динамические и математические модели приемно- намоточного механизма 33
2.1 Конструктивная схема приемно-намоточного механизма 33
2.2 Динамическая и математическая модели (первыйслучай) 40
2.3 Динамическая и математическая модели (второй случай) 55
3 Исследование динамики приемно-намоточного механизма (первый случай) 70
3.1 Частотный и модальный анализ 70
3.2 Анализ периодических колебательных режимов 78
3.3 Моделирование динамики приемно-намоточного механизма на ЭВМ 97
4 Исследование динамики приемно-намоточного механизма (второй случай) 111
4.1 Частотный, и модальный анализ. Самоцентрирование паковки 111
4.2 Моделирование динамики приемно-намоточного механизма на ЭВМ' 118
Заключение 133
Список использованных источников
- Обзор литературных источников по исследованию динамики быстровращающихся роторных узлов
- Постановка задачи исследования
- Динамическая и математическая модели (первыйслучай)
- Анализ периодических колебательных режимов
Введение к работе
Актуальность темы. Современные условия рынка предъявляют повышенные требования к качеству и себестоимости готовой продукции. Стоимость натурального сырья достаточно высока, а его потребительские свойства, такие как прочность, износостойкость и т. д. оставляют желать лучшего. Поэтому широко внедряются в ассортименты товаров изделия, состоящие из смеси натуральных и химических волокон. Все большее распространение получают текстурированные нити, свойства которых приближаются к свойствам натуральных волокон.
Высокая потребность в химических волокнах и экономическая эффективность их производства обеспечивает постоянное увеличение их сбыта. При этом остро ставится вопрос о повышении качества- и потребительских свойств' химических волокон. Для этой цели разрабатываются новые технологии; совершенствуются существующие и создается новое технологическое оборудование - машины для производства и переработки химических нитей'. Одной из существенных составляющих этих машин, от работы которошзави-сит качество готовой продукции (паковки) являются приемно-намоточные механизмы.
Исходя из сказанного, следует, что работы по разработке новых при-емно-намоточных механизмов, позволяющих наматывать более качественные с точки зрения дальнейших технологических переходов паковки, снизить обрывность наматываемых нитей являются весьма важными и актуальными.
Цели'и задачи исследования. Цель диссертационной работы состоит в аналитическом и численном моделировании* динамики, работы приемно-намоточного механизма, предназначенного для» приемки на патрон'вытянутой, текстурированной полиамидной жгутовой нити коврового ассортимента, снижении их виброактивности, а следовательно, и повышении качества готового продукта - паковок и нити. Исходя из поставленной цели сформулированы следующие задачи исследования:
разработать динамические и соответствующие им математические модели приемно-намоточного механизма машины типа НВ-1000-КЖ9 (разработка СКТБ МХВ ОАО «Машиностроительное объединение им. К. Маркса», г. Санкт-Петербург), учитывающие податливость: элементов, соединяющих подвес с уравновешивающим грузом; опор бобинодержателя; поверхности паковки; неудерживающий характер связи фрикционного цилиндра с паковкой;
проанализировать систему уравновешивания подвеса и в случае необходимости выдать инженерные рекомендации по ее совершенствованию;
выполнить аналитическое исследование периодических колебаний фрикционного цилиндра на подвесе относительно паковки без учета податливости опор бобинодержателя; разработать алгоритмическое и программное обеспечение для построения на ЭВМ резонансных кривых исследуемой- системы;
выполнить частотный и модальный анализ приемно-намоточного механизма для двух случаев: а) опоры бобинодержателя'абсолютно жесткие, б) опоры бобинодержателя податливы; для обоих случаев разработать математические модели, алгоритмическое и программное обеспечение проанализировать в случае б) эффект самоцентрирования патрона с паковкой;
разработать алгоритмическое и программное обеспечение для моделирования на ЭВМ динамики приемно-намоточного механизма (случаи а) и 6)); проанализировать результаты моделирования, выдать инженерные рекомендации по совершенствованию конструкции механизма.
Методы исследования. При выполнении работы применялись методы: математического анализа, теоретической механики, нелинейной механики, математического моделирования, вычислительной математики. При выполнении работы широко использовались возможности современных ЭВМ.
Научная новизна. В процессе выполнения работы получены следующие научные результаты.
Разработана методика исследования динамики и моделирования работы приемно-намоточного механизма намоточной машины типа НВ-1000, существенной частью которых является крепление на рычажном подвесе ни-тераскладчика и фрикционного цилиндра с их электроприводами; при этом бобинодержатель с патроном и паковкой крепится в корпусе машины и представляет собой две конические втулки, на которые одевается патрон.
Разработаны динамические и математические модели намоточного механизма, позволяющие учитывать податливость креплений подвеса с уравновешивающим грузом, податливость паковки, податливость опор бобинодержателя, неудерживающий характер связи между фрикционным цилиндром и паковкой.
Выполнен частотный и модельный анализ приемно-намоточного механизма для двух случаев: а) опоры бобинодержателя абсолютно жесткие, б) опоры бобинодержателя податливые, по разработанному алгоритмическому и программному обеспечению; выявлен при ш -> оо эффект самоцентрирования патрона с паковкой, которым к сожалению по конструктивным особенностям механизма практически невозможно воспользоваться.
Выполнено аналитическое исследование (случай а) периодических колебаний фрикционного цилиндра с нитераскладчиком на подвесе с использованием метода гармонической линеаризации. Построены по разработанному алгоритмическому и программному обеспечению скелетные кривые, линия максимумов, резонансная кривая. Показано, что для получения больших амплитуд колебаний подвеса в резонансных режимах необходимы большие искажения геометрической формы паковки (биение, эллиптичность) и фрикционного ^цилиндра (биение), что практически мало реально, так как при этом резко возрастают силы контактного взаимодействия паковки с фрикционным цилиндром (геометрическая форма паковки при этом должна самокорректироваться из-за укатывания, либо паковка должна разрушаться).
Разработано алгоритмическое и программное обеспечение для численного моделирования динамики приемно-намоточного механизма (случаи
а и б). Выполнен анализ колебаний подвеса с установленным на нем фрикционным цилиндром и нитераскладчиком в зависимости от биения, эллиптичности паковки, биения фрикционного цилиндра; в зависимости от дисбаланса и момента дисбаланса патрона с паковкой; в зависимости от жесткости опор бобинодержателя; в зависимости от жесткостных характеристик элементов, связывающих подвес с уравновешивающим грузом. Показано, что колебания подвеса малы. При этом биение и эллиптичность паковки расти по мере роста радиуса паковки не могут, так как это вызывает резкое увеличение силы контактного взаимодействия паковки с фрикционным цилиндром (поверхность паковки при этом прикатывается).
6. Показано, что необходимо изменение уравновешивания подвеса, так как сила контактного взаимодействия между паковкой и фрикционным цилиндром по мере роста радиуса паковки от 0,035 м до 0,135 м увеличивается< более чем в четыре'раза, что недопустимо из технологических соображений. Даны инженерные рекомендации по устранению данного дефекта как с помощью дополнительного уравновешивающего груза, жестко закрепленного на подвесе, так и с помощью пружины.
Практическая ценность. Разработанные динамические и математические модели, алгоритмическое и программное обеспечение могут быть использованы при проектировании новых и модернизации существующих при-емно-намоточных механизмов текстурирующе-вытяжных машин, войдут составной частью в САПР машин химических волокон СКТБ МХВ ОАО-«Машиностроительное объединение им. К. Маркса», позволят повысить качество паковок и самой текстурированной нити и стабилизации сил контактного взаимодействия между фрикционным цилиндром и паковкой на требуемом уровне, позволят значительно снизить виброактивность механизма.
Теоретические результаты работы, разработанное алгоритмическое и программное обеспечение внедрены в учебный процесс кафедры машиноведения Санкт-Петербургского государственного университета технологии и дизайна в виде разделов курса «Машины и аппараты производства химиче-
ских волокон», «Динамика машин отрасли», в курсовое проектирование указанных курсов, в дипломное проектирование студентов специальности 150600 - «Машины и аппараты текстильной и легкой промышленности»
Апробация работы. Основные положения диссертационной работы были доложены на Всероссийской научно-технической конференции студентов и аспирантов «Проблемы экономики и прогрессивной технологии в текстильной, легкой и полиграфической отраслях промышленности», на конференции «Дни науки - 2007» Санкт-Петербургский государственный университет технологии и дизайна (Санкт-Петербург, 2007), научных семинарах кафедры машиноведения, научном семинаре СКТБ МХВ ОАО «Машиностроительное объединение им. К. Маркса», г. Санкт-Петербург.
Публикации. По теме диссертации опубликовано 3 научных статьи, в том числе 1 статья в журнале, входящем в «Перечань ...» ВАК РФ.
Структура и объем работы. Диссертация состоит из ведения, четырех глав и заключения. Общий объем работы составляет 142 страницы машинописного текста, 55 рисунков, 4 таблицы. Список литературы включает 40 источников.
Обзор литературных источников по исследованию динамики быстровращающихся роторных узлов
Приемно-намоточные механизмы машин для получения и переработки химических волокон и нитей являются типичными представителями широкого класса механизмов, получивших в литературе название высокоскоростные роторные узлы. Перед конструктором роторных систем в подавляющем большинстве случаев.стоит задача повышения частоты.вращения ротора при одновременном снижении массы и габаритных размеров машины. Ограничения на увеличение частоты вращения ротора накладываются прежде всего со стороны динамики, ротора, подшипниковых опор и корпуса машины, в котором установлен ротор: Поэтому динамический расчет высокоскоростных роторных систем является неотъемлемой частью их проектирования.
Впервые ротор с частотой 30000 об/мин, как- оказалось впоследствии превышающей" первую критическую скорость, был сконструирован Лавалем в 1884 г. При экспериментальных исследованиях этого ротора в составе паровой машины-оказалось, что, чемменыие его диаметр;, тем лучше. Теоретическое объяснение этого явления дал Фепль [4], указавший на явление самоцентрирования в роторных узлах. Более подробно и полно теорию гибкого ротора разработал Е.Л.Николем [5]. В основном ими анализировалась динамика гибкого вала с закрепленным на немдиском, вращающегося в абсолютно твердых опорах. Была получена математическая модель рассматриваемой системы, найдены критические скорости, показано, что при стремлении частоты вращения ротора к бесконечности в системе имеет место эффект самоцентрирования, т.е. амплитуды колебаний ротора стремятся к нулю. Был проанализирован гироскопический эффект от насаженного на ротор диска. Авторы не проанализировали влияние на динамику системы внутреннего трения. В настоящее время-проблеме колебаний роторов посвящено множество монографий и публикаций. Например, в работе [6] содержится обзор ранних публикаций, содержащий 554 наименования.
Хотелось бы отметить, что в настоящее время конструкторы при проектировании роторных машин отдают предпочтение не гибким роторам, а жестким роторам, установленным на упругие опоры. Это связано с тем, что гибкие роторы имеют малую прочность; при подходе к зоне самоцентрирования при переходе через критическую скорость возможна потеря устойчивости ротора, вызываемая наличием внутреннего трения.
Одним из основоположников исследования динамики конструирования жестких роторов в 50-х годах XX века являлся А.С.Кельзон [7, 8], его ученики и последователи. Обобщение полученных ими результатов приведено в [4]. Введение упругих опор и жесткого ротора сняло любые ограничения на размеры ротора. В случае необходимости для снижения колебаний ротора в окрестности критических скоростей в упругие опоры вводится демпфирование. При переходе через вторую, третью критическую скорость жесткий ротор, как и гибкий, обладает эффектом самоцентрирования. Этим широко пользуются при проектировании сепараторов и центрифуг различного назначения.
Достаточно подробно имеющиеся в настоящее время работы по динамике быстровращающихся роторных узлов систематизированы и приведены в [4]. Имеются в виду разделы, написанные Э. Л. Поздняком, М. Ф. Зейтма-ном, Я. И. Коритысским, И. А. Биргером, А. Г. Костюком, В. М. Фридманом.
Разделы, написанные М. Ф: Зейтманом и Я. И. Коритысским посвящены колебаниям быстровращающихся роторных узлов текстильных машин, таких как центрифуги, веретена с вертикальным ротором. При их исследовании Я. И. Коритысским предложена теория так называемого "полужесткого" шпинделя, которая более подробно-представлена им в [9, 10]. Теории веретен, автоколебаниям роторных систем посвящена более ранняя работа М. Я. Кушуля [11]. Веретенам же посвящены работы Э. А. Попова [12, 13]. В них проанализирована зависимость динамики веретен от погрешности геометрии подшипниковых опор. Нестационарные режимы колебаний веретен приведены в работах Я. И. Коритысского и его учеников [14, 15, 16], анализируются также колебания тяжелого веретена в массивной опоре, обладающей четырьмя степенями свободы. В исследовании динамики и проектировании мотальных (приемно-намоточных) механизмов с горизонтальным шпинделем большой вклад внес А. Ф. Прошков [2] и его многочисленные ученики А. А. Трощановский [17], А. А. Акимов, В. П. Ильчук [8, 19] и др.
Результаты А. С. Кользона перенес и развил для анализа динамики высокоскоростных бобинодержателей с упругими опорами Е. 3. Регельман [20] и его многочисленные ученики: В. Н. Козлов, Н: В: Рокотов, Е. Е. Бойкова, В: Ф. Мисенко [21 - 24] и т.д. Существенный вклад в исследования динамики высокоскоростных приемно-намоточных механизмов для химических волокон и нитей внес Л. С. Мазин [1, 25]. Им исследовано влияние неудержи-вающей связи паковки с фрикционным цилиндром (прикаточным роликом) на динамику бабинодержателя с патроном и паковкой и фрикционного цилиндра (прикаточного ролика). Показано, в каких случаях возможны отрывы паковки от фрикционного цилиндра, что может привести и к появлению субгармонических колебательных режимов большой амплитуды; выявлена возможность появления в системе параметрических резонансных режимов. Предложены инженерные методы, борьбы с резонансными режимами. Выполненные Л. С. Мазиным и его учениками Т. А. Луганцевой, П. И. Слухаєм, И. М. Беспаловой, К. Цифтесом [25 - 30] и др. Указанные исследования вместе с работами Е. 3. Регельмана и его учеников, А. Ф. Прошкова и его учеников вошли в отраслевые методики для расчета и проектирования машин химических волокон.
Постановка задачи исследования
Рассмотрим приемно-намоточный механизм применительно к намо-точно-вытяжной машине НВ-1000-КЖ9, предназначенной для вытягивания, текстурирования, пневмоперепутывания и намотки на патрон полиамидной жгутовой нити коврового, ассортимента, совмещенной с плавильно-формовочной машиной ПФ1000-КЖ91 в составе агрегата АФС-1000-КЖ9 (разработка СКТБ МХВ ОАО «Машиностроительное объединение им. К. Маркса» совместно-с СПГУТД, г. Санкт-Петербург).
Приемно-намоточный механизм должен наматывать на одном рабочем месте одну нить толщиной (линейной плотностью) 125тексх2, 167тексх2, 250тексх2. Линейная-скорость принимаемой на паковку нити - (22-7-42) м/с. Паковка1 цилиндрическая, крестовой, мотки-, с плоскими торцами. Приемный патрон ПЦГ-59,Зх3004, длина паковки 240 мм, диаметр паковки 270 мм, плотность паковки 0,45 г/см3, масса паковки 6 кг. Фрикционный цилиндр и нитераскладчик имеют собственный индивидуальный электропривод.
Прежде чем рассматривать приемно-намоточный механизм, рассмотрим работу и устройство агрегата АФС-1000-КЖ9. Технологическая схема агрегата приведена на рисунке 2.1.
Объединенная с двух фильерных комплектов в сопроводительной шахте 1 формовочной машины нить проходит мимо сопла стационарного инжектора 2 через паз резательного устройства 3 и щелевые головки замасливающего устройства 4. При этом определенное количество замасливающей жидкости попадает на нить. Далее нить поступает на не обогреваемый цилиндр 5 с раскладывающим роликом б, после чего нить попадает на первый обогреваемый цилиндр 7 с раскладывающим роликом 8 и вторые вытяжные обогреваемые цилиндры 9, заключенные в теплоизоляционный кожух 10.
Вытянутая в два этапа нить поступает в пневмотекстурирующее устройство 11, где нить текстурируется путем запрессовки в виде пыжа в камеру сжатым горячим воздухом. Пыж из пневмотекстурирующего устройства с заданной скоростью выводитсяфифленым роликом 12 и подается на охлаждающее устройство 13. Просасываемый через пыж холодный воздух охлаждает нить, фиксируя образовавшиеся извилины и завитки. Далее нить огибает направляющий ролик 14 и попадает в распрямляющее устройство 75. После распрямляющего устройства, через направляющий ролик 16, нить поступает на первый нагонный цилиндр 77 с раскладывающим роликом 18. Затем нить проходит устройство пневмоперепутывания 19 и поступает на второй нагонный цилиндр 20 с раскладывающим цилиндром 21.
Готовая нить поступает на приемно-намоточный механизм фрикционного типа, состоящий, из нитераскладчика 22 , фрикционного цилиндра 23 и патрона с паковкой 24.
Рассмотрим более подробно конструктивную схему приемно-намоточного механизма, приведенную на рисунке 2.2. На корпусе 7 крепится рычажный подвес 2, на котором установлены нитераскладчик 3 и фрикционный цилиндр 4 с индивидуальными электроприводами. Фрикционный цилиндр вращается с постоянной угловой скоростью со , = const и приводит во вращение патрон с паковкой 5. Так как сила контактного взаимодействия между паковкой и фрикционным цилиндром из технологических соображений ограничена, предусмотрены две системы уравновешивания, подвеса. Во-первых, это пневмоцилиндр 6 и пружина 7, связанные друг с другом тросом, перекинутым через ротор 8. Во-вторых, это груз 9, связанный через трос 10 и ротор 9 с кулачком (отрезок троса АХАА0), выполненным как единое целое с подвесом 7. Патрон с паковкой 5 (также, как патрон 73) крепится на бобино-держателе (на рисунке 2.2 не показан)- не в корпусе машины, а на диске 12, выполненном как единое целое с мальтийским крестом 14. Диск 12 имеет возможность поворачиваться относительно корпуса машины
При полностью намотанной паковке 5 пневмоцилиндр 6 поднимает подвес 2 вверх (точка М занимает положение чуть выше М , соответствующей положению точки Мпри полностью намотанной паковке). При этом подается воздух в пневмоцилиндр 15. Стопор В выходит из диска 12. Электродвигатель через червячную пару поворачивает рычаг с роликом (на рисунке 2.2 не показаны). Ролик входит в паз мальтийского креста и поворачивает диск 12. При этом паковка 5 опускается, а патрон 13 поднимается до тех пор пока не займет положение патрона с паковкой 5. Происходит автоматическая перезаправка нити. Стопор В возвращается на свое место, фиксируя диск 12. Нить начинает наматываться на патрон 13. Одновременно с этим пневмоцилиндр 6 соединяется с атмосферой. Груз 10 перемещает подвес вниз (точка М занимает положение М). Для того, чтобы не произошел удар фрикционного цилиндра 4 о патронУЗ, который встал на место паковки с патроном 5; предусмотрен амортизатор 16.
Рассмотрим теперь более подробно (рисунок 2.3) конструктивную схему бобинодержателей, в которых крепятся-патроны,(см. рисунок 2.2, поз. 5 и 13). Бобинодержатель состоит из двух вращающихся- в опорах качения центров. Передний центр представляет собой пробку 1, закрепленную на валу 2 в подшипниковых опорах 3 относительно корпуса машины 4. Задний вращающийся центр представляет собой пробку 5, закрепленную на валу 6 в подшипниковых опорах 7 в подвижной втулке 8: Втулка 8 может перемещаться в осевом направлении относительно корпуса машины 4. В корпусе машины установлена также втулка 9. Она имеет возможность перемещаться относительно корпуса машины 4 в осевом направлении. Между втулкой 9 и корпусом машины установлена пружина 10, а между втулками 8 и 9 установлены пружины 11. Патон 12, на который наматывается паковка, установлен между двумя вращающимися центрами на пробках 1 и 5
Динамическая и математическая модели (первыйслучай)
Рассмотрим приемно-намоточный механизм, представленный на рисунках 2.2 и 2.3. При рассмотрении первого случая (см. пункт 2.1) примем следующие допущения: - крепление подвеса к корпусу машины; подвес с закрепленными на нем нитераскладчиком и фрикционным цилиндром представляют собой абсолютно твердые тела; - патрон с паковкой, закрепленный в бобинодержателе, представляет собой абсолютно твердое тело; - ротор 8 вместе с его подшипниковыми опорами и груз 9 (см. рисунок 2.2) - абсолютно твердые тела; - жесткость троса, соединяющего пневмоцилиндр б с пружиной 7 (см. рисунок 2.2) значительно выше жесткости элементов б и 7, поэтому данный трос будем считать неподатливым элементом; - отрезки тросов, связывающие груз 9 с ротором 8 и ротор 8 с закрепленном на подвесе кулачком А{А - податливые элементы.
Итак, нами выделены три массивных элемента: подвес с нитераскладчиком и фрикционным цилиндром, ротор 8 и груз 9, которые соединены между собой и с корпусом машины податливыми элементами.
Воспользуемся методом расчленения [33] и представим рассматриваемый приемно-намоточный механизмов виде трех (рисунок 2.4) динамических моделей: динамической модели подвеса (см. рисунок 2.4, а), динамической модели ротора (см. рисунок 2.4, б), динамической модели груза (см. рисунок 2.4, в).
Каждая из указанных моделей имеет одну степень свободы. Введем неподвижные системы координат: OXY (см. рисунок 2.4, а, О - точка качания подвеса), 04XlYlZl (см. рисунок 2.4, б, 04Zj - ось вращения ротора 8) и Cj72 Уг (см. рисунок 2.4, в, ось С,Х3 отсутствует, так как груз движется вдоль оси CXY2, С, - центр тяжести груза). В качестве обобщенных координат выберем: а - угол поворота рычажного подвеса ООх относительно оси ОХ (см. рисунок. 2.4, а); 3 - угол поворота ротора относительно оси 04ZX (см. рисунок 2.4, б); ут - перемещение относительно оси CXY2 уравновешивающего груза (см. рисунок 2.4, в).
Реакции Rx, Rx , (\щ= R{ ),&2- (&г= &г ) соответствуют отброшенным связям (участок троса АХА и трос, связывающий груз 9 с ротором 8); Рп - сила тяжести подвеса с нитераскладчиком и фрикционным цилиндром; Q - сила контактного взаимодействия паковки с фрикционным цилиндром (считаем, что она действует вдоль линии Ох02, соединяющей оси вращения фрикционного цилиндра и паковки); R2 - реакция, соответствующая воздействию на ротор элементов 6 и 7; РГ - сила тяжести уравновешивающего груза; hp, hQ, hR - соответственно плечи сил Рп, Q, Rx; гх, г2, г3 - соответственно радиус ротора, на которых действуют силы R , R2, R3; а, Ъ — координаты точки 02 соответственно по осям OY и ОХ; у — угол между ООх и 002; А-о - угол между ОС и ООх, где С - центр тяжести подвеса в сборе; гк - радиус кулачка подвеса относительно точки О.
Воспользовавшись методом кинетостатики [33] нетрудно получить математическую модель исследуемой системы, соответствующую динамическим моделям (см. рисунок 2.4).
Опустив промежуточные выкладки, запишем: I$ = Rxrx-R2r2+R,r„ (2.1) mryr=-Pr+R2. Система уравнений (2.1) соответствует установочному положению рассматриваемой системы (паковка касается фрикционного цилиндра, О = 0, вращение отсутствует); Іп - приведенный к точке О момент инерции подвеса (см. рисунок 2.4, а); 1р - момент инерции ротора (см. рисунок 2.4, б); а = а0 + ф, где а0 — значение угла а в установочном положении (ос0 = const), ф - отклонение угла а от установочного положения. Запишем аналитические выражения сил, входящих в (2.1). Силу Q контактного взаимодействия паковки с фрикционным цилиндром, имея ввиду малость деформации паковки А вдоль линии действия силы Q, запишем в виде: Q0, при А 0 и 0о О, Q = (2.2) О при А 0 либо Q0 0, J Q0 = cnA + bnVn, где сп, Ьп - соответственно приведенные жесткость и коэффициент сопротивления поверхности паковки; Vn — скорость деформации паковки вдоль линии действия силы Q, А 0 соответствует отрыву паковки от фрикционного цилиндра.
Для того чтобы разобраться в скорости Vn обратимся к рисунку 2.5.
Пусть О,, 02 - соответственно оси вращения фрикционного цилиндра и "паковки", R,, Rn -радиусы фрикционного цилиндра и "паковки", А1В1 -характеризует ширину пятна касания фрикционного цилиндра и "паковки" при деформации последней на величину А.
Введем систему координат 02ху, ось 02у которой совпадает с линией Ох02. Непосредственно из рисунка 2.5 видно, что Кп=А + и, где A = dA/dt, о - скорость деформации радиуса 02АУ до 02А2 в пятне касания перед тем, как радиус 02А{ окажется на линии Ох02, что связано с непрерывным вращением фрикционного цилиндра и "паковки".
Анализ периодических колебательных режимов
Для анализа периодических колебательных режимов приемно-намоточного механизма (см. рисунок 2.2) воспользуемся математической моделью (2.1). Данная математическая модель является сугубо нелинейной. Для анализа ее периодических колебательных режимов воспользуемся методом гармонической линеаризации. В первом приближении будем считать, что участки канатов, соответствующие силам Rt, і = 1,2 не провисают. В таком случае (2.1) примет вид:
В выражениях (3.24), (3.25) неизвестными, определяемыми из (3.22) являются f0, q, г, поэтому найти решения (3.25), (3.24) можно лишь с помощью ЭВМ. Нас больше всего интересуют колебания "паковки" относительно фрикционного цилиндра, то есть А{, так как именно от них зависит качество наматываемой на патрон паковки. Поэтому ниже в основном будем анализировать именно их. Построим зависимость А2 = А2 (зз). — fzero(fun, [x1 x2]) - возвращает значения x, при которых fun(x)=0 с заданием интервала поиска с помощью вектора Х=[х1 х2]; — fft(x) — возвращает для вектора X дискретное преобразование Фурье, по возможности используя алгоритм быстрого преобразование Фурье; если х матрица, функция fft(x) возвращает преобразование Фурье для каждого столбца матрицы; — Iinspace(a, b, n) - возвращает линейный массив из п строк, равномерно распределенных между а и Ь; — length(t) - возвращает количество элементов массива t Соответствие переменных в тексте и в программе приведено в таблице 3.1 (см. пункт 3.1).
Перейдем к описанию алгоритма счета (см. рисунок 3.3). В блоках 2 и 3 осуществляется описание глобальных переменных и счет вспомогательных переменных, необходимых для работы программы.
Построение скелетной кривой, линии максимумов и амплитудно-частотной характеристики осуществляется путем задания амплитуды dltl (блок 4) и последовательного вычисления4 методом перебора по известной величине невязок: dltO (блоки 5, 6, 7); частот wsk(k), соответствующих точкам скелетной кривой (блоки 8 - 18); частот w1max(k), соответствующих точкам линии максимумов (блоки 19 - 30); частот wach(k, kk), соответствующих точкам амплитудно-частотной характеристики (блоки 31 - 46). Блок 47 осуществляет печать результатов счета в плоскости (dIt"1, w). Печатаются при известном dltl (задается в начале счета) точки, соответствующие частотам, которые принадлежат скелетной кривой, линии максимумов и амплитудно-частотной характеристике: function [fO, q, г] = garlin(dlt0, dltl) - служит для определения коэффициентов гармонической линеаризации ГО, q, г момента Q-hq; function Q = silaQ(dltO, dltl) - служит для вычисления Q-hq; function epsl = neveps1(dlt0, dltl) - служит для вычисления невязки (необходима для работы fzero()) при определении dltO при заданном dltl; function nevw = skeletk1(wt, dltO, dltl) - служит для вычисления невязки (необходима для работы fzero()) при вычислении частот, соответствующих скелетным кривым, при заданных dltO, dltl; function nev = ndmax(wt, dltO, dltl) - служит для вычисления невязки (необходима для работы fzero()) при вычислении частот, соответствующих линии максимумов, при заданных dltO, dltl; function nev = nach(wt, dltO, dltl) - служит для вычисления невязки (необходима для работы fzero()) при вычислении частот, соответствующих амплитудно-частотной характеристике, при заданных dltO, dltl; function dd = coeff(a, wt) - промежуточная функция, необходимая для определения d(i, j) при работе обеих функций nev при известных a(i, j).
Результат счета приведен на рисунке 3.4. Для удобства восприятия результат счета приведен в виде трех участков оси абсцисс со, т.е. [0,50] с-1, [700,800] с-1, [1200,1400] с-1 расположенных-последовательно друг за другом. Резонансные частоты существенно зависят от величин сп, с, и с2 (см. пункт 3.1). Результаты счета (см. рисунок 3.4) соответствуют случаю сп =5-105 Н/м, С! =6-106 Н/м и с2 =8-106 Н/м. Изменение величин С , с, и с2 приводит к сдвигу скелетных кривых вдоль оси абсцисс, но качественной картины не меняют, поэтому отсутствуют ниже. Как следует из результатов счета по мере увеличения величины JAJ] (ТО есть роста величин отрывов фрикционного цилиндра паковки) скелетная кривая 1 (см. рисунок 3.4) сдвигается влево. При значительном уменьшении масштабов графиков в областях [700,800] с-1 и [1200,1400] с-1 можно отметить аналогичный сдвиг влево скелетных кривых Г и 7", но он мал и им практически можно пренебречь. Линия максимумов 2 пересекает скелетную кривую 1 в точке А и резко опускается вниз стремясь к оси абсцисс.