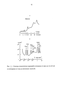Содержание к диссертации
Введение
Глава 1. Обзор. 8
1.1. Структура магнитного поля Земли. 8
1.2. Методы измерения магнитного поля . 14
Глава 2. Методика обработки геомагнитных данных. 20
2.1. Введение. 20
2.2. Исследование погрешностей моделей, полученных методом сферического гармонического анализа . 27
2.3. Метод естественных ортогональных составляющих,
использующийся для обработки обсерваторских и спутниковых данных. 37
Глава 3. Моделирование геомагнитного поля по данным мировой сети обсерваторий. 41
3.1. Введение. 41
3.2. Данные. 42
3.3. Разделение геомагнитного поля по пространственно-временному признаку . 48
3.3.1. Разделение поля по суточным данным. 48
3.3.2. Разделение поля по часовым данным. 54
3.3.3. Разделение поля по минутным данным. 58
Глава 4. Моделирование геомагнитного поля по данным спутников . 70
4.1. Введение. 70
4.2. Данные. 73
4.3. Среднесуточные модели главного геомагнитного поля . 75
4.4. Выводы. 90
Глава 5. Разделение магнитного поля по пространственному признаку . 91
5.1. Разделение магнитного поля на внутреннее и внешнее для тел, имеющих форму вытянутого сфероида. 91
5.1.1. Введение. 91
5.1.2. Разделение полей с помощью интегралов типа Коши. 94
5.1.3. Разделение поля для тел, имеющих форму вытянутого сфероида . 100
5.1.4. Система координат вытянутого сфероида. 101
5.1.5. Решение уравнения Лапласа в системе координат вытянутого сфероида. 103
5.1.6. Разделение поля на поверхности сфероида на внешнее и внутреннее. 106
5.2. Представление магнитного поля в виде суммы диполей. 108
5.2.1 Введение. 108
5.2.2. Связь параметров произвольного диполя и коэффициентов сферического гармонического анализа в задачах моделирования магнитного поля Земли. ПО
5.2.3. Выводы. 116
Заключение. 117
Список литературы.
- Исследование погрешностей моделей, полученных методом сферического гармонического анализа
- Разделение геомагнитного поля по пространственно-временному признаку
- Среднесуточные модели главного геомагнитного поля
- Разделение поля для тел, имеющих форму вытянутого сфероида
Введение к работе
Актуальность проблемы.
Генерация магнитного поля Земли является одной из важнейших проблем физики (генерация магнитного поля в природе), одной из проблем геофизики (процессы внутри Земли, приводящие к генерации ее магнитного поля) и одной из проблем солнечно-земной физики (взаимодействие солнечного ветра с магнитосферой Земли).
Изучение геомагнитного поля начинается с измерения его величины во времени и пространстве. Измеренное поле содержит вклад поля, генерируемого в жидком ядре Земли, поля намагниченности ферритосодержащих горных пород, полей, генерируемых в магнитосфере и ионосфере Земли, индукционных полей в электропроводящих оболочках Земли и т.п. Для изучения каждого из этих полей необходимо разработать методы разделения данных измерений на части различной природы. Эта задача является наиболее актуальной в современной магнитометрии.
Следующим шагом является построение пространственно-временных моделей каждого из источников поля, поскольку только такие модели позволяют решать обратную задачу - исследование физических процессов генерации каждого вида источников. Таким образом, моделирование поля также является актуальной задачей.
Поскольку представленная работа посвящена решению задач разделения измеренных полей и их пространственно-временному моделированию, она является актуальной.
Цель работы.
Целью работы является: разработка новых и модификация известных методов обработки данных для построения моделей отдельных вариаций поля, которые бы соответствовали объемам и точности современных данных геомагнитных измерений за последнее десятилетие;
создание пространственно-временных моделей магнитного поля Земли по данным обсерваторий и по спутниковым данным, дающих возможность изучения его морфологии;
создание нового алгоритма измерений магнитного поля на носителях, имеющих собственное магнитное поле.
Основные положения диссертации, выносимые на защиту.
1. Результаты разделения геомагнитного поля по данным мировой сети
обсерваторий, позволившие построить пространственно - временные модели
геомагнитного поля день ото дня для интервалов (1964-65), (1990-91) и (1999-2000)
годов.
Оригинальная методика обработки спутниковых данных, которая дает возможность оптимальным образом рассчитать модели главного геомагнитного поля и его вековой вариации.
Модель главного геомагнитного поля и его вековой вариации по данным спутника CHAMP для интервала времени с 01.05.2001 по 30.01.07.
4. Алгоритм разделения магнитного поля для объекта, имеющего форму
вытянутого сфероида, на внутреннюю и внешнюю части, позволяющий определить
его динамическую девиацию.
5. Формулы связи сферических гармонических коэффициентов с параметрами
произвольно расположенного внутри Земли диполя, дающие возможность решать
обратную задачу нахождения параметров диполя по сферическим гармоническим
моделям.
Научная новизна и практическая значимость работы.
Впервые для анализа данных магнитных обсерваторий с временами от минут до суток были выполнены разложения по методу естественных ортогональных составляющих и получены пространственно-временные модели геомагнитных вариаций в этом диапазоне времен.
Разработан новый метод обработки данных спутниковых магнитных съемок для построения модели главного геомагнитного поля и его вековой вариации. На его основе были получены прогностические модели, которые были предложены в
качестве моделей-кандидатов для создания международной модели IGRF MF-2005 и IGRF SV-2007.5.
- Впервые разработан алгоритм разделения магнитного поля для объектов,
имеющих форму вытянутого сфероида, с целью определения его динамической
девиации. Он лег в основу проекта, по которому получен грант РФФИ по
Целевым Ориентированным Фундаментальным Исследованиям.
- Практическая значимость диссертации состоит, в частности, в том, что при
использовании полученных автором среднесуточных гармонических моделей
можно резко увеличить количество дней с повышенной геомагнитной
активностью, в которые возможно выполнять качественные геомагнитные съемки.
Эти модели используются для выделения аномальной компоненты геомагнитного
поля. В качестве примера можно привести обработку данных полета
стратосферного аэростата с магнитометрами на борту в октябре 2003 года на
следующий день после прохождения большой магнитной бури. Восстановить
уровень геомагнитного поля, относительно которого было выделено аномальное
геомагнитное поле, удалось только с использованием разработанной по методике
автора диссертации модели.
Результаты исследования погрешностей моделей СГА позволили оптимизировать сеть морских измерений для экспедиции ЛО ИЗМИРАН.
Вывод формул связи сферических гармонических коэффициентов с параметрами произвольного диполя был включен Смолиным СВ. в курс лекций для студентов кафедры геофизики Красноярского университета.
Личный вклад автора.
В полном объеме автором была выполнена обработка обсерваторских и спутниковых данных и построены по ним пространственно-временные модели геомагнитного поля. Автор самостоятельно разработал алгоритм разделения магнитного поля, измеренного на поверхности тела, имеющего форму вытянутого эллипсоида вращения, на внутреннюю и внешнюю части. Им самостоятельно получены формулы связи сферических гармонических коэффициентов с параметрами произвольно расположенного внутри Земли диполя.
Работа была поддержана грантами РФФИ №№ 03-05-64518 и
7 06-05-64598, aTaocelNTAS 01-0142, MHTU,KR-214.
Апробация работы и публикации.
Основные результаты работы докладывались на международных конференциях:
Научная Ассамблея IAGA, Uppsala, 1997;
Международная конференция по спутникам OERSTED и CHAMP, Копенгаген, Дания, 2002;
Международная конференция "Проблемы геокосмоса", Санкт-Петербург, 2004;
Международная конференция по спутнику CHAMP, Потсдам, Германия. 2004, 2005;
Генеральная ассамблея Европейского Геофизического Союза, Вена, Австрия, 2005:
Научная Ассамблея IAGA, Тулуза, Франция, 2005;
Европейский Симпозиум по баллонным исследованием, Sandefjord, Норвегия, 2005;
Международная Ассамблея IUGG, Перуджа, Италия, 2007.
По теме диссертации опубликовано 15 научных работ.
Структура и объем диссертации.
Диссертация состоит из введения, 5 глав, заключения и списка литературы, содержит 126 страниц, из них 30 рисунков и 10 таблиц. Список литературы включает 102 наименования.
Благодарности. Автор выражает благодарность В.П.Головкову за научное руководство; В.ЕЛевитину, Л.И.Громовой и С.П.Гайдашу за обсуждение идей и недостатков данной работы; Т.Н.Бондарь, С.В.Филиппову за сотрудничество; Л.И.Яковлевой и Н.И.Волковой за помощь при оформлении; других сотрудников отдела за поддержку.
Исследование погрешностей моделей, полученных методом сферического гармонического анализа
Метод сферического гармонического анализа - один из методов, используемый в данной работе, развивается с середины позапрошлого века. Исходя из предположения, что магнитное поле потенциально, потенциал главного магнитного поля можно представить в виде разложения по сферическим функциям [Яновский, 1978]: N п fa\n + l m л , цт п.,пШ, и(г,0Д) = а- II- (gmcosm?t + hmsiniTU)xPm(cose) (2_1) п = 1т = (А n n п Х--1 Y = L ; Z = - -, (2 2) г d0 rsinG dX dr где U - геомагнитный потенциал в точке с географическими координатами г, 9, X; X,Y и Z представляют собой северную, восточную и вертикальную, направленную вниз, компоненты поля; а - средний радиус Земли; P"(cos 9) - присоединенные функции Лежандра степени п и порядка m в нормировке Шмидта; g и h постоянные коэффициенты.
В ранних анализах число искомых коэффициентов не превышало 24 (п=4), в настоящее время с помощью современных компьютеров считаются модели с числом гармоник n=720 [Мат, http://models.geomag.us/index.htmf]. Совершенствование метода шло по многим направлениям; использовались в анализах не только "линейные" компоненты X,Y,Z, но и H,T,D,I; разделялись поля на внутреннюю и внешнюю части, учитывалась изменяемость поля во времени путем рассмотрения искомых коэффициентов как функций, зависящих от времени, и т.д. Но во всех анализах важным аспектом был и остается вопрос точности полученной модели. Этой проблеме посвящено огромное количество работ, которые появляются и по сей день по причине важности ее решения. Вот только некоторые из них [Langel R.,1980; Lowes F.J., 1975; Barker F.S., 1985; Головков, 1989]. Источниками ошибок получаемых сферических гармонических коэффициентов являются погрешности исходных измерений, обрезание ряда разложения поля по сферическим функциям, неравномерность данных в пространстве и во времени, степень переопределенности системы условных уравнений в методе наименьших квадратов, которая определяется как отношение числа условных уравнений к порядку нормальной системы уравнений. При увеличении порядка модели, частично уменьшается ошибка сферических коэффициентов за счет обрезания ряда, но остаются ошибки за счет других факторов.
Ошибки в сферических коэффициентах в зависимости от количества исходных измерений. Рассмотрим зависимость решения нормальной системы уравнений, полученной методом наименьших квадратов, от степени переопределенности начальной системы условных уравнений. Данные считаются равномерно распределенными по земному шару, в анализах участвуют в качестве экспериментальных данных Х-, Y-, Z- компоненты поля. Предполагается, что данные некоррелированы и имеют дисперсию ad. В случае идеально расположенных данных (т.е. их много и они равномерно распределены в пространстве) некоррелированность означает, что ковариационная матрица ошибок исходных данных имеет вид Vd = adI, где /-единичная матрица.
Матрица весовых коэффициентов имеет вид W{ll a2d)l и, следовательно, результирующая ковариационная матрица сферических гармонических коэффициентов упростится V (A WAr a A)- , где А - матрица системы исходных уравнений в традиционном методе взвешенных наименьших квадратов. Для идеально расположенных данных матрица (АТА) так же, как и обратная к ней, являются диагональными со значениями на диагоналях N(n+1) и l/(N(n+l)) соответственно, где п- порядок соответствующего сферического коэффициента, а N - число точек измерений (каждая точка представлена измерениями Х-, Y-, Z- компонент). Дисперсия сферических коэффициентов в этом случае представляет собой C= /(N(N + 1)). (2_3)
Заметим, что a2sgc в идеальном случае не зависит от т. В реальных анализах такая оценка отличается от действительных ошибок. Ошибки в получаемых моделях возникают по разным причинам (основные из них были названы выше) и тесно взаимосвязаны между собой. Нельзя учесть все причины ошибок одновременно, поэтому приходится рассматривать какой-либо один источник ошибок, абстрагируясь от остальных. Как ведет себя ошибка в сферических коэффициентах для различной переопределенности системы, показывают результаты следующего теста. Были просчитаны сферические анализы для различных наборов равномерно распределенных в пространстве данных. Порядок моделей во всех анализах брался п=5, т.е. число искомых сферических коэффициентов равнялось 35. В качестве исходных измерений использовались синтезированные данные по равномерным сеткам. Количество исходных данных бралось везде равным, а именно таким, чтобы переопределенность системы составляла 3,5,8,10,15,20. Сетки в различных наборах данных были разными, но шаг по широте везде равнялся шагу по долготе. Во всех сферических анализах к синтезированным данным добавлялась ошибка, равномерно распределенная на интервале (-1000,1000) нТл. После проделанных сферических анализов сравнивались исходные и полученные сферические гармонические коэффициенты по среднеквадратичному отклонению и по максимуму модуля разности по всем коэффициентам. Из табл. 2_1 видна динамика уменьшения ошибок с ростом переопределенности системы условных уравнений. Кроме того, возможно оценить ту степень переопределенности, которую необходимо иметь для достижения требуемой точности модели.
Разделение геомагнитного поля по пространственно-временному признаку
Как уже говорилось, по обсерваторским данным были исследованы несколько двухлетних интервалов суточных компонентных измерений, соответствующих различным моментам 11- летнего цикла солнечной активности: интервал, соответствующий минимуму солнечного цикла (1964-65гг), высокой (1990-91гг) и средней солнечной активности (1999-2000гг).
Представленные рисунки 3_2 содержат три временных составляющих Ті, Т2, Тз при разложении совместно Х- и Z- компонент поля методом ЕОС для перечисленных временных интервалов и для обсерваторий из табл.3_1.
(Здесь и далее обозначения Ti=Tl, Т2=Т2,...., Si=Sl и т.д. в тексте и на рисунках). По оси абсцисс отложено время в днях, а по оси ординат - величина Т\ -функций в условных единицах.
Следует особо подчеркнуть, что величина разделяемых вариаций в нТл и их знак получаются после умножения значения Т-функции в данный момент времени на значение S-функции в данной точке (см. раздел 2.3). Программа метода ЕОС сконструирована таким образом, что меньший номер Т-функции присваивается той из них, у которой большая величина дисперсии. Это свойство программы следует учитывать при сравнении результатов анализа временных рядов различных компонент поля. Также следует учитывать, что для удобства сравнения в программе выполняется нормирование таким образом, что значения пространственных составляющих Sy (S- имя компоненты, kj - ее номер) лежат в пределах (-1,+1). Таким образом, масштаб ординат различных Т-функций качественно отражает их вклад в описание вариаций поля по всей сети обсерваторий.
Из графиков на рисунках 3_2 видно, что для всех трех временных интервалов первая временная составляющая Ті описывает вековой ход, вторая Тг - магнитную активность, а третья Т3 - сезонные изменения магнитного поля.
Рядом с каждой кривой Тк всех рисунков приведено значение в процентах, качественно определяющее вклад данного вида вариаций в исходное поле. Указанная величина определялась как DT Р(о/0) = —L. юо, где DD Do ZBi/, DTk=ETik2ZSik2 , i=l j=l i=l j=l By- - измеряемые компоненты X,Y,Z магнитного поля. Очевидно, что полный вклад может быть определен из условия min[IJ] DD= EDTk+De, k где De- сумма квадратов ошибок в данных. Однако, как правило, разложение методом ЕОС ограничивалось первыми тремя-пятью Тк (к 5). Ограничение min[IJ] длины ряда определялось условием Д « De, где А = ] DTk . к=К
Таким образом, для интервала 1964-65гг. первая составляющая в ряду разложения по методу ЕОС "выбирает" аппроксимируемое поле на 90.5%, вторая - на 6.6%, а на третью приходится всего 0.6%. Для интервала 1990-91гг. аналогичные цифры равны 67%, 30% и 1.5%. Для интервала 1999-2000гг. те же цифры равны 71.3%, 25.3% и 1.4%.
Для анализов по другим компонентам и наборам компонент, а также для других временных интервалов выделяются аналогичные три составляющих, но их вклад в аппроксимируемое поле различен. Так, например, для интервала 1990-91гг. в анализе только по Z-компоненте (EOCZ) первая составляющая представляет собой вековой ход и "выбирает" поле на 96%, вторая - описывает магнитную активность (3%), годовая вариация в третьей составляющей составляет 0.3%. Анализ только по Х-компоненте (ЕОСХ) дает картину несколько иную: первая составляющая описывает магнитную активность (87%), вторая - вековой ход (13%), третья -годовую вариацию (3%). В Х-компоненте годовая вариация выделяется лучше, чем в Z-компоненте, что подтверждает выводы работы [Courtillot & Le Mouel, 1988].
Для выяснения природы вариации, описывающей магнитную активность, временная составляющая Т2 (для интервала 1990-91гг.) была сопоставлена с ходом среднесуточных значений Dst- индекса. Коэффициент корреляции между этими кривыми оказался равным 0,97. Глобальный характер Т2 подтверждается следующими соображениями: если рассмотреть рис. 3_3, на котором значения соответствующей пространственной составляющей S2 представлены в зависимости от широты каждой обсерватории, то хорошо видно, что вторая пространственная гармоника S2 соответствует косинусоидальной зависимости от широты. Все это дает основания уверенно идентифицировать вторую временную составляюшую Т2 как Dst-вариацию, что справедливо и для остальных двух интервалов.
Что касается третьей временной составляющей, во всех ЕОС-анализах она представляет собой годовую вариацию, и про нее можно сказать следующее. Во-первых, она устойчиво выделяется во всех анализах, хотя величина ее мала (ее относительный вклад в поле не более 3%). Во-вторых, очевидно, что источник ее пространственно не связан с Dst - вариацией, а именно, с кольцевым током и с токами на границе магнитосферы (условие ортогональности). В третьих, для различных интервалов времени ее фаза остается постоянной.
Среднесуточные модели главного геомагнитного поля
Пространственное распределение вариаций на поверхности Земли (исключая высокие широты) было получено разложением по сферическим гармоникам каждой пространственной естественной ортогональной составляющей отдельно по формулам (2_2) раздела 2_2.
Учитывая, с одной стороны, необходимость более или менее равномерного покрытия поверхности Земли данными, а с другой стороны, необходимость иметь переопределенную систему условных уравнений для получения статистически обоснованных коэффициентов, был выполнен анализ методом EOCXYZ по данным 25 средне и низкоширотных обсерваторий (75 условных уравнений), что позволило получить разложение до степени и порядка п=3. Коэффициенты разложения представлены в таблице 3_5.
Из этой таблицы видно, что пространственное распределение Ті среднеширотного набора данных соответствует полю наклонного диполя с полюсом, близким к геомагнитному. Для Т2 и Т3 наборы коэффициентов показывают большой вклад недипольной составляющей, причем позиция максимума горизонтальной составляющей смещена в высокие широты. Недостаточно высокая степень разложения и отсутствие в исходных данных обсерваторий высоких широт не позволяют получить для Т2 и Т3 адекватную модель их распределения в пространстве, но тем не менее, очевидно, что это распределение не соответствует полю центрального диполя, перпендикулярного магнитной оси Земли. Таким образом, из всестороннего анализа естественных ортогональных составляющих следует, что Ті соответствует полю Dst-вариации, а Т2 и Т3 производятся возмущениями высокоширотной ионосферы.
Фундаментальным результатом проведенного исследования следует считать быструю сходимость ряда ЕОС для анализа средне и низкоширотных данных. Быстрая сходимость свидетельствует о том, что используемый метод адекватен данным и позволяет разделить их таким образом, что каждой временной составляющей Т соответствует физически независимый источник вариаций в магнитосфере или ионосфере Земли. По существу, не считая регулярных Sq вариаций, было выделено всего два таких источника. Это, во-первых, кольцевой ток и токи на границе магнитосферы, описываемые функцией Tj и соответственно индексом Dst. Во-вторых, это высокоширотные возмущения, описываемые Т2 и Т3, которые, как следует из рис.3_7 и табл.3_5, имеют примерно одинаковую дисперсию и степень недипольности в пространственном распределении. Тем не менее метод ЕОС выделяет их в разные составляющие. Формальной причиной такого разделения является их некоррелированность в пространстве и во времени. Это указывает на то, что начало и главная фаза каждой из этих вариаций приурочены к разным геомагнитным долготам, что характерно для авроральных возмущений.
Заключительным этапом исследования было разложение по методу ЕОС одноминутных значений. Большой объем данных заставил нас сократить длину выборки, и мы ограничились 18 часами (1080 значений в строке матрицы Щ в формуле (2_4). Временные отрезки такой длительности выбирались внутри бури (27-30.07.90), там, где по 6-минутным значениям мы наблюдали наиболее резкие изменения (на рис. 3_7 эти интервалы обозначены сверху, а по горизонтальной оси 2-й, например, интервал соответствует точкам с 42 по 58).
На рис. 3_10-3_12 представлены 3 разложения серий 1-минутных значений. Длина серий составляла 18 часов, причем первый интервал предшествовал буре (с 4 до 22 часов мирового времени 27 июля 1990г.). Развитие бури описывается двумя следующими 18-часовыми интервалами. Рисунки 3_10-3_12 позволяют полностью оценить возможности метода как с точки зрения его алгебры, так и физики вариаций.
Во-первых, смысл Т] оказался различным для интервалов 1, 2, 3. Для интервалов 2 и 3 Т описывает глобальное возмущение, коррелирующее с Dst-индексом. Хорошо видно, что переход от часовых к 6-минутным и далее к минутным значениям не изменяет вид вариации, а лишь растягивает ее во времени. А для первого интервала одноминутная Tj соответствует Т2 6-минутного и Т2 одноминутного - Т3 6-минутного. Таким образом, на этом временном интервале преобладают вариации, производимые S-токовой системой в ионосфере. Что касается Тк, описывающих S-вариацию, видно, что независимо от к переход час, 6-минут, минута также не изменяет форму кривых. Возмущения этих Тк, возникшие во время бури, также принципиально не изменяются с изменением временного масштаба серий.
Из сказанного выше можно заключить, что изменение масштаба не приводит к выявлению новых, независимых видов вариаций. Это подтверждают и две дополнительные временные функции Т4 и Т5, приведенные на рис.3_12 (3-ий интервал). Хорошо видно, что в их ходе присутствуют все основные особенности, описанные Т2 и Тз. Причина такого взаимопроникновения вариаций в разные Т обусловлена алгеброй метода. Математический аппарат разделяет вариации, удовлетворяя условию ортогональности абсолютно. Однако, физическое различие токовых систем создает полностью ортогональные в пространстве структуры поля только интегрально на всей поверхности Земли. Расположение сети обсерваторий в средних широтах приводит к тому, что на данном наборе точек в пространстве поля физически разных источников могут частично коррелировать. В этом случае взаимокоррелирующая часть этих полей будет включена программой в одну временную функцию. Очевидно, что поля высокочастотных токовых систем могут частично коррелировать с полями суточных вариаций (возмущения в Ті и Т2 всех масштабов осреднения).
Разделение поля для тел, имеющих форму вытянутого сфероида
При решении уравнения Лапласа в случае, когда краевая функция задается на поверхностях, имеющих форму вытянутого эллипсоида вращения, удобно использовать систему координат вытянутого эллипсоида (или, как ее обычно называют, вытянутого сфероида). Эта система координат является ортогональной, т.е. соответствующие ей координатные поверхности пересекаются под прямыми углами; другими словами, касательные к координатным линиям в любой точке на поверхности сфероида будут перпендикулярны друг другу.
Система координат вытянутого сфероида определяется тремя переменными r\,Z,,(?. Их связь с прямоугольными декартовыми координатами выглядит следующим образом (ось Z - ось вращения):
Таким образом, рассматривая решение уравнения Лапласа в системе координат вытянутого сфероида, удалось решить задачу разделения магнитных полей объектов, имеющих форму вытянутых эллипсоидов вращения, на внешнее и внутреннее, не касаясь их природы. Использование теории сфероидальных функций открывает возможность решить ряд задач магнитометрии, а именно: задачу учета магнитной девиации; задачу оптимизации системы магнитных измерений путем нахождения сети точек на поверхности сфероидального объекта, на которой выполнены условия ортогональности полиномов Лежандра.
Также результаты вышеописанной работы могут найти применение в широком круге задач магнитной навигации и магнитной картографии.
Для изучения постоянного магнитного поля Земли обычно используется представление потенциала поля U в виде сферического гармонического ряда Гаусса. Это очень распространено и удобно, так как, имея набор коэффициентов, можно по известным формулам посчитать поле в любой точке на поверхности Земли. Известен основной недостаток этой модели - ее формальный характер.
Существуют и другие модели магнитного поля, например, представление поля суммой нескольких диполей или токовых петель и др. Зная параметры диполей (или токовых петель), можно получить поле в любой точке Земли. Эта модель физична и, как показано, например, в работах [Бочев,1969; Зидаров, 1969], описывает магнитное поле не хуже и меньшим числом параметров. Основная трудность представления поля дипольной моделью состоит в отыскании оптимальных параметров диполей.
В этом направлении существует много работ. Для того, чтобы найти параметры одного эксцентричного диполя, были использованы различные приближения [Bartels,1936; Winch, 1968; James, 1970]. Олдридж и др. [Alldredge,1964] аппроксимировали поле одним центральным и несколькими радиальными диполями. Случай двух и трех азимутальных диполей рассмотрен Ляховым [Ляхов, 1960,1963]. [Зидаров и Бочев,1965,1969] дали общую постановку задачи о представлении поля суммой нескольких произвольных диполей, заданных декартовыми координатами, и привели численные расчеты для двух и трех диполей.
Параметры диполей ищутся путем минимизации целевой функции, представляющей собой среднеквадратичное отклонение измеренного магнитного поля от модельного. Трудности определения параметров в большой степени зависят от вида целевой функции. В случае, когда она рассматривается как функция декартовых координат (как в работах [Зидаров, 1965,1969]), она имеет сложный вид. Целевая функция значительно упрощается, если рассматривать ее, а также задавать диполи в сферических координатах. С таким подходом решались задачи Калининым [Калинин, 1963,1969] и Ляховым [Ляхов,I960,1963]. Калинин выводит связь СГК с параметрами диполя с помощью последовательных преобразований координат. Магнитный момент диполя он задает в локальной системе с помощью углов. [Winch ,1968] и [James, 1970] дают связь сферических гармонических коэффициентов (СГК) с параметрами мультиполя любого порядка.
В данной работе приводится в явном виде связь СГК с параметрами произвольного диполя, заданного в сферических координатах [Зверева 1982]. Необходимость этого вызвана тем, что в качестве экспериментальных данных в процессе минимизации целевой функции нередко бывает необходимым использовать не значения магнитного поля, а СГК. Кроме того, с помощью СГК можно вычислять пространственные энергетические спектры поля (вычислять энергию, которую несет в себе каждая гармоника поля), генерируемого источником геомагнитного поля в виде набора диполей.