Управление режимами активно – адаптивных электрических сетей на основе моделирования и параметрической идентификации узлов нагрузки Ле Зань Конг

Содержание к диссертации

Введение

1. Методы моделирования узлов нагрузки 11

1.1. Описание объекта управления и постановка задач исследований 11

1.2. Традиционные модели нагрузки электроэнергетических систем 18

1.3. Статические характеристики нагрузки 23

1.4. Графики электрических нагрузок 53

Выводы 59

2. Модели элементов электроэнергетических систем в фазных координатах 62

2.1. Моделирование многопроводных элементов в фазных координатах 62

2.2. Уравнения установившегося режима, записанные на основе фазных координат 65

2.3. Моделирование нагрузок в фазных координатах 74

Выводы 78

3. Моделирование асинхронной нагрузки 79

3.1. Основные положения моделирования 79

3.2. Алгоритм определения параметров модели

3.2.1. Параметры схемы номинального режима 80

3.2.2. Параметры пускового режима 83

3.2.3. Влияние характеристик механизма на режим двигателя 84

3.2.4. Работа АЭД при несимметричном питании

3.3. Алгоритм определения параметров модели двигателя на итерациях 92

3.4. Примеры расчета статической характеристики АЭД 94

Выводы 104

4. Учет стационарных нагрузок в задачах моделирования и управления режимами систем электроснабжения железных дорог 106

4.1. Симметрирующий эффект асинхронной нагрузки 106

4.2. Учет АН при моделировании режимов систем электроснабжения железных дорог 113

4.3. Учет динамики изменения нагрузок при имитационном моделировании СЭЖД 117

4.4. Примеры учета АН в задачах моделирования и управления 120

4.4.1. Влияние коэффициента загрузки на симметрирующий эффект асинхронного электродвигателя 121

4.4.2. Деформация статических характеристик асинхронной нагрузки при несимметрии напряжения питающей сети 124

4.4.3. Влияние асинхронной нагрузки на уровень потерь мощности в электрической сети 128

4.5. Учет нелинейных нагрузок 131

4.6. Управление режимами на основе концепции активного потребителя 140

Выводы 145

5. Параметрическая идентификация узлов нагрузки 147

5.1. Задачи идентификации узлов нагрузки 147

5.2. Обзор существующих методов параметрической идентификации асинхронных электродвигателей 152

5.3. Методика параметрической идентификации асинхронной нагрузки 155

5.4. Идентификация узлов нагрузки, включающих электроприводы, оборудованные СПЧ 164

Выводы 172

Заключение 174

Библиографический список 176

• Традиционные модели нагрузки электроэнергетических систем
• Уравнения установившегося режима, записанные на основе фазных координат
• Параметры схемы номинального режима
• Примеры учета АН в задачах моделирования и управления

Введение к работе

Актуальность темы диссертационных исследований. В электрических сетях могут иметь место сложнонесимметричные режимы, возникающие из-за наличия большого числа однофазных электроприемников, неравномерно распределенных по фазам. В наибольшей степени такие режимы проявляются в сетях, питающихся от районных обмоток тяговых трансформаторов железных дорог переменного тока. Поэтому задача снижения уровней несимметрии в таких сетях приобретает особую актуальность. Для корректного решения этой задачи необходимы методы анализа сложнонесимметричных режимов электроэнергетических систем (ЭЭС). Следует отметить важность корректного учета узлов нагрузки при расчете таких режимов. Прежде всего это касается асинхронной нагрузки (АН), так как асинхронные электродвигатели могут создавать симметрирующий эффект из-за неравенства сопротивлений прямой и обратной последовательностей. Несмотря на наличие работ, посвященных вопросам учета нагрузки при расчетах нормальных и аварийных режимов электрических сетей, вопрос количественной оценки симметрирующего эффекта асинхронной нагрузки изучен недостаточно.

Современный этап развития электроэнергетики России характеризуется переходом на технологическую платформу, основанную на концепции интеллектуальных энергосистем с активно-адаптивными электрическими сетями (smart grid). Реализация этой концепции невозможна без разработки новых подходов, обеспечивающих более эффективное решение задач управления технологическими процессами выработки, передачи, распределения и, особенно, потребления электрической энергии. Для практической реализации таких подходов также необходимы эффективные методы моделирования режимов ЭЭС. Они должны обеспечивать высокую точность, которая может быть достигнута на основе адекватных математических моделей элементов ЭЭС и низких погрешностей исходных данных.

Значительный вклад в решение проблемы создания технологий активно-адаптивных сетей внесли О.М. Бударгин, В.Н. Вариводов, Н.И. Воропай, В.В. Дорофеев, Т.В. Иванов, С.Н. Иванов, Б.Б. Кобец, В.Г. Курбацкий, Ю.Н. Кучеров, Е.И. Логинов, А.А. Макаров, М.Ш. Мисриханов, Ю.И. Моржин, Э.Б. Наумов, В.Н.

Рябченко, В.Н. Седунов, В.Ф. Ситников, В.А. Скопинцев, Ю.Г. Шакарян, М. Donnelly, C.W. Gelling, J.M. Guerrero Zapata, N.D. Hatziargyriou, S.A. Papathanassiou, J.A. Pecas Lopes. J. Schmid, Z. Styczynski, и другие.

Значения параметров элементов ЭЭС, обладающие приемлемой для целей управления режимами ЭЭС точностью, могут быть получены на основе методов параметрической идентификации. Теоретические основы и алгоритмы идентификации представлены в работах Н.М. Александровского, А.А. Бессонова, A.M. Дейча, А.Н. Дмитриева, Н.Н. Карабутова, Льюнга Л. С.Н. Музыкина, И.И. Перельмана, И.В. Прангишвили, Н.С. Райбмана, Э.П. Сейджа, В.В. Солодовникова, ЯЗ. Цыпкина, П Эйхскоффа. и других. Разработанные в общей теории идентификации алгоритмы в основном касаются динамических моделей систем управления и потому их применение для идентификации элементов ЭЭС в задачах моделирования стационарных режимов является проблематичным. В работах Лордкипанидзе В.Д., Файбисовича В.А., Шелюга С.Н. представлены методы идентификации силовых элементов электроэнергетических систем, основанные на однолинейном представлении схем замещения, которые сложно применять для определения режимов при наличии продольной и поперечной несимметрии. Более эффективные методы идентификации элементов ЭЭС, использующие фазные координаты, предложены в работах ИрГУПСа. Однако они предназначены только для нахождения параметров линий электропередачи и трансформаторов на основе результатов измерений. Вопросы идентификации узлов нагрузки в этих работах не рассматриваются.

Для решения вопросов управления режимами ИЭСС ААС кроме моделей ЛЭП и трансформаторов необходимы адекватные модели узлов нагрузки. Причем особое значение имеют задачи моделирования и идентификации асинхронной нагрузки, которая в промышленных узлах может быть преобладающей. Повышенную актуальность вопросы моделирования узлов нагрузки приобретают при использовании концепции активных потребителей, участвующих в управлении режимами ИЭЭС ААС.

Вопросам моделирования асинхронной нагрузки в однолинейной постановке, затрудняющей решение задач моделирования несимметричных режимов, посвящены работы Гуревича Ю.Е., Либовой Л.Е., Хачатряна Э.А.

Перечисленные выше работы создают методологический базис для решения задач моделирования и параметрической идентификации узлов асинхронной нагрузки.

Целью диссертационной работы является разработка методов моделирования и параметрической идентификации узлов нагрузки ЭЭС для решения задач управления несимметричными режимами интеллектуальных электроэнергетических систем с активно-адаптивными сетями.

Достижение сформулированной цели возможно на основе решения следующих задач:

1. разработать метод моделирования узлов комплексной нагрузки в фазных координатах, включающих стационарные компоненты (электрическое освещение, нагревательные установки, устройства компенсации реактивной мощности) и асинхронные электродвигатели;

2. разработать метод параметрической идентификации узлов нагрузки в фазных координатах;

3. предложить методику идентификации узлов асинхронной нагрузки, включающей в свой состав электроприводы, оснащенные статическими преобразователями частоты;

4. решить задачу моделирования несинусоидальных режимов, возникающих при наличии частотно-регулируемых приводов.

Объект исследований. Узлы комплексной нагрузки интеллектуальных электроэнергетических систем с активно-адаптивными сетями (smart grid).

Предмет исследований. Методы моделирования и параметрической идентификации узлов комплексной нагрузки ИЭЭС ААС.

Методы исследования. Задачи диссертационного исследования решались на основе математического моделирования электроэнергетических систем с использованием аппарата функционального анализа и численных методов решения нелинейных уравнений большой размерности. Вычислительные эксперименты были проведены на основе пакета SimPowerSystem MatLab и программного комплекса «Fazonord», разработанного в ИрГУПСе и модернизированного в части реализации алгоритмов параметрической идентификации узлов нагрузки ЭЭС.

Научная новизна состоит в том, что в диссертации впервые получены следующие положения, которые выносятся на защиту:

5. разработан метод моделирования узлов комплексной нагрузки в фазных координатах, отличающийся от известных применением фазных координат и применимый в задачах управления режимами интеллектуальных электроэнергетических систем с активно-адаптивными сетями;

6. разработан метод параметрической идентификации узлов нагрузки в фазных координатах, применимый в задачах управления режимами интеллектуальных электроэнергетических систем с активно-адаптивными сетями и отличающийся от известных структурой модели в виде трех источников токов с параметрами, уточняемыми в процессе итерационного расчета режимов ЭЭС;

7. предложена оригинальная методика идентификации узлов асинхронной нагрузки, включающей в свой состав электроприводы, оснащенные статическими преобразователями частоты, применимая в задачах управления режимами ИЭСС ААС;

8. получено решение задачи моделирования несинусоидальных режимов, возникающих при наличии частотно-регулируемых приводов, отличающееся от известных алгоритмом, построенным на основе фазных координат и применимое в задачах управления режимами ИЭЭС ААС.

Достоверность результатов, представленных в диссертации, обоснована корректным применением математических методов и алгоритмов. В сопоставимых случаях выполнено сравнение результатов моделирования узлов нагрузки с данными, полученными с помощью промышленных программ.

Теоретическая и практическая значимость. Разработана методология моделирования и параметрической идентификации узлов нагрузки в фазных координатах, которая может применяться при решении научно-технических задач, связанных с управлением режимами интеллектуальных электроэнергетических систем с активно-адаптивными сетями.

С помощью предложенных в диссертации идентификационных моделей асинхронной нагрузки можно решать следующие практические задачи управления режимами ИЭЭС ААС:

увеличение точности моделирования режимов;

б

обоснованный выбор мероприятий по снижению несимметрии в электрических сетях с учетом симметрирующего эффекта асинхронной нагрузки.

Реализация результатов работы. Результаты моделирования конкретных узлов комплексной нагрузки и практические рекомендации по устранению несимметрии с учетом симметрирующего эффекта АН использованы в научно-технических разработках центра «Параметр». Материалы диссертации используются в учебном процессе на кафедрах «Электроэнергетика транспорта» ИрГУПСа и «Электроснабжение и электротехника» ИрГТУ.

На основе программного комплекса «Fazonord» и разработанных в диссертации моделей комплексной нагрузки выполнены расчеты несимметричных режимов питающих сетей города Нья Чанг Социалистической Республики Вьетнам.

Апробация работы. Научные результаты, полученные в процессе диссертационных исследований, обсуждались на международных научно-практических конференциях «Транспортная инфраструктура Сибирского региона» (Иркутск, 2012, 2013, 2014 и 2015 гг.); всероссийских научно-практических конференциях с международным участием «Повышение эффективности производства и использования электроэнергии в условиях Сибири» (Иркутск, 2012, 2013, 2014, 2015 гг.); XVIII и XIX Байкальских всероссийских конференциях (Иркутск, 2013, 2014 гг.); IV международной научно-технической конференции «Электроэнергетика глазами молодежи» (Новочеркасск, 2013 г.); XVII Межвузовской научно - технической конференции студентов и магистрантов «Молодая мысль - развитию энергетики» (Братск, 2014).

Публикации. Результаты исследований опубликованы в 23 работах, из них 7 статей в рецензируемых изданиях, рекомендованных ВАК РФ, и одна монография. В работах, которые опубликованы с соавторами, автору диссертации принадлежит от 30 до 75 % результатов. Положения, которые определяют научную новизну и выносятся на защиту, получены автором лично.

Объём и структура диссертации. Диссертация включает следующие разделы: введение, четыре главы основного текста, заключение, библиографический список из 170 наименований. Объем диссертации 187 страниц, в тексте содержится 171 рисунков и 32 таблиц.

В процессе диссертационных исследований автор пользовался научными консультациями доктора технических наук, профессора Закарюкина В.П.

Традиционные модели нагрузки электроэнергетических систем

Электроэнергетическая система представляет собой совокупность электростанций, электрических сетей и потребителей электроэнергии, соединенных между собой и связанных общностью режима в непрерывном процессе производства, преобразования и распределения электрической энергии при общем управлении этим режимом.

Электрическая энергия, выработанная в генерирующих устройствах, передается по линиям электропередачи и распределяется электрическими сетями между потребителями. Потребители электрической энергии состоят из групп электроприемников, представляющих собой аппараты, агрегаты, механизмы, предназначенные для преобразования ЭЭ в другие виды энергии.

Потребители электроэнергии различаются по составу электроприемников и режимам их работы. К основным потребителям ЭЭ относятся промышленные предприятия, объекты коммунально-бытовой и социально-культурной сферы, электрифицированный транспорт, сельскохозяйственные потребители и другие.

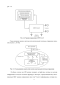
При анализе режимов ЭЭС рассматриваются узлы нагрузки, то есть группы нагрузок, присоединенных к мощной подстанции, кольцу ЛЭП или отдельной линии электропередачи высокого напряжения и т.д. (рис. 1.4). В состав этих групп могут включаться также синхронные компенсаторы или синхронные генераторы небольшой мощности, входящие в системы распределенной генерации [94].

Состав потребителей, присоединенных к узлу нагрузки, может меняться в довольно широких пределах. Средние цифры [9], характеризующие подстанцию, питающую город, приведены в табл. 1.1.

Различные способы представления нагрузки: а) эквивалентная нагрузка, подключенная к сети высокого напряжения; б) нагрузка на шинах 35 и 10 кВ; в) развернутая схема узла нагрузки; АЭД - асинхронные двигатели; СД - синхронные двигатели; ЭУ - электротехнологическая установка; ЭО - электрическое освещение; БК - батарея конденсаторов

Одним из самых распространенных электроприемников является асинхронные двигатели. Они различаются по номинальной мощности, всегда потребляют реактивные токи и могут работать при разных значениях cos q в зависимости от загрузки. Синхронные двигатели могут не только потреблять, но и генерировать реактивную мощность. Современная коммунально-бытовая нагрузка кроме освещения (лампы накаливания, люминесцентные и светодиодные светильники) может включать в свой состав широкий спектр различных электроприемников. Значительная часть современных электробытовых приборов имеет нелинейные воль-тамперные характеристики.

Потребление электроэнергии на бытовые нужды имеет тенденцию к росту вследствие увеличения числа двигателей (пылесосы, полотеры, стиральные машины, электробритвы), а также телевизоров, персональных компьютеров кондиционеров, холодильников. Все это приводит к росту реактивной мощности коммунально-бытовой нагрузки [25]. Растет удельный вес специальных видов промышленной нагрузки: выпрямителей и инверторов, электрохимии и электрометаллургии, например электролизной нагрузки и дуговых сталеплавильных печей, электрифицированного железнодорожного и городского транспорта. Существенную часть от потребления электроэнергии составляют потери в сетях.

В широко применяемых методах расчета режимов ЭЭС используется однолинейное представление трехфазных цепей и используются следующие модели узлов нагрузки:

Модели в виде неизменных отборов мощности обычно использоваться в узлах, имеющих средства регулирования напряжения, например, регулируемые источники реактивной мощности. Модели, реализованные как сопротивления, можно применять для моделирования коммунально-бытовой нагрузки. Источниками тока часто задаются тяговые нагрузки [151]. При наличии достоверной информа ции о составе и режимах работы узла нагрузки наиболее корректной является модель в виде статических характеристик.

Мощности нагрузки изменяются при вариациях напряжения, и потому модели по схемам, представленным на рис. 1.5а, 1.56, 1.5в, являются приближенными. Анализ показывает, что значения 7 н и Ін изменяются при вариациях [/(рис. 1.6 и 1.7). Наибольшие отклонения параметров Z_H, /яот величин, вычисленных при U = UHOM, наблюдается при снижениях напряжения. Поэтому моделирование нагрузки токами или сопротивлениями (проводимостями) может сопровождаться заметными погрешностями при расчетах режимов, которые характеризуются значительными снижениями напряжения. Степень соответствия модели в виде источника тока реальной нагрузке возрастает для сетей с малыми изменениями напряжений и небольшими фазовыми углами

В сетях напряжением до 35 кВ значения напряжений находятся в достаточно узких пределах по модулю и практически совпадают по фазе. Фазовые сдвиги векторов напряжений 8 не превышают 1...2 градусов. Поэтому форма представления нагрузок в виде источников тока с неизменными модулями и фазами дает удовлетворительные результаты. Представление нагрузки сопротивлениями при квадратичной зависимости от напряжения не обеспечивает высокой точности результатов расчета режима, но для определенного состава нагрузок погрешность моделирования может лежать в допустимых пределах.

Под характеристиками нагрузки понимают зависимости потребляемых активной и реактивной мощностей, вращающего момента или тока от напряжения или частоты. Различают два вида характеристик нагрузки - статические и динамические.

Статической характеристикой называется зависимость мощности, момента или тока от напряжения [/(или частоты/), определенная при настолько медленных изменениях режима, что каждую её точку можно считать соответствующей установившемуся режиму. Статическая характеристика представляется в виде кривой или группы кривых на плоскости, например, Рн = Рн(и), Рн = PH{f) Динамической характеристикой называется аналогичная зависимость, но определенная при таких изменениях режима, скорость протекания которых должна быть учтена. Динамическая характеристика представляется в виде зависимости какого-либо показателя, характеризующего нагрузку, от одного или нескольких параметров режима ЭЭС и их производных. Например

Порядок преобразования схем замещения базируется на представлении асинхронного двигателя как вращающегося трансформатора [19]. Значения сопротивлений Х1 и Х2 соответствует номинальной частоте. Коэффициент транс Е формации, который при s = \, т.е. при ш = 0, равен - - (рис. 1.15а), определяется Е2 витковыми данными машины. В обмотке статора протекает ток 1Х частоты /0 = 50 Гц, в роторе - ток 12 частоты sf0, результирующее поле машины вращает ся с синхронной частотой f0. Электродвижущая сила в обмотке ротора пропорциональна частоте тока ротора и при номинальной частоте сети равна E2s. При s = О (синхронный режим) поле статора не пересекает витки ротора и Е2 = 12 = О. Индуктивное сопротивление рассеяния равно sX2.

Для упрощения схемы замещения ЭДС обмотки ротора Е2 и ее сопротивление R2 + jsX2 делят на s, при этом токи 1Х и 12 не изменяются. Тогда схема замещения, показанная на рис. 1.15а преобразуется в схему обычного трансформатора (рис. 1.156). Из-за различия числа витков статора и ротора ЭДС Ех и Е2 не равны, поэтому последнюю схему удобно заменить такой, в которой число витков статора и ротора равны. Режим статора при этом не изменяется, но сопротивления об R R мотки ротора становятся другими: — - + jX2 вместо — + jX2 (рис. 1.15в). При S S равенстве ЭДС обмоток этой схеме эквивалентна схема замещения, показанная на рис. 1.15г, в которой X - сопротивление ветви намагничивания. В упрощенных расчетах сопротивление X , которое много больше, чем Zx = R1 + jX1, выносят на зажимы машины и получают Г-образную схему замещения. Активным сопротивлением ротора в расчетах режимов обычно пренебрегают. При этом вносится некоторая погрешность, проанализированная ниже.

Уравнения установившегося режима, записанные на основе фазных координат

Однолинейные модели ЭЭС, широко применяемые до настоящего времени, были предложены в прошлом веке. Они основаны на ряде допущений, что было связано с отсутствием средств, обеспечивающих решение задач большой размерности. Развитие однолинейных моделей и их применение для решения задач управления ИЭЭС вряд ли оправданно.

Модели, реализованные в фазных координатах, отвечают наиболее адекватному описанию многофазных ЭЭС, характеризующихся заметной продольной и поперечной несимметрией. Такие модели могут быть сформированы на основе решетчатых схем замещения из активных, индуктивных и емкостных элементов, которые соединяются по схемам полных графов (рис. 2.1).

Решетчатая схема замещения для ЛЭП, исходная схема которой показана на рис. 2.2, может быть получена в следующем порядке.

Формируется матрица проводимостей РСЗ (размерностью п=2г) без учета емкостных связей между проводами, а также между проводами и землей: матрица сопротивлений, имеющая размерность rxr; zik = zki; г полное число проводов ЛЭП; М0 - матрица, которая определяется с помощью

С помощью обратной матрицы В =А-1 можно найти собственные и взаимные частичные емкости и определить шунты, сопротивления которых определяются половиной собственной емкости. Эти шунты добавляются в узлы РСЗ. Также с каждой стороны модели ЛЭП формируются ветви с сопротивлениями, которые рассчитываются по половинным значениям взаимных емкостей.

Для трансформаторов матрица РСЗ формируется на основе следующего соотношения: матрица, элементы которой представляют собой электрические сопротивления обмоток; RM- матрица, составленная из магнитных сопротивлений; Wl5 W2 - матрицы, включающие числа витков обмоток [87].

На основе схемы соединений обмоток можно преобразовать матрицу Ypc. Такое преобразование отвечает объединению соответствующих узлов и сложению образующихся при этом параллельных ветвей РСЗ и может быть проиллюстрировано следующим образом. Если число объединяемых узлов равно к и они имеют последние номера, то матрицу YPC можно разделить на блоки:

С помощью матриц Ysk, к = \...п, отдельных элементов ЭЭС формируется модель сети, пример графического представления которой, сформированного средствами программного комплекса Fazonord, показан на рис. 2.5.

Процесс формирования модели ЭЭС в фазных координатах, которой отвечает матрица проводимостей Yz, можно проиллюстрировать на примере схемы, приведенной на рис. 2.6. Матрицу Yz можно получить так: где X - вектор зависимых переменных, включающий составляющие узловых напряжений в декартовой \U k,Ul) или полярной \Uk,Sk) системах координат (рис. 2.7); Y - вектор независимых переменных, состоящий из активных и реак Здесь и в дальнейшем под U подразумеваются фазные напряжения, поэтому для упрощения записи нижний индекс «F» опускается. тивных мощностей генераторов и нагрузок.

Двухполюсники нагрузок, которые включаются между узлами к и j, представлены такими же моделями, но СХН становятся более сложными, так как требуется учет модуля разности напряжений между узлами: где верхний знак отвечает направлению стрелки ИТ от узла к, второй - в узел к. В обозначениях индексов приняты следующие обозначения: номера ветви, следующие первыми, определяют величины, связанные с ветвью, например, SkiIT означает сопряженный поток мощности из узла к в ветвь, имеющей источник тока; номера узлов, стоящие на втором месте, отвечают величине, отнесенной к элементу, имеющимися в ветви; например, QkiIRM - это поток мощности в ветвь с ИРМ, a QIRMki - это реактивная мощность ИРМ, подключенному в ветви Та. Правые части уравнений (2.5) определяются в декартовых координатах следующим образом:

Параметры схемы номинального режима

В соответствии со спецификой сети, питающейся от районной обмотки тягового трансформатора, несимметрия в схему вводилась двумя способами: путем задания несимметричных напряжений источника питания; при этом напряжение прямой последовательности принималось неизменным, а напряжение обратной последовательности представлялась в виде стационарного случайного процесса, определяемого соотношением UC2(t) = C1, где k2U - коэффициент несимметрии по обратной последовательности, %; математическое ожидание М(к2и) принято равным 5, а дисперсия - D(k2U) = 0.2M(k2U); с помощью подключения к приемному концу ЛЭП трех однофазных элек троприемников разной мощности с сопротивлениями ZHA = ZH; Zm = kZH; ZLHC =ZH\ к = 0.2.

Из-за наличия разных по величине нагрузок фаз схема является несимметричной, что затрудняет применение метода симметричных составляющих. Для преодоления этого затруднения можно использовать прием, описанный в работе [66]. Его суть состоит в замене несимметричной нагрузки тремя источниками неизвестных напряжений UA, UB, UC.B результате схема становится симметричной (рис. 4.4), и в ней имеются источники несимметричных напряжений и ЭДС.

Разложив напряжения и ЭДС на симметричные составляющие, можно по 108 лучить схему, в которой на ответвлении, где была нагрузка, находятся источники трех симметричных составляющих. Для выполнения расчета несимметричного режима при включенном двигателе составляются схемы замещения прямой, обратной и нулевой последовательностей и определяются их параметры.

Если двигатель отключен, то расчет выполняется по описанной выше методике, за исключением того, что эквивалентные сопротивления прямой и обратной последовательностей определяются по следующим формулам: Z-ЕІ = ZLC\ + Z-LI Z-E2 = Z-C2 + ZLL Коэффициент несимметрии по обратной последовательности определяется

Динамика изменения коэффициента к2и Коэффициент несимметрии по обратной последовательности, %

Анализ результатов моделирования дает возможность сделать вывод, о том, что наличие асинхронной нагрузки приводит к заметному снижению несимметрии. Средне значение к2и уменьшается на 65 %, а максимум - на 42 %.

Таким образом, за счет симметрирующего эффекта АЭД уровень несимметрии может быть значительно снижен (в расчетном примере более чем на 60 %).

В качестве второго примера определения симметрирующего эффекта АН на по основе фазных координат рассмотрена схема электрической сети, питающейся от источника несимметричного напряжения, по рис. 4.6. К шинам 10 кВ подключалась комплексная нагрузка в следующем составе:

Расчеты выполнялись для трех вариантов представления комплексной нагрузки. В первом варианте промышленная нагрузка представлялась эквивалентным асинхронным двигателем; коммунально-бытовая - сопротивлениями 76+/43 Ом на фазу; нагрузка, не зависящая от уровня напряжений - неизменными нагрузки отборами мощности. В третьем варианте весь узел моделировался комплексными сопротивлениями. Полученные результаты проиллюстрированы на

Таким образом, анализ моделей узлов нагрузки, применяемых при расчете режимов электроэнергетических систем, показал, что при наличии узлов промышленной нагрузки следует использовать модели в виде эквивалентных асинхронных электродвигателей. Использование упрощенных моделей в виде отборов мощности или сопротивлений может привести к существенному завышению уровней несимметрии из-за неучета симметрирующего эффекта асинхронной нагрузки. 4.2. Учет АН при моделировании режимов систем электроснабжения железных дорог Исследование влияния асинхронной нагрузки на режим работы системы тягового электроснабжения проводилось на основе моделирования реальной СТЭ, принципиальная схема которой представлена на рис. 4.11, а схема расчетной модели ПК Fazonord в фазных координатах, сформированной средствами этого комплекса, показана на рис. 4.12.

В состав СЭЖД входят три сложных подсистемы: внешняя сеть ЭЭС, СТЭ и РЭС, которые активно взаимодействуют друг с другом. Вследствие этого неучет вариаций нагрузок ЭЭС и РЭС может приводит к появлению заметных погрешностей имитационного моделирования режимов СТЭ. Для иллюстрации этого факта выполнено моделирование СЭЖД, схемы которой представлены на рис. 4.19, 4.20. Продольный профиль участка ЖД приведен на рис. 4.21. Токовый профиль показан на рис. 4.22. Графики тяговых и нетяговых нагрузок представлены на рис. 4.23 и 4.24. Схема расчетной модели показана на рис. 4.25.

Правильный учет узлов нагрузки особенно актуален при расчете несимметричных режимов. Прежде всего это касается асинхронной нагрузки, так как доля асинхронных электродвигателей в узлах промышленной нагрузки достаточно велика. Несмотря на наличие работ, посвященных учету нагрузки при расчетах режимов и устойчивости ЭЭС [17... 19], вопросы моделирования нагрузки при несимметричном питании изучены не в полной мере. В настоящем разделе представлены результаты моделирования СХН асинхронного электродвигателя при наличии несимметрии питающего напряжения.

Примеры учета АН в задачах моделирования и управления

Полученное значение X необходимо умножить на базисное сопротивление, определяемое по номинальным параметрам АЭД. Исходная информация в виде модулей и углов тока и напряжения, а также скольжения формировалась на основе компьютерного моделирования с помощью программного комплекса Fazonord [38]. Для этого в программном комплексе была создана схема замещения АЭД номинальной мощностью 90 кВт. В полученные токи и напряжения рассчитанного режима вводились погрешности, отвечающие классам точности измерительных приборов 0.1, 0.2, 0.5 и 1. Сопротивление X вычислялось на основе выражения (5.3).

Результаты идентификации представлены на рис. 5.6. Параметр R2 определялся с погрешностью, близкой к нулю. Полученные результаты показывают, что для получения приемлемой точности идентификации следует использовать измерительные средства с классом точности, обеспечивающим максимальную погрешность не более 0.2 %.

Предложенная методика может использоваться для решения задачи параметрической идентификации группы АЭД, подключенной к узловой точке электрической сети. Для подтверждения этой возможности выполнена идентификация узла АН, схема которого показана на рис. 5.7. Параметры АЭД сведены в табл.

Примечания: SUx, 81x - погрешности по модулям напряжений и токов, %; 8 ри , 8(pI -погрешности по фазам напряжений и токов, мин; 8Р, 8Q - погрешности по активной и реактивной мощностям, потребляемым узлом АН, %; SAPL, 8AQL- погрешности по потерям активной и реактивной мощности в питающей ЛЭП; 8к2и- погрешность по коэффициенту несимметрии.

В табл. 5.4 и на рис. 5.12 и 5.13 представлены статические характеристики Р = P(UPH ), Q = Q(UPH ) где Р, Q - активные и реактивные мощности, потребляемые узлом АН; Uт - фазное напряжение. Эти зависимости построены для исходной и эквивалентной моделей узла АН. Анализ результатов моделирования дает возможность сделать вывод о том, что модель узла АН, сформированная на основе параметрической идентификации, позволяет корректно моделировать узел асинхронной нагрузки в широком диапазоне изменения режимов работы сети.

Таким образом, с помощью параметрической идентификации можно получить эквивалентную модель узла асинхронной нагрузки, обеспечивающую высокую точность расчетов как симметричных, так и несимметричных режимов. При этом необходимо особо отметить корректную работу модели в широком диапазоне изменения режимных параметров.

Предложенная методика адекватно работает и для схем узлов АН более общего вида, модели которых показана на рис. 5.14, 5.15. В этих схемах асинхронные двигатели подключены к шинам узла через кабельные линии. Кроме того, питание узла осуществлялось с помощью шинопровода ШМА4, для моделирования которого использовалась методика, описанная в работе [53].

Результаты моделирования представлены в табл. 5.5, из которой видно, что эквивалентные модели, имеющие структуру, аналогичную представленной на рис. 5.8, обеспечивает приемлемую точность расчета несимметричных режимов.

Полученные результаты позволяют сделать следующие выводы. 1. Методика параметрической идентификации узлов асинхронной нагрузки позволяет получить адекватные модели АЭД, обеспечивающие высокую точность определения несимметричных режимов; в рассмотренном расчетном примере погрешность расчета модулей напряжений фаз при различных схемах подключения двигателей не превышает 1.5 %. 2. При наличии в узле статической нагрузки погрешность эквивалентной модели увеличивается; в расчетном примере при доле стационарной нагрузки 75 % величина погрешности определения модулей напряжений увеличивалась до 5 %, а токов - до 3.3 %. 5.4. Идентификация узлов нагрузки, включающих электроприводы, оборудованные СПЧ На современных производствах широко применяются регулируемые асинхронные электроприводы, оснащенные статическими преобразователями частоты [148]. Поэтому становится актуальной задача идентификации узлов АН, содержащих наряду с обычными АЭД частотно-регулируемые асинхронные электроприводы.

Проверка адекватности и точности предложенной методики идентификации при наличии в узле нагрузки электроприводов, оснащенных СПЧ, проводилась следующим образом. На основе пакета SymPowerSy stems системы Matlab была сформирована модель узла нагрузки, схема которой приведена на рис. 5.18. Мощность АЭД, регулируемого СПЧ, была принята равной 22 кВт. Мощность нерегулируемого АЭД варьировалась в пределах от 22 кВт до 90 кВт. Соотношение мощностей задавалось коэффициентом где Р h - активная мощность, потребляемая из сети частотно-регулируемым приводом; Paed - мощность, потребляемая нерегулируемым АЭД. Питание СЭС осуществлялось от источника с несимметричным напряжением, что соответствует реальным условиям, имеющим место для многих объектов, подключенных к районным обмоткам тяговых подстанций железных дорог. Результаты, полученные на основе моделирования, представлены в табл. 5.6.